C# 求俩个正整数的最小公倍数和最大公约数

C# 求俩个正整数的最小公倍数和最大公约数

1.公倍数、最小公倍数

两个或多个整数公有的倍数叫做它们的公倍数，其中除0以外最小的一个公倍数就叫做这几个整数的最小公倍数

翻开小学5年级下册PPT

1.1介绍

常用办法

1、列举法

   例如：求6和8的最小公倍数。

   6的倍数有：6，12，18，24，30，36，42，48，……

   8的倍数有：8，16，24，32，40，48，……

   6和8的公倍数：24，48，……其中24是6和8的最小公倍数。

   这种方法是先分别写出各自的倍数，再找出它们的公倍数，然后在公倍数里找出它们的最小公倍数。

2、分解质因数法。

   我们也可以利用分解质因数的方法，比较简便地求出两个数的最小公倍数。

   例如：求60和42的最小公倍数。

60=2×2×3×5   42=2×3×7

60和42的最小公倍数=2×3×2×5×7=420 。

这种方法是把60和42分别质因数后，观察相同的质因数只取一个（如2，3），把各自独有的质因数全部乘进去，所得的积就是这两个数的最小公倍数。

3、短除法。

  用短除法求18和24的最小公倍数。

2      18      24     …………先同时除以公因数2

    3   9      12    …………再同时除以公因数3

        3       4    ……除到两个商只有公因数1为止。

把所有的除数和最后的两个商连乘，得到：18和24的最小公倍数是2×3×3×4＝72，可表示为[18,24]＝2×3×3×4＝72。

用短除法求两个数的最小公倍数，一般都用这两个数除以它们的公因数，一直除到所得的两个商只有公因数1为止。把所有的除数和最后的两个商连乘起来，就得到这两个数的最小公倍数。

 

 

2.公约数、最大公约数

2.1介绍

公约数，亦称“公因数”。它是一个能被若干个整数同时均整除的整数。如果一个整数同时是几个整数的约数，称这个整数为它们的“公约数”；公约数中最大的称为最大公约数。

翻开小学5年级下册PPT 约数和公约数，最大公约数

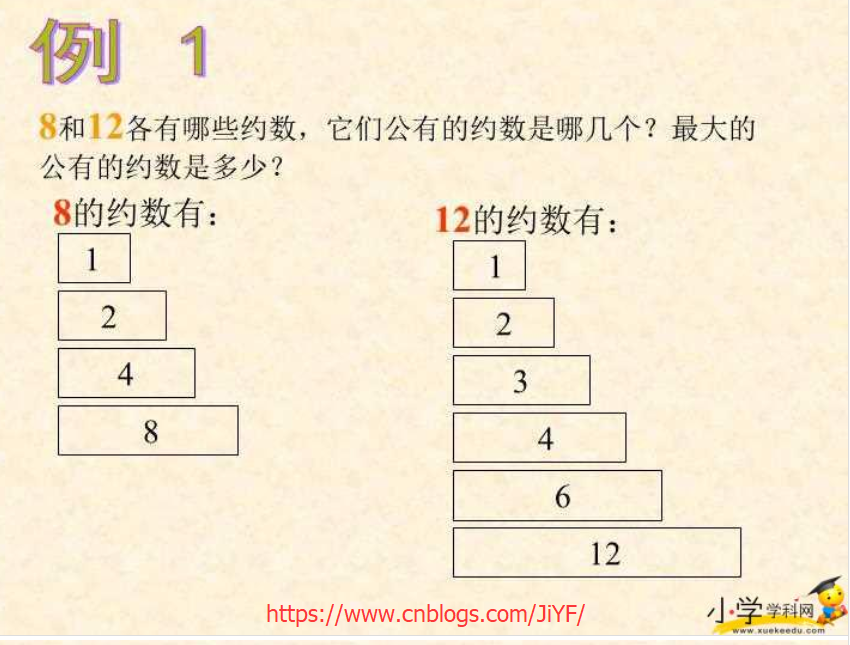
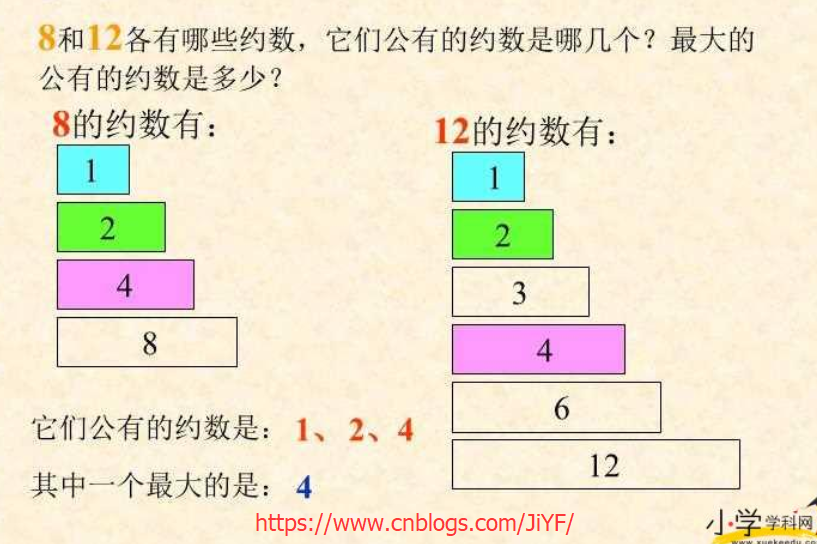
 2.2 最小公倍数和最大公约数关系

两个数的乘积等于这两个数的最大公约数与最小公倍数的乘积。

3.C#代码实现

代码：

    class Program
    {
        static void Main(string[] args)
        {
            int n = GetMinimumCommonMultiple(3, 5);
            System.Console.WriteLine("3,5最小公倍数为:" + n.ToString());
            n = GetMinimumCommonMultiple(2, 4);
            System.Console.WriteLine("2,4最小公倍数为:" + n.ToString());


            int numb = GetGreatestCommonDivisor(4, 8);
            System.Console.WriteLine("4,8最大公约数为:" + numb.ToString());
            numb = GetGreatestCommonDivisor(3, 15);
            System.Console.WriteLine("3,15最大公约数为:" + numb.ToString());



            System.Console.Read();
        }


        /// <summary>
        /// //最大公约数 
        /// </summary>
        static int GetGreatestCommonDivisor(int a, int b)
        {
            if (a < b)
            {
                a = a + b;
                b = a - b;
                a = a - b;
            }
            return (a % b == 0) ? b : GetGreatestCommonDivisor(a % b, b);
        }

        /// <summary>
        /// //最小公倍数 
        /// </summary>
        static int GetMinimumCommonMultiple(int a, int b)
        {
            return a * b / GetGreatestCommonDivisor(a, b);
        }
    }

4.程序测试