高数学习笔记之向量内积(点乘)和外积(叉乘)概念及几何意义

0x00 概述

在机器学习的过程中，需要了解向量内积（点乘）和外积（叉乘）概念及几何意义。

 

0x01 向量的内积（点乘）

1.1 定义

概括地说，向量的内积（点乘/数量积）。对两个向量执行点乘运算，就是对这两个向量对应位一一相乘之后求和的操作，如下所示，对于向量a和向量b：

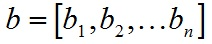
 a和b的点积公式为：

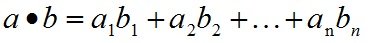
这里要求一维向量a和向量b的行列数相同。注意：点乘的结果是一个标量(数量而不是向量)

定义：两个向量a与b的内积为 a·b = |a||b|cos∠(a, b)，特别地，0·a =a·0 = 0；若a，b是非零向量，则a与b****正交的充要条件是a·b = 0。

 

1.2 向量内积的性质

'''
1. a^2 ≥ 0；当a^2 = 0时，必有a = 0. （正定性）
2. a·b = b·a. （对称性）
3. (λa + μb)·c = λa·c + μb·c，对任意实数λ, μ成立. （线性）
4. cos∠(a,b) =a·b/(|a||b|).
5. |a·b| ≤ |a||b|，等号只在a与b共线时成立.

'''

 

1.3 向量内积的几何意义

 内积（点乘）的几何意义包括：

'''
1. 表征或计算两个向量之间的夹角
2. b向量在a向量方向上的投影

'''

有公式：

 

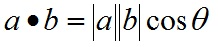
 推导过程如下，首先看一下向量组成：

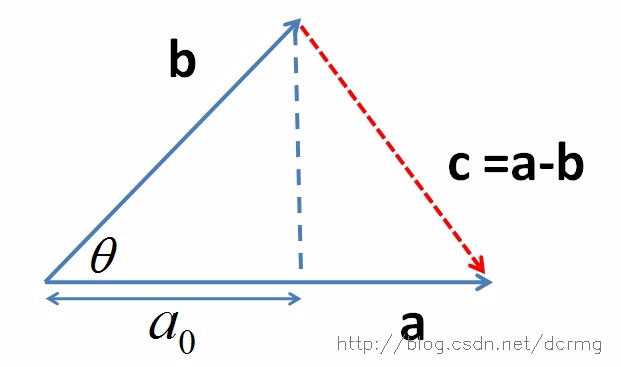
 定义向量c：

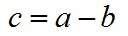
 根据三角形余弦定理（这里a、b、c均为向量，下同）有：

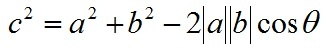
 根据关系c=a-b有：

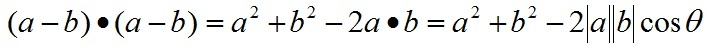
即：

a∙b=|a||b|cos⁡(θ)

向量a，b的长度都是可以计算的已知量，从而有a和b间的夹角θ：

θ=arccos⁡(a∙b|a||b|)

进而可以进一步判断两个向量是否同一方向或正交(即垂直)等方向关系，具体对应关系为：

'''
a∙b>0→方向基本相同，夹角在0°到90°之间
a∙b=0→ 正交，相互垂直
a∙b<0→ 方向基本相反，夹角在90°到180°之间

'''

 

0x02 向量的外积（叉乘）

2.1 定义

概括地说，两个向量的外积，又叫叉乘、叉积向量积，其运算结果是一个向量而不是一个标量。并且两个向量的外积与这两个向量组成的坐标平面垂直。

定义：向量a与b的外积a×b是一个向量，其长度等于|a×b| = |a||b|sin∠(a,b)，其方向正交于a与b。并且，(a,b,a×b)构成右手系。
特别地，0×a = a×0 = 0.此外，对任意向量a，a×a=0。

对于向量a和向量b：

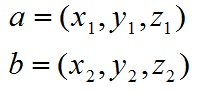
a和b的外积公式为：

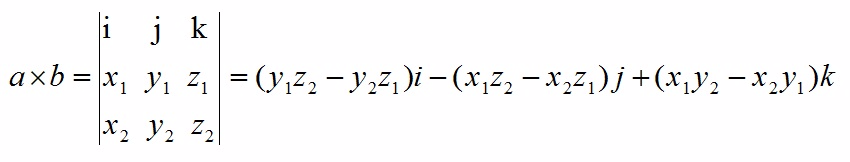
其中：

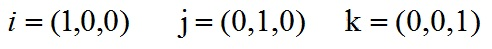
根据i、j、k间关系，有：

 

2.2 向量外积的性质

'''
1. a × b = -b × a. （反称性）
2. (λa + μb) × c = λ(a ×c) + μ(b ×c). （线性）

'''

 

2.3 向量外积的几何意义

在三维几何中，向量a和向量b的外积结果是一个向量，有个更通俗易懂的叫法是法向量，该向量垂直于a和b向量构成的平面。

在3D图像学中，外积的概念非常有用，可以通过两个向量的外积，生成第三个垂直于a，b的法向量，从而构建X、Y、Z坐标系。如下图所示：

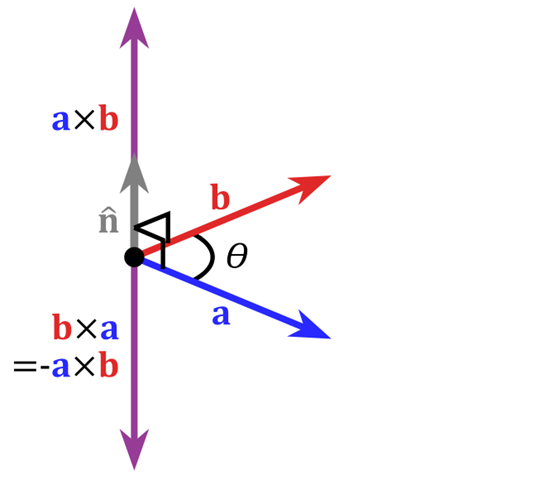
在二维空间中，外积还有另外一个几何意义就是：|a×b|在数值上等于由向量a和向量b构成的平行四边形的面积。