机器学习笔记之为什么逻辑回归的损失函数是交叉熵
0x00 概要
逻辑回归(logistic regression)在机器学习中是非常经典的分类方法,周志华教授的《机器学习》书中称其为对数几率回归,因为其属于对数线性模型。
在算法面试中,逻辑回归也经常被问到,常见的面试题包括:
- 逻辑回归推导;
- 逻辑回归如何实现多分类?
- SVM与LR的联系与区别?
- 逻辑回归反向传播伪代码;
大家可以思考下能不能回答/推导出,但这次讨论的问题是:
为什么逻辑回归损失函数是交叉熵?
初看这个问题感觉很奇怪,但是其中的知识包含了LR的推导与理解。在我个人看来,可以从两个角度看待这个问题:
''' 【1】从极大似然估计的角度可以推导出交叉熵;
【2】从KL散度(熵的角度)去理解; '''
0x01 极大似然估计
对于逻辑回归,我们一般通过极大似然估计来求解参数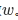
首先假设两个逻辑回归的两个条件概率:
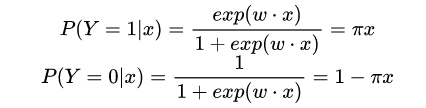
学习时,采用极大似然估计来估计模型的参数,似然函数为:
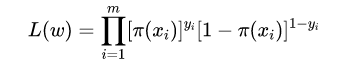
对数似然函数(采用对数似然函数是因为上述公式的连乘操作易造成下溢)为:
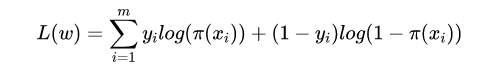
对其求最大值,估计参数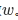 :
:
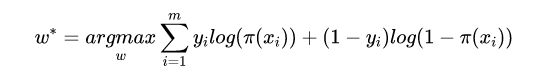
再将其改为最小化负的对对数似然函数:

如此,就得到了Logistic回归的损失函数,即机器学习中的「二元交叉熵」(Binary crossentropy):
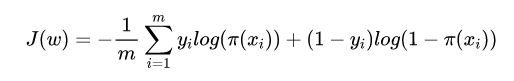
此时转变为以负对数似然函数为目标函数的最优化问题,采用梯度下降法进行优化。
0x02 KL散度
KL散度这个概念知道的人可能相对极大似然估计更少一点,具体可以看机器学习笔记---信息熵。
简单来说,「KL散度是衡量两个概率分布的差异」。
逻辑回归模型最后的计算结果(通过sigmoid或softmax函数)是各个分类的概率(可以看做是各个分类的概率分布)。那么假设真实的概率分布是,估计得到的概率分布是, 这两个概率分布的距离如何去衡量?在信息论中,「相对熵」,也就是KL散度可以衡量两个概率分布的差异性。具体公式为:
并且简单转化,可以得到:
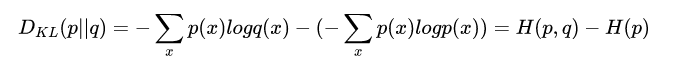

因为交叉熵越大,KL散度越大,也可以用交叉熵来衡量两个概率分布之间的距离,所以逻辑回归使用交叉熵作为逻辑回归的损失函数。
0x03 转载
https://mp.weixin.qq.com/s/LPfrzLCVBj3SUQAf9fnlmA
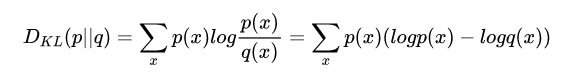

 浙公网安备 33010602011771号
浙公网安备 33010602011771号