高数笔记之期望和均值的区别

0x00 概述

期望和均值原来容易会弄混，但其实他们是完全不同的概念，那么分别来介绍均值和期望看看他们的不同点。

 

0x01 均值

均值，其实是针对实验观察到的特征样本而言的。比如我们实验结果得出了x1,x2,x3…..xn这n个值，那么我们的均值计算是

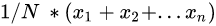
比如我们进行掷骰子，掷了六次，点数分别为2，2，2，4，4，4，这六次的观察就是我们的样本，于是我们可以说均值为(2+2+2+4+4+4)/6=3。

但是千万不能说期望是3，说概率是3就明显的弄混了均值和期望的概念，下面解释一下期望的概念。

 

0x02 期望

期望是针对于随机变量而言的一个量，可以理解是一种站在“上帝视角”的值。针对于他的样本空间而言的。

均值是一个统计量(对观察样本的统计)，期望是一种概率论概念，是一个数学特征。

首先给出定义公式

那么上面那个掷骰子例子对应的期望求法如下：

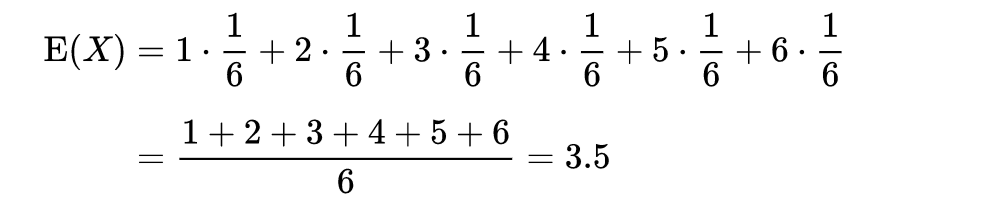
可以看出期望是与概率值联系在一起的，如果说概率是频率随样本趋于无穷的极限 ，期望就是平均数随样本趋于无穷的极限，可以看出均值和期望的联系也是大数定理联系起来的。

 

0x03 例子

上面说到期望就是平均数随样本趋于无穷的极限，那么这句话是什么意思呢？

'''
我们还是以上面的掷骰子为例子：

如果我们掷了无数次的骰子，然后将其中的点数进行相加，然后除以他们掷骰子的次数得到均值，这个有无数次样本得出的均值就趋向于期望。类似于下面这样：
'''

 

 

 

 

0x04 总结

概率是频率随样本趋于无穷的极限

期望是平均数随样本趋于无穷的极限

 

0x05 转载