机器学习笔记之sklearn的逻辑回归Logistics Regression实战
0x00 概述
本文介绍sklearn 逻辑回归模型的参数,以及具体的实战代码。
0x01 逻辑回归的二分类和多分类
上次介绍的逻辑回归的内容,基本都是基于二分类的。那么有没有办法让逻辑回归实现多分类呢?那肯定是有的,还不止一种。
实际上二元逻辑回归的模型和损失函数很容易推广到多元逻辑回归。比如总是认为某种类型为正值,其余为0值。
举个例子,要分类为A,B,C三类,那么就可以把A当作正向数据,B和C当作负向数据来处理,这样就可以用二分类的方法解决多分类的问题,这种方法就是最常用的one-vs-rest,简称OvR。而且这种方法也可以方便得推广到其他二分类模型中(当然其他算法可能有更好的多分类办法)。
另一种多元逻辑回归的方法是Many-vs-Many(MvM),它会选择一部分类别的样本和另一部分类别的样本来做逻辑回归二分类。
听起来很不可思议,但其实确实是能办到的。比如数据有A,B,C三个分类。
我们将A,B作为正向数据,C作为负向数据,训练出一个分模型。再将A,C作为正向数据,B作为负向数据,训练出一个分类模型。最后B,C作为正向数据,C作为负向数据,训练出一个模型。
通过这三个模型就能实现多分类,当然这里只是举个例子,实际使用中有其他更好的MVM方法。限于篇幅这里不展开了。
MVM中最常用的是One-Vs-One(OvO)。OvO是MvM的特例。即每次选择两类样本来做二元逻辑回归。
对比下两种多分类方法,通常情况下,Ovr比较简单,速度也比较快,但模型精度上没MvM那么高。MvM则正好相反,精度高,但速度上比不过Ovr。
0x02 逻辑回归的正则化
所谓正则化,其目的是为了减弱逻辑回归模型的精度,难道模型的准确度不是越高越好嘛?看看下面这张图就明白了:
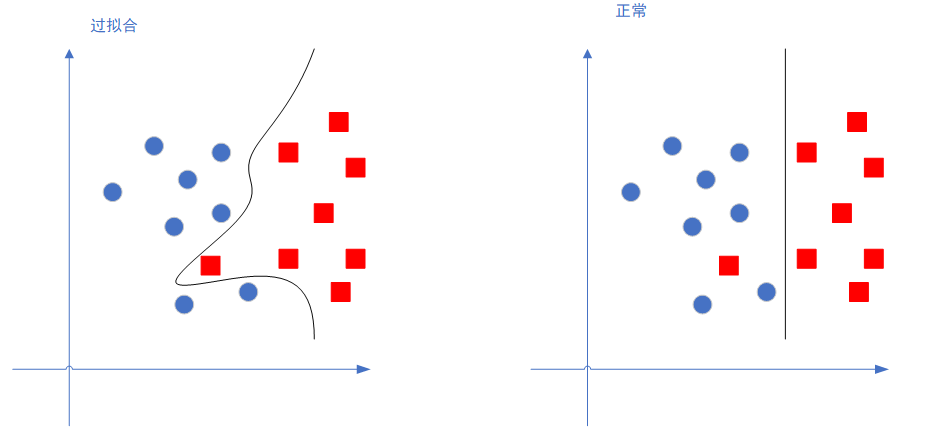
左边那个图就是过拟合的情况,过拟合其实就是模型的精度太过高了,它能非常好得匹配训练集的数据,但一旦有新的数据,就会表现得很差。
而我们要的非过拟合的模型是,精度可以差一些,但泛化性能,也就是对新的数据的识别能力,要比较好。
正则化就是减弱模型精度,提高泛化效果的这个东西。
0x03 sklearn各个参数
def LogisticRegression(penalty='l2', dual=False, tol=1e-4, C=1.0, fit_intercept=True, intercept_scaling=1, class_weight=None, random_state=None, solver='warn', max_iter=100, multi_class='warn', verbose=0, warm_start=False, n_jobs=None, l1_ratio=None ) 跟线性回归一比,逻辑回归的参数那还真是多啊,不过我们一个一个来看看参数都是什么意思吧。 - dual:对偶或者原始方法,布尔类型,默认为False。Dual只适用于正则化相为l2的‘liblinear’的情况,通常样本数大于特征数的情况下,默认为False。 - tol:停止迭代求解的阈值,单精度类型,默认为1e-4。 - C:正则化系数的倒数,必须为正的浮点数,默认为 1.0,这个值越小,说明正则化效果越强。换句话说,这个值越小,越训练的模型更泛化,但也更容易欠拟合。 - fit_intercept:是否要使用截距(在决策函数中使用截距),布尔类型,默认为True。 - intercept_scaling:官方解释比较模糊,我说下个人理解。浮点型,默认值是1.0。这个参数仅在“solver”参数(下面介绍)为“liblinear”“fit_intercept ”参数为True的时候生效。作用是给特征向量添加一个常量,这个常量就是intercept_scaling。比如原本的向量是[x],那么添加后就变成[x,intercept_scaling]。 - class_weight:分类权重,可以是一个dict(字典类型),也可以是一个字符串"balanced"字符串。默认是None,也就是不做任何处理,而"balanced"则会去自动计算权重,分类越多的类,权重越低,反之权重越高。也可以自己输出一个字典,比如一个 0/1 的二元分类,可以传入{0:0.1,1:0.9},这样 0 这个分类的权重是0.1,1这个分类的权重是0.9。这样的目的是因为有些分类问题,样本极端不平衡,比如网络攻击,大部分正常流量,小部分攻击流量,但攻击流量非常重要,需要有效识别,这时候就可以设置权重这个参数。 - random_state:设置随机数种子,可以是int类型和None,默认是None。当"solver"参数为"sag"和"liblinear"的时候生效。 - verbose:输出详细过程,int类型,默认为0(不输出)。当大于等于1时,输出训练的详细过程。仅当"solvers"参数设置为"liblinear"和"lbfgs"时有效。 - warm_start:设置热启动,布尔类型,默认为False。若设置为True,则以上一次fit的结果作为此次的初始化,如果"solver"参数为"liblinear"时无效。 - max_iter:最大迭代次数,int类型,默认-1(即无限制)。注意前面也有一个tol迭代限制,但这个max_iter的优先级是比它高的,也就如果限制了这个参数,那是不会去管tol这个参数的。
OK,上述就是对一些比较简略的参数的说明,但是还有几个重要的参数没讲到,这是因为这几个参数我觉得需要单独拎出来讲一讲。
sklearn逻辑回归参数 --penalty
正则化类型选择,字符串类型,可选'l1','l2','elasticnet'和None,默认是'l2',通常情况下,也是选择'l2'。这个参数的选择是会影响到参数'solver'的选择的,下面会介绍。
其中'l1'和'l2'。分别对应L1的正则化和L2的正则化,'elasticnet'则是弹性网络(这玩意我也不大懂),默认是L2的正则化。
在调参时如果主要的目的只是为了解决过拟合,一般penalty选择L2正则化就够了。但是如果选择L2正则化发现还是过拟合,即预测效果差的时候,就可以考虑L1正则化。另外,如果模型的特征非常多,我们希望一些不重要的特征系数归零,从而让模型系数稀疏化的话,也可以使用L1正则化。
penalty参数的选择会影响我们损失函数优化算法的选择。即参数solver的选择,如果是L2正则化,那么4种可选的算法{‘newton-cg’,‘lbfgs’,‘liblinear’,‘sag’}都可以选择。但是如果penalty是L1正则化的话,就只能选择‘liblinear’了。这是因为L1正则化的损失函数不是连续可导的,而{‘newton-cg’,‘lbfgs’,‘sag’}这三种优化算法时都需要损失函数的一阶或者二阶连续导数。而‘liblinear’并没有这个依赖。最后还有一个'elasticnet',这个只有solver参数为'saga'才能选。
sklearn逻辑回归参数 --solver
优化算法参数,字符串类型,一个有五种可选,分别是"newton-cg","lbfgs","liblinear","sag","saga。默认是"liblinear"。分别介绍下各个优化算法:
- a) liblinear:使用了开源的liblinear库实现,内部使用了坐标轴下降法来迭代优化损失函数。
- b) lbfgs:拟牛顿法的一种,利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。
- c) newton-cg:也是牛顿法家族的一种,利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。
- d) sag:即随机平均梯度下降,是梯度下降法的变种,和普通梯度下降法的区别是每次迭代仅仅用一部分的样本来计算梯度,适合于样本数据多的时候。
在优化参数的选择上,官方是这样建议的: - e)saga:优化的,无偏估计的sag方法。(‘sag’ uses a Stochastic Average Gradient descent, and ‘saga’ uses its improved, unbiased version named SAGA.)
对小的数据集,可以选择"liblinear",如果是大的数据集,比如说大于10W的数据,那么选择"sag"和"saga"会让训练速度更快。
对于多分类问题,只有newton-cg,sag,saga和lbfgs能够处理多项损失(也就是MvM的情况,还记得上面说到的多分类嘛?),而liblinear仅处理(OvR)的情况。啥意思,就是用liblinear的时候,如果是多分类问题,得先把一种类别作为一个类别,剩余的所有类别作为另外一个类别。一次类推,遍历所有类别,进行分类。
这个的选择和正则化的参数也有关系,前面说到"penalty"参数可以选择"l1","l2"和None。这里'liblinear'是可以选择'l1'正则和'l2'正则,但不能选择None,'newton-cg','lbfgs','sag'和'saga'这几种能选择'l2'或no penalty,而'saga'则能选怎'elasticnet'正则。好吧,这部分还是挺绕的。
归纳一下吧,二分类情况下,数据量小,一般默认的'liblinear'的行,数据量大,则使用'sag'。多分类的情况下,在数据量小的情况下,追求高精度,可以用'newton-cg'或'lbfgs'以'MvM'的方式求解。数据量一大还是使用'sag'。
当然实际情况下还是要调参多次才能确定参数,这里也只能给些模糊的建议。
sklearn逻辑回归参数 --multi_class
multi_class参数决定了我们分类方式的选择,有 ovr和multinomial两个值可以选择,默认是 ovr。
ovr即前面提到的one-vs-rest(OvR),而multinomial即前面提到的many-vs-many(MvM)。如果是二元逻辑回归,ovr和multinomial并没有任何区别,区别主要在多元逻辑回归上。
0x04 sklearn代码实例
import numpy as np import matplotlib.pyplot as plt from sklearn import linear_model, datasets # 加载鸢尾花数据 iris = datasets.load_iris() # 只采用样本数据的前两个feature,生成X和Y X = iris.data[:, :2] Y = iris.target h = .02 # 网格中的步长 # 新建模型,设置C参数为1e5,并进行训练 logreg = linear_model.LogisticRegression(C=1e5) logreg.fit(X, Y) # 绘制决策边界。为此我们将为网格 [x_min, x_max]x[y_min, y_max] 中的每个点分配一个颜色。 x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5 y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5 xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h)) Z = logreg.predict(np.c_[xx.ravel(), yy.ravel()]) # 将结果放入彩色图中 Z = Z.reshape(xx.shape) plt.figure(1, figsize=(4, 3)) plt.pcolormesh(xx, yy, Z, cmap=plt.cm.Paired) # 将训练点也同样放入彩色图中 plt.scatter(X[:, 0], X[:, 1], c=Y, edgecolors='k', cmap=plt.cm.Paired) plt.xlabel('Sepal length') plt.ylabel('Sepal width') plt.xlim(xx.min(), xx.max()) plt.ylim(yy.min(), yy.max()) plt.xticks(()) plt.yticks(()) plt.show()
运行上面那段代码会有如下的结果:
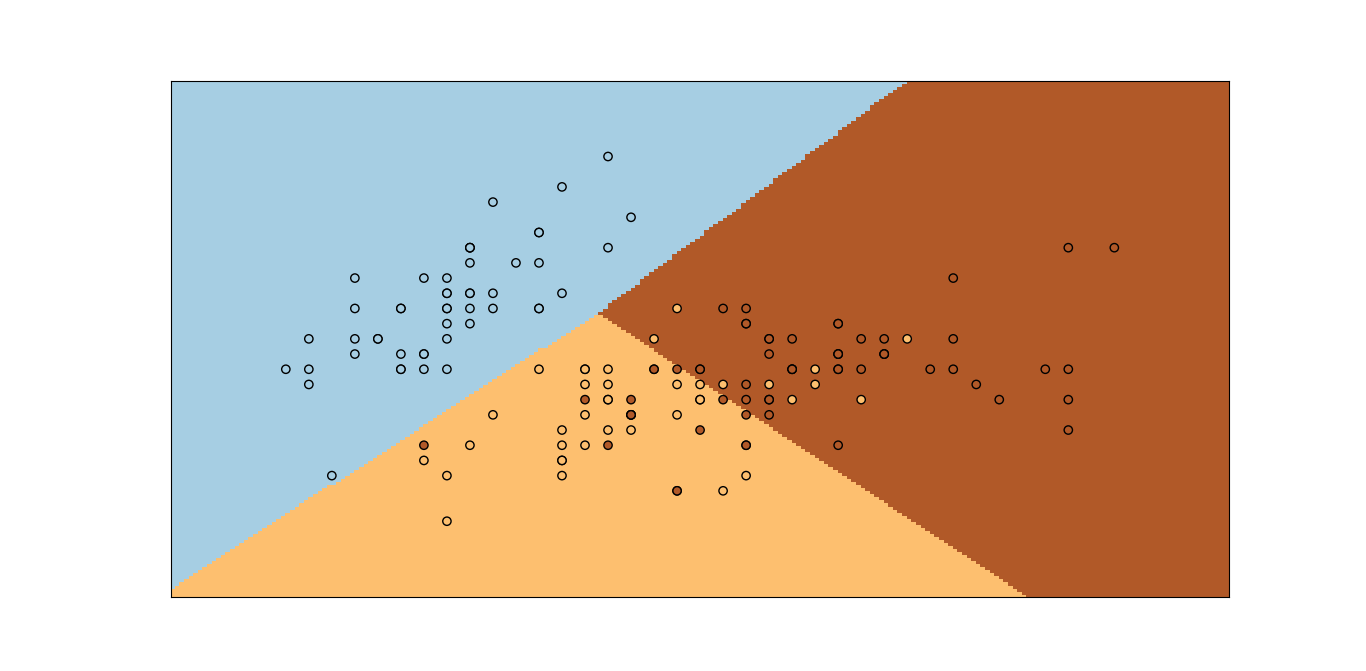
可以看到,已将三种类型的鸢尾花都分类出来了。
0x05 小结
逻辑回归算是比较简单的一种分类算法,而由于简单,所以也比较适合初学者初步接触机器学习算法。学习了之后,对后面一些更复杂的机器学习算法,诸如Svm,或更高级的神经网络也能有一个稍微感性的认知。
而实际上,Svm可以看作是逻辑回归的更高级的演化。而从神经网络的角度,逻辑回归甚至可以看作一个最初级,最浅层的神经网络。
逻辑回归就像是金庸小说里面,独孤九剑的第一式,最为简单,却又是其他威力极大的招式的基础,其他的招式都又第一式演化而出。
夯实基础,才能砥砺前行。
以上~

 浙公网安备 33010602011771号
浙公网安备 33010602011771号