深度学习笔记之用Python实现多层感知器神经网络
0x00 概述
强大的库已经存在了,如:TensorFlow,PyTorch,Keras等等。
本文将介绍在Python中创建多层感知器(MLP)神经网络的基本知识。
感知器是神经网络的基本组成部分。感知器的输入函数是权重,偏差和输入数据的线性组合。具体来说:
in_j = weight input + bias.(in_j =权重输入+偏差)
在每个感知器上,我们都可以指定一个激活函数g。
激活函数是一种确保感知器“发射”或仅在达到一定输入水平后才激活的数学方法。常见的非线性激活函数为S型,softmax,整流线性单位(ReLU)或简单的tanH。
激活函数有很多选项,但是在本文中我们仅涉及Sigmoid和softmax。
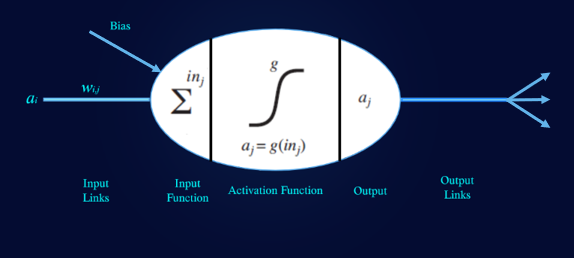
图1:感知器
对于有监督的学习,我们稍后将输入的数据通过一系列隐藏层转发到输出层。这称为前向传播。
在输出层,我们能够输出预测y。通过我们的预测y,我们可以计算误差| y*-y | 并使误差通过神经网络向后传播。这称为反向传播。
通过随机梯度下降(SGD)过程,将更新隐藏层中每个感知器的权重和偏差。
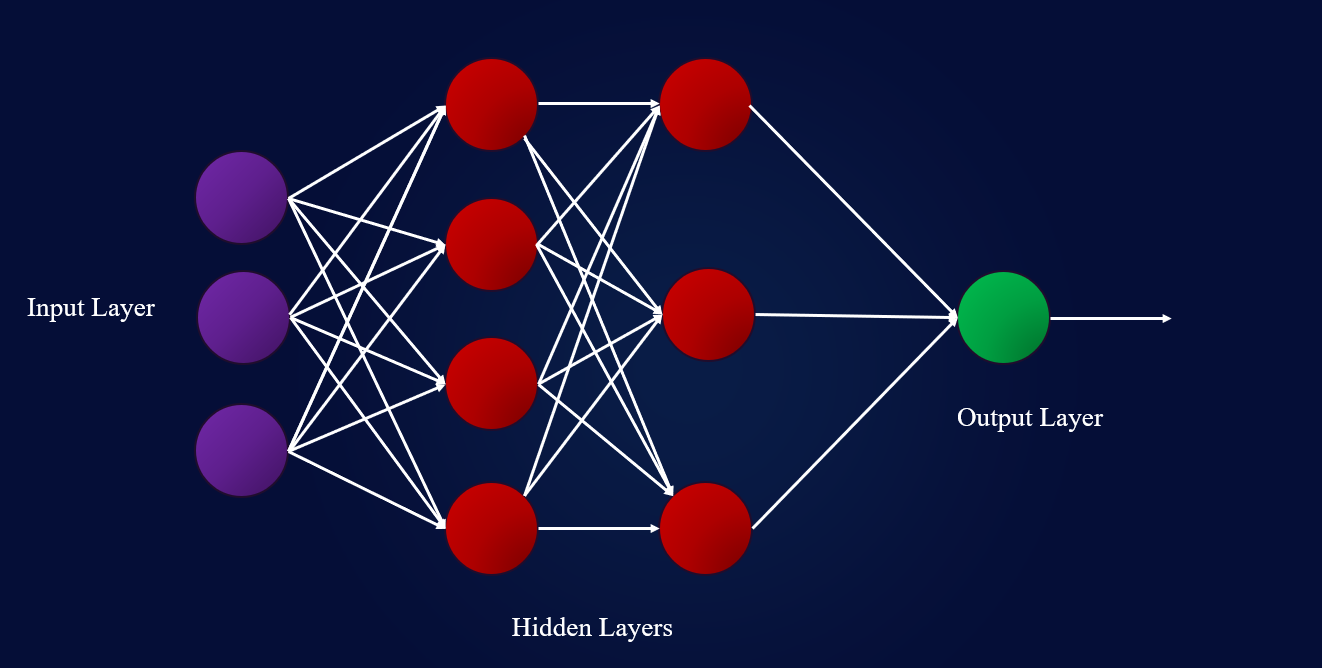
图2:神经网络的基本结构
现在我们已经介绍了基础知识,让我们实现一个神经网络。我们的神经网络的目标是对MNIST数据库中的手写数字进行分类。我将使用NumPy库进行基本矩阵计算。
在我们的问题中,MNIST数据由 [748,1] 矩阵中的8位颜色通道表示。从本质上讲,我们有一个 [748,1] 的数字矩阵,其始于[0,1,.... 255],其中0表示白色,255表示黑色。
结果
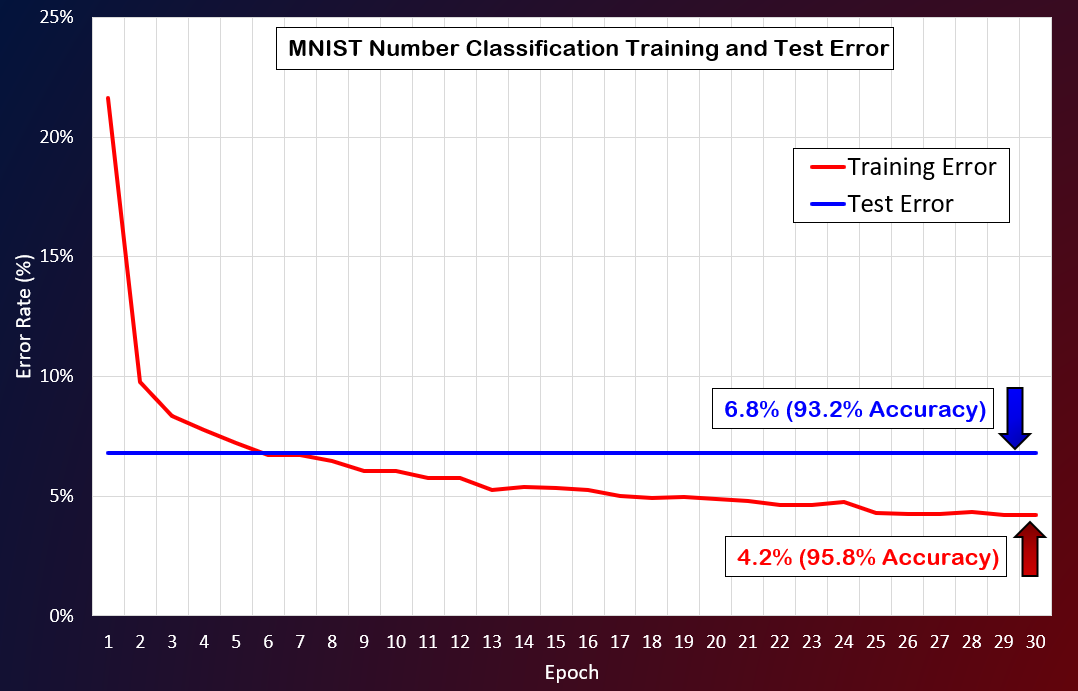
MNIST手写数字数据库包含60,000个用于训练目的的手写示例和10,000个用于测试目的的示例。在对60,000个示例进行了30个epoch的训练之后,我在测试数据集上运行了经过训练的神经网络,并达到了93.2%的准确性。甚至可以通过调整超参数来进一步优化。
本文分为5个部分。这些部分是:
- 激活函数
- 权重初始化
- 偏差初始化
- 训练算法
- 进行预测
0x01 激活函数
Sigmoid是由等式1 /(1+ exp(-x))定义的激活函数,将在隐藏层感知器中使用。
Softmax是一个激活函数,当我们要将输入分为几类时,它通常在输出层中使用。在我们的例子中,我们希望将一个数字分成10个bucket[0,1,2,…,9]中的一个。它计算矩阵中每个条目的概率;概率将总计为1。具有最大概率的条目将对应于其预测,即0,1,…,9。Softmax定义为exp(x)/ sum(exp(x))。
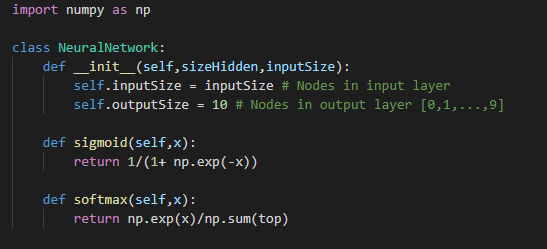
图3:激活函数的实现
0x02 权重初始化
对于我们的每个隐藏层,我们将需要初始化权重矩阵。有几种不同的方法可以做到这一点,这里是图4。
# 零初始化-初始化所有权重= 0
随机初始化-使用随机数初始化权重,而不是完全随机。我们通常使用标准正态分布(均值0和方差1)中的随机数。
Xavier初始化-使用具有设定方差的正态分布中的随机数初始化权重。我们将基于上一层的大小设置方差。
如上所述,进入感知器的边缘乘以权重矩阵。关键的一点是,矩阵的大小取决于当前图层的大小以及它之前的图层。明确地,权重矩阵的大小为[currentLayerSize,previousLayerSize]。
如上所述,进入感知器的边缘乘以权重矩阵。关键的一点是,矩阵的大小取决于当前图层的大小以及它之前的图层。明确地,权重矩阵的大小为[currentLayerSize,previousLayerSize]。
假设我们有一个包含100个节点的隐藏层。我们的输入层的大小为[748,1],而我们所需的输出层的大小为[10,1]。输入层和第一个隐藏层之间的权重矩阵的大小为[100,748]。隐藏层之间的每个权重矩阵的大小为[100,100]。最后,最终隐藏层和输出层之间的权重矩阵的大小为[10,100]。
出于教育目的,我们将坚持使用单个隐藏层;在最终模型中,我们将使用多层。
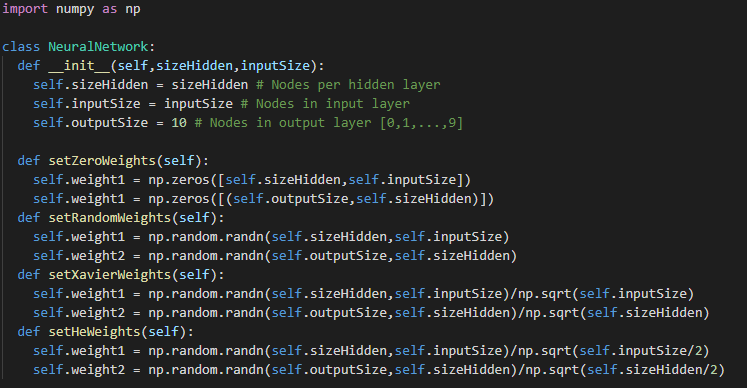
图4:权重初始化实现
0x03 偏差初始化
像权重初始化一样,偏置矩阵的大小取决于图层大小,尤其是当前图层大小。偏置初始化的一种方法是将偏置设置为零。
对于我们的实现,我们将需要为每个隐藏层和输出层提供一个偏差。偏置矩阵的大小为[100,1],基于每个隐藏层100个节点,而输出层的大小为[10,1]。

图5:偏置初始化实现
0x04 训练算法
前面已经说过,训练是基于随机梯度下降(SGD)的概念。在SGD中,我们一次只考虑一个训练点。
在我们的示例中,我们将在输出层使用softmax激活。将使用“交叉熵损失”公式来计算损失。对于SGD,我们将需要使用softmax来计算交叉熵损失的导数。也就是说,此导数减少为y -y,即预测y减去期望值y。

图6:关于softmax激活的交叉熵损失及其导数
我们还需要编写S型激活函数的导数。在图7中,定义了S型函数及其衍生函数
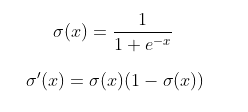
图7:Sigmoid函数(上)及其导数(下)
通常,神经网络将允许用户指定几个“超参数”。在我们的实施中,我们将着重于允许用户指定epoch,批处理大小,学习率和动量。还有其他优化技术:
- 学习率(LR):学习率是一个参数,用户可以通过它指定网络允许我们学习和更新其参数的速度。选择一个好的学习率是一门艺术。如果LR太高,我们可能永远不会收敛于良好的可接受的训练错误。如果LR太低,我们可能会浪费大量的计算时间。
- epoch:epoch是整个训练集中的一个迭代。为了确保我们不会过度拟合早期样本中的数据,我们会在每个时期之后对数据进行随机排序。
- 批次大小:通过Epoc2h的每次迭代,我们将分批训练数据。对于批次中的每个训练点,我们将收集梯度,并在批次完成后更新权重/偏差。
- 动量:这是一个参数,我们将通过收集过去的梯度的移动平均值并允许在该方向上的运动来加速学习。在大多数情况下,这将导致更快的收敛。典型值范围从0.5到0.9。
下面,是一些通用的伪代码来模拟反向传播学习算法的概况。
为了便于阅读,已将诸如计算输出和将训练数据分成批次之类的任务作为注释编写。

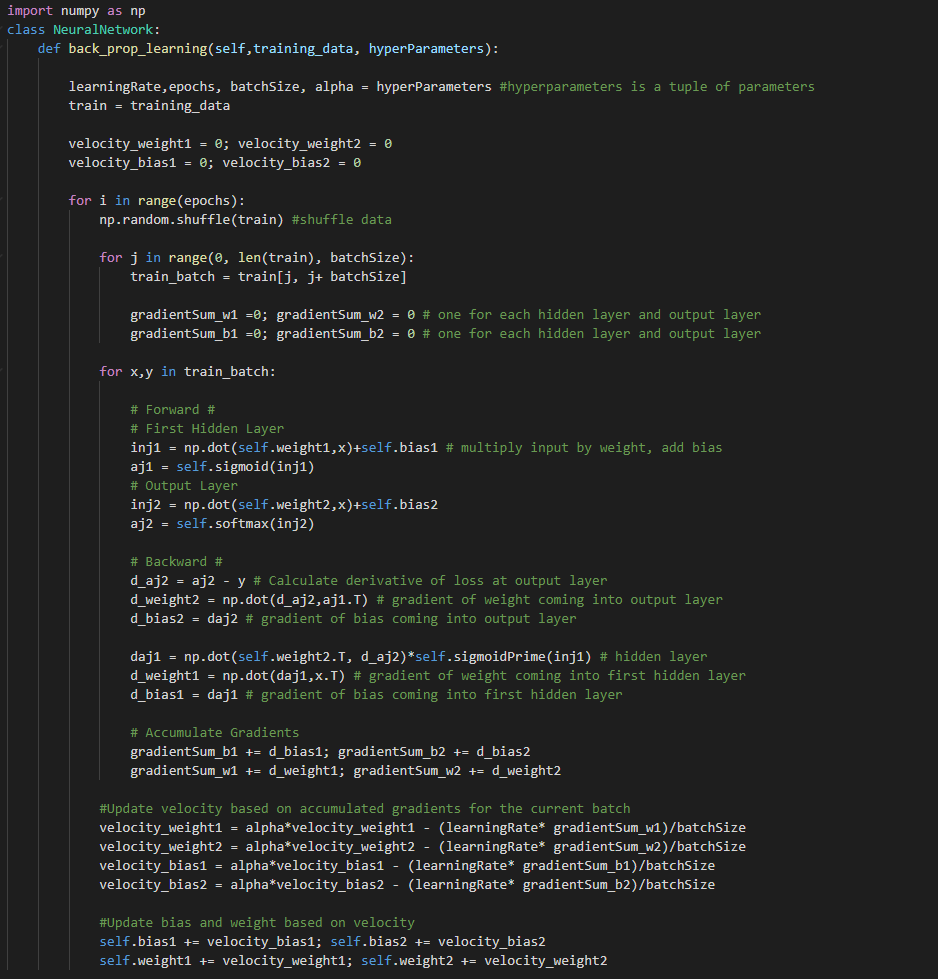
0x05 做出预测
现在,我们仅缺少此实现的一个关键方面。预测算法。在编写反向传播算法的过程中,我们已经完成了大部分工作。我们只需要使用相同的前向传播代码即可进行预测。输出层的softmax激活函数将计算大小为[10,1]的矩阵中每个条目的概率。
我们的目标是将数字分类为0到9。因此,aj2矩阵的索引将与预测相对应。概率最大的索引将由np.argmax()选择,并将作为我们的预测。

0x06 结论
我们已经用Python编写了神经网络的实现。
但是,我们如何选择最佳参数?我们可以使用算法的一般知识来选择有意义的超参数。
我们需要选择能概括但不能过度拟合数据的超参数。我们可以调整动量,学习率,时期数,批处理大小和隐藏节点的数量,以实现我们的目标。向前迈出一步,我们可以编写更多算法来为我们做这件事!
遗传算法是一种AI算法,可用于选择最佳参数。遗传算法的思想是创建一组具有不同参数的子代,并让他们产生与参数相关的测试错误。我们可以对具有最佳超参数的神经网络进行繁殖和变异,以找到性能更好的参数。花费大量时间后,我们将能够学习有关超参数情况的大量知识,并找到新的最佳超参数值。
我们还可以采取其他措施来减少测试错误吗?是的,我们可以缩放输入数据。像许多算法一样,数量更多会对算法的结果产生重大影响。在我们的示例中,数字范围为[0到255]。如果我们按比例缩放数字,使它们的范围从[0到1],则可以减少该偏差。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号