ROC曲线与AUC
基础介绍
ROC全称是“受试者工作特征”(Receiver Operating Characteristic)。ROC曲线下的面积就是AUC(Area Under the Curve)。AUC用于衡量“二分类问题”机器学习算法的性能。介绍定义前,首先需要知道基础相关概念:
1)分类阈值,即设置判断样本为正例的阈值thr,例如针对预测概率 P(y=1 | x) >= thr (常取thr=0.5) 或 预测分数 score >= thr (常取thr=0)则判定样本为正例
2)混淆矩阵

真正例率 TPR (True Positive Rate):所有正例中,有多少被正确地判定为正。
假正例率 FPR (False Positive Rate):所有负例中,有多少被错误地判定为正。
其实 TPR 就是 查全率/召回率(recall)。 阈值取不同值,TPR和FPR的计算结果也不同,最理想情况下,我们希望所有正例 & 负例 都被成功预测 TPR=1,FPR=0,即 所有的正例预测值 > 所有的负例预测值,此时阈值取最小正例预测值与最大负例预测值之间的值即可。
TPR越大越好,FPR越小越好,但这两个指标通常是矛盾的。为了增大TPR,可以预测更多的样本为正例,与此同时也增加了更多负例被误判为正例的情况。
ROC曲线
给定m+个正例和m−个反例,根据学习其预测结果对样例 从大到小 进行排序,然后把分类阈值设为最大,即把所有的样例均预测为反例,此时真正例率和假正例率都为0,得到标记点(FPR,TPR) = (0,0)。然后逐渐增大阈值,即依次将每个样例划分为正例。设前一个标记点坐标为(x,y),则
若当前为真正例,则对应标记点的坐标为(x, y + 1/m+); 若当前为假正例,则对应标记点的坐标为(x + 1/m-, y);
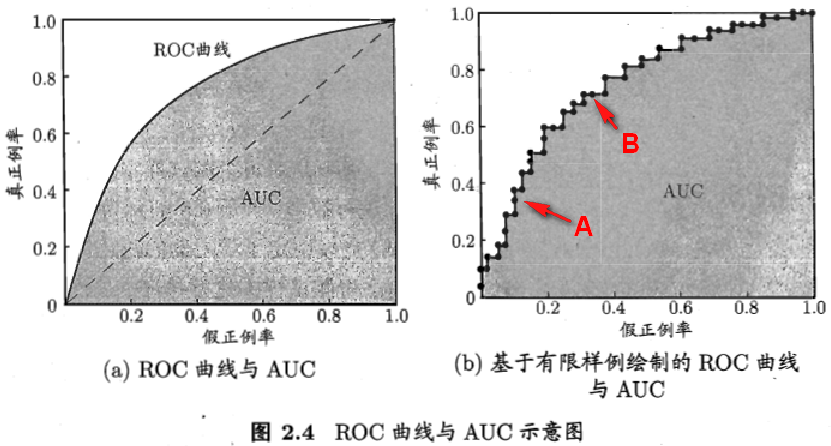
最后一个阈值会将所有样本预测为正例,则得到标记点 (FPR,TPR) = (1,1)。将这样依次到的一系列 (FPR, TPR) 作图于二维坐标系中得到的曲线,就是ROC曲线,因此,ROC曲线是一个单调曲线,而且肯定经过点(0,0)与(1,1)。如下左图摘自西瓜书中的AUC曲线图示例。基于有限样本作ROC图(b)时,可以看到曲线每次都是一个“爬坡”,遇到正例往上爬一格(1/m+),错了往右爬一格(1/m-),显然往上爬对于算法性能来说是最好的。
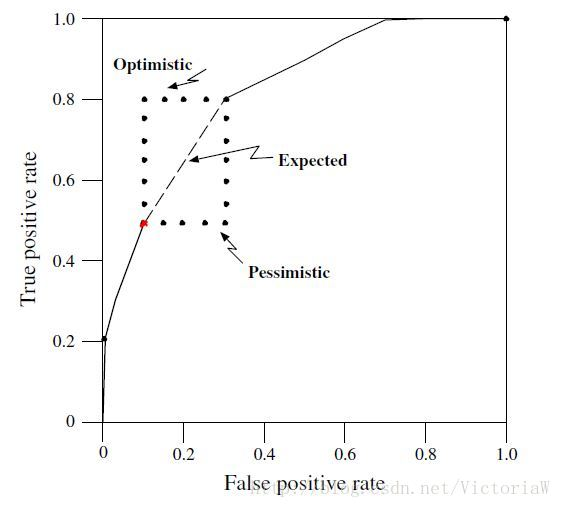
若分类器打分结果中,多个正负样本得分是一样,比如有10个实例得分相同,其中6个正例,4个负例,此时我们可以画“期望”曲线,如下右图所示。
ROC曲线分析
上图(a)虚线表示随机猜测算法的ROC曲线。
ROC曲线距离左上角越近,证明分类器效果越好。如果一条算法1的ROC曲线完全包含算法2,则可以断定性能算法1>算法2。这很好理解,此时任做一条 横线(纵线),任意相同TPR(FPR) 时,算法1的FPR更低(TPR更高),故显然更优。
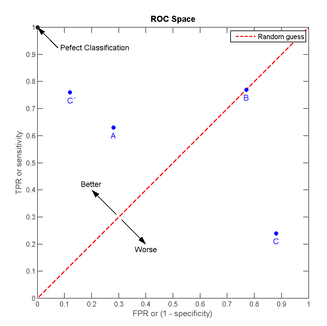
从上面ROC图中的几个标记点,我们可以做一些直观分析:
我们可以看出,左上角的点(TPR=1,FPR=0),为完美分类,也就是这个医生医术高明,诊断全对。点A(TPR>FPR),说明医生A的判断大体是正确的。中线上的点B(TPR=FPR),也就是医生B全都是蒙的,蒙对一半,蒙错一半;下半平面的点C(TPR<FPR),这个医生说你有病,那么你很可能没有病,医生C的话我们要反着听,为真庸医。
很多时候两个分类器的ROC曲线交叉,无法判断哪个分类器性能更好,这时可以计算曲线下的面积AUC,作为性能度量。
AUC的计算
ROC曲线下方由梯形组成,矩形可以看成特征的梯形。因此,AUC的面积可以这样算:(上底+下底)* 高 / 2,曲线下面的面积可以由多个梯形面积叠加得到。AUC越大,分类器分类效果越好。

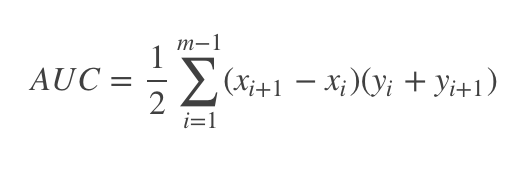
AUC = 1,是完美分类器,采用这个预测模型时,不管设定什么阈值都能得出完美预测。绝大多数预测的场合,不存在完美分类器。
0.5 < AUC < 1,优于随机猜测。这个分类器(模型)妥善设定阈值的话,能有预测价值。
AUC = 0.5,跟随机猜测一样,模型没有预测价值。
AUC < 0.5,比随机猜测还差;但只要总是反预测而行,就优于随机猜测。
Rank损失与AUC的关系
西瓜书中关于 Rank Loss 的定义如下,式子计算的是:对所有正例,得分比其高的反例数之和,对于得分和该正例相同的反例数量除以2,然后归一化。
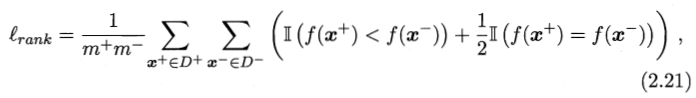
ROC曲线中,每遇到一个正例向上走一步,每遇到一个反例向右走一步。对于所有的正例,其横坐标所代表的步数就是得分比其高的反例数。为了便于理解,我们修改ROC空间的坐标,对横坐标乘以m-,对纵坐标乘以m+,在这个空间中每一步的刻度为1。
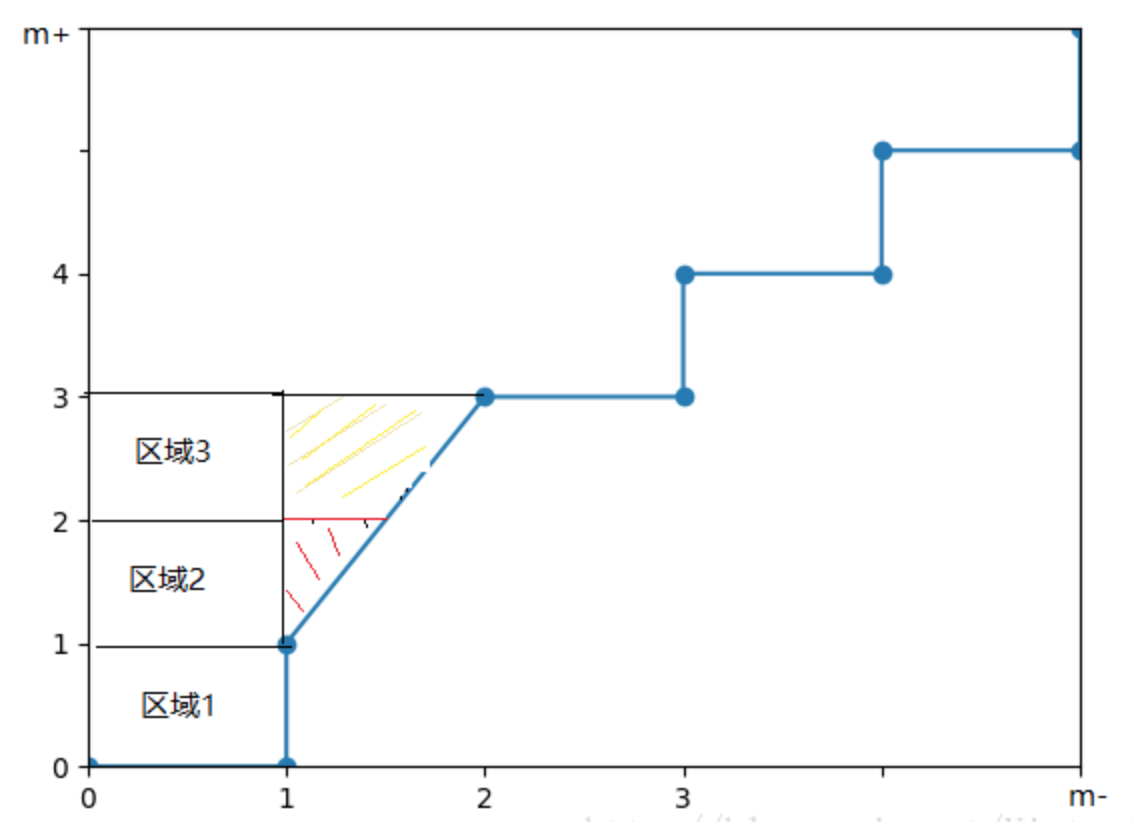
比如,上图中我们可以知道正反例顺序:【反,正,[正,正,反],反,正,反,正,反,正】。其中,[] 括起来的实例分数相同。
第1个正例,对应的区域1,区域1的面积为1*1=1,表示排在其前面的反例数为1。
第2个正例和第3个正例是特殊情况,它们和第2个反例得分是相同的。我们把这种情况一般化,假设有p个正例和q个反例的得分相同,那么有斜线对应的三角形的面积为q/2∗p,再加上第1个反例在第2、3个正例前面,所以再加上区域1和区域2的面积,整体就是期望斜线与纵轴围成的面积。这和上面说的AUC计算公式的思路其实是一样的。
所以可以得到如下等式,即 Lrank = 1 - AUC
![]()
AUC的物理意义
假设分类器的输出是样本属于正类的prob/socre,则 AUC的物理意义为,任取一对正负样本,正样本的预测值大于负样本的预测值的概率。
AUC物理意义的推导,可以结合AUC与Rank Loss的关系来理解。Rank Loss代表的物理意义其实是:任取一对正负样本,负样本的预测值大于正样本的预测值的概率。例如,假设这时按预测值排序样本为 【正 负 正正 负负负 正 负负】,那么“任取一对正负样本,负样本预测值大于正样本预测值的概率P” 可以表示为:
上面的式子可以直接等价转化为 Lrank 的形式,易知 AUC = 1 - Lrank 对应的物理意义即如上所述。
思考问题
1、在类不平衡的情况下,如正例90个,负例10个,直接把所有样本分类为正,准确率达到了90%,看似准确率很高,但这显然没有意义,这种全猜正算法的ROC曲线是如何的?
思考:
全猜正算法直接预测所有样本为正,即使预测所有正例=1,所有负例=1,那图上明确的标记点其实只有(0,0)和(1,1)两个起始点,按照上面说的相同分数取期望曲线,横轴 和 纵轴上点其实会分别均匀地从0以 1/m- 和 1/m+ 排列到1,此时期望ROC曲线和随机猜测是一样的,这样就避免了给这个傻乎乎的方法过高的正向指标。所以AUC可以处理这种类别不平衡问题的性能指标。
2、为什么ctr预估这类问题普遍使用AUC作为指标
思考:
ctr预估问题中并不会设置一个明确的阈值来得到强label(即转化为1/0),预测分数会作为随后给用户推荐的item的重要排序依据,而AUC更加注重算法性能在排序上的质量。此外,ROC曲线还有一些其他的优点:1)对问题的类别分布差异不敏感,比较鲁棒(参见ROC曲线 vs Precision-Recall曲线);2)AUC的计算比较方便(参见上面AUC计算公式)。
但是,理论上来讲,当学习问题是一个负例数量远大于正例数量的类别不平衡问题时,PRC曲线相比于ROC曲线更能真实地反映分类器的性能,为什么业界大都选择ROC曲线而不是PRC曲线作为ctr预估的线下指标,可以参看下一篇“ROC曲线 vs Precision-Recall曲线”。
参考资料
[1] 西瓜书
[2] 知乎专栏,提到了ROC与PRC的关系 https://zhuanlan.zhihu.com/p/28482121
[3] 介绍得相对比较全面 https://blog.csdn.net/qq_37059483/article/details/78595695
[4] https://community.alteryx.com/t5/Data-Science-Blog/ROC-Curves-in-Python-and-R/ba-p/138430



 浙公网安备 33010602011771号
浙公网安备 33010602011771号