求点集中的最近点对有以下两种方法:
设p1=(x1, y1), p2=(x2, y2), …, pn=(xn, yn)是平面上n个点构成的集合S,设计算法找出集合S中距离最近的点对。
解体思路
1、蛮力法(适用于点的数目比较小的情况下)
1)算法描述:已知集合S中有n个点,一共可以组成n(n-1)/2对点对,蛮力法就是对这n(n-1)/2对点对逐对进行距离计算,通过循环求得点集中的最近点对:
2)代码描述:
double MinDistance = double.maxvalue; //设置一个MinDistance存储最近点对的距离,初始值为无穷大
int PointIndex1,PointIndex2; //设置PointIndex1,PointIndex2分别存储最近点对的两个点编号
for (i=1; i< n; i++) //循环计算n(n-1)/2对点对的距离
{
for (j=i+1; j<=n; j++)
{
double PointDistance = Distance(S[i],S[j]); //求得point i和point j之间的距离
if PointDistance < MinDistance; //如果当前点对距离小于最小点对距离,则设置最小点对距离等于当前点对距离
{
MinDistance = PointDistance;
PointIndex1 = i;
PointIndex2 = j;
}
}
}
}
3)算法时间复杂度:算法一共要执行 n(n-1)/2次循环,因此算法复杂度为O(n2)
2、分治法
1)算法描述:已知集合S中有n个点,分治法的思想就是将S进行拆分,分为2部分求最近点对。算法每次选择一条垂线L,将S拆分左右两部分为SL和SR,L一般取点集S中所有点的中间点的x坐标来划分,这样可以保证SL和SR中的点数目各为n/2,
(否则以其他方式划分S,有可能导致SL和SR中点数目一个为1,一个为n-1,不利于算法效率,要尽量保持树的平衡性)
依次找出这两部分中的最小点对距离:δL和δR,记SL和SR中最小点对距离δ= min(δL,δR),如图1:
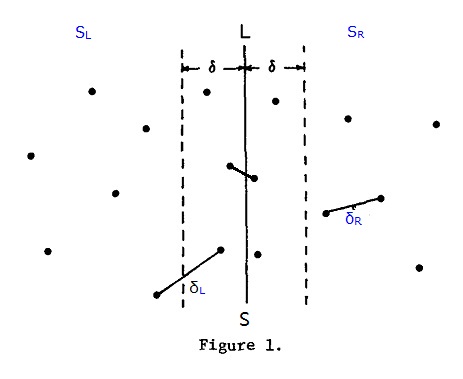
以L为中心,δ为半径划分一个长带,最小点对还有可能存在于SL和SR的交界处,如下图2左图中的虚线带,p点和q点分别位于SL和SR的虚线范围内,在这个范围内,p点和q点之间的距离才会小于δ,最小点对计算才有意义。
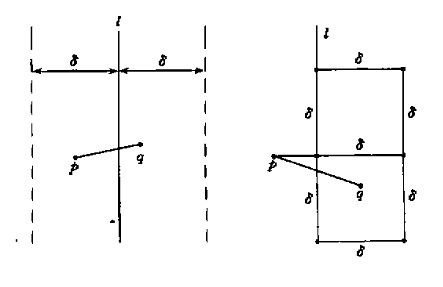
对于SL虚框范围内的p点,在SR虚框中与p点距离小于δ的顶多只有六个点,就是图二右图中的2个正方形的6的顶点。这个可以反推证明,如果右边这2个正方形内有7个点与p点距离小于δ,例如q点,则q点与下面正方形的四个顶点距离小于δ,则和δ为SL和SR中的最小点对距离相矛盾。因此对于SL虚框中的p点,不需求出p点和右边虚线框内所有点距离,只需计算SR中与p点y坐标距离最近的6个点,就可以求出最近点对,节省了比较次数。
(否则的话,最坏情形下,在SR虚框中有可能会有n/2个点,对于SL虚框中的p点,每次要比较n/2次,浪费了算法的效率)
代码描述:
1)对点集S的点x坐标进行升序排序,获得点集point[] array
2)令δ=∞; //δ为最大点位距离
3)Divide_conquer(point[] array,left,right) //分治法
if (left == right) then δ=∞; //如果point[]中只有一个点,则δ=∞
return δ;
else if (right - left ==1) // point[]中只有2个点,则直接求这两个点的距离
δ=d(Sx.[0],)Sx.[1]);
return δ;
else //如果point[]中多于2个点,则将point[]分治,以中心点画线,将point[]分为左右两部分A和B,
mid = (LeftIndex + rightIndex)>>1; //mid为当前段中的中间点index
double d1 = Closest_Pair(leftIndex,mid);
double d2 = Closest_Pair(mid +1,rightIndex);
d =min(d1,d2);
list<point> leftList = new <point>();
list<point> lrightList = new <point>();
// 分离出宽度为d,距point[mid]<=d的区间,其实也就是化了两条平行于x= point[mid].x的竖线。(之后还需要根据左边A的p,在右边选距离p.y<=d,在化两条横线,这样一个动态的矩形也就化出来了。(矩形包含两个正方形,一条边重合,也就是最多存在6(顶)点(鸽巢原理),可能满足条件 (如上面的图figure2)
循环遍历 数组
1. if (fabs(point[mid].x -point[i].x) <=d && i <= mid)
leftList.add(point[i] //左边符合条件的点
2. if (fabs(point[mid].x -point[i].x) <=d && i > mid)
rightList.add(point[i]) //右边符合条件的点
// 线性扫描
foreach ( point leftPoint in leftList)
{
foreach(point rightPoint in rightList)
d3=dis(leftPoint, rihgtPoint); //求左边点和右边点的最小值
if (d >d3)
{
d =d3; //更新最小值
}
}
return d;
详细的代码如下:
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace ConsoleApplication4
{
public class Point
{
public Point(double a, double b)
{
X = a;
Y = b;
}
double x;
public double X
{
get { return x; }
set { x = value; }
}
double y;
public double Y
{
get { return y; }
set { y = value; }
}
public static void Copy (Point a, Point b)
{
a.X = b.X;
a.Y = b.Y;
}
bool CompyX(Point a, Point b)
{
if (a.X != b.X)
{
return a.x < a.y;
}
return a.y < b.y;
}
public static double Dis(Point a, Point b)
{
return Math.Sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}
}
public static class SortHelper
{
public static void MergeSortByx(Point[] array)
{
int increaseMent = 1;
while (increaseMent < array.Length)
{
MergeByx(array, increaseMent);
increaseMent <<= 1;
}
}
public static void MergeByx(Point[] array, int increaseMent)
{
Point[] tempArray = new Point[array.Length];
for (int t = 0; t < tempArray.Length; t++)
{
tempArray[t] = new Point(0, 0); // 初始化
}
int lastIndex = array.Length - 1;
int l1 = 0; //第1个有序表的起始位置
int h1 = 0; //第1个有序表的结束位置
int l2 = 0; //第2个有序表的起始位置
int h2 = 0; //第2个有序表的结束位置
int m = 0; //临时表的初始位置
// 注意这里的临界条件(l2要存在,L2的index是: l1 + increaseMent<=lastIndex)
while (l1 + increaseMent <= lastIndex)
{
l2 = l1 + increaseMent;
h1 = l2 - 1;
h2 = l2 + increaseMent - 1 < lastIndex ? l2 + increaseMent - 1 : lastIndex;
int i = l1;
int j = l2;
//两个有序表中的记录没有排序完
while (i <= h1 && j <= h2)
{
//第1个有序表记录的关键码小于第2个有序表记录的关键码
if (array[i].X < array[j].X)
{
Point.Copy(tempArray[m], array[i]);
m++;
i++;
}
else //第2个有序表记录的关键码小于第1个有序表记录的关键码
{
Point.Copy(tempArray[m], array[j]);
m++;
j++;
}
}
//第1个有序表中还有记录没有排序完
while (i <= h1)
{
Point.Copy(tempArray[m], array[i]);
m++;
i++;
}
//第2个有序表中还有记录没有排序完
while (j <= h2)
{
Point.Copy(tempArray[m], array[j]);
m++;
j++;
}
l1 = h2 + 1;
}
//原顺序表中还有记录没有排序完
while (l1 <= lastIndex)
{
Point.Copy(tempArray[m], array[l1]);
m++;
l1++;
}
//临时顺序表中的记录复制到原顺序表,使原顺序表中的记录有序
for (int i = 0; i < array.Length; i++)
{
Point.Copy(tempArray[i], array[i]);
m++;
i++;
}
}
}
public class CalculateHelper
{
public double GetClosetDistant(Point[] array)
{
return GetClosetDistant(array, 0, array.Length - 1);
}
public double GetClosetDistant(Point[] array, int leftIndex, int rightIndex)
{
double distant = double.MaxValue;
//情况一: 当前区域只有一个点时,返回最大值,即当前值无效 (出口一)
if (leftIndex == rightIndex)
{
return distant;
}
// 情况二:当前区域只有两个点时,直接返回这两个点的距离 (出口二)
if (leftIndex + 1 == rightIndex)
{
return Point.Dis(array[leftIndex], array[rightIndex]);
}
// 按照x排序
SortHelper.MergeSortByx(array);
// 情况三,当前区域点的个数大于2的时候,需要采用分治法,把当前区域分成左右两个部分,直到满足情况一或二
int midIndex = (leftIndex + rightIndex) >> 1;
double leftDistance = GetClosetDistant(array, leftIndex, midIndex);
double rightDistance = GetClosetDistant(array, midIndex + 1, rightIndex);
distant = Math.Min(leftDistance, rightDistance); //求出左右两边区域的最小距离
if (distant < 0.43)
{
distant = distant;
}
for (int i = leftIndex; i <= midIndex; i++) //遍历左边的点
{
if (Math.Abs(array[i].X- array[midIndex].X) <distant) //选出左边区域距离x = array[midIndex].x <d的点 (画左边的1条竖线)
{
for (int j = midIndex + 1; j <= rightIndex; j++) //遍历右边的点
{
if (Math.Abs(array[i].X - array[midIndex].X) < distant) //选出左边区域距离x = array[midIndex].x <d的点 (画右边的1条竖线)
if (Math.Abs(array[i].Y - array[midIndex].Y) < distant) // 画出两条平行于 y= array[midIndex].Y的两条横线,到这一步时,
//矩形区域已经画好了,符合条件的点最多有6个
{
double bothDistance = Point.Dis(array[i], array[j]); //计算左右点的距离
if (bothDistance < distant)
{
distant = bothDistance; // 更新最小距离
}
if (distant < 0.43)
{
distant = distant;
}
}
}
}
}
if (distant < 0.43)
{
distant = distant;
}
return distant;
}
}
}
// 主函数
static void Main(string[] args)
{
CalculateHelper helper = new CalculateHelper();
Point[] array = new Point[14];
array[0] = new Point(2, 2);
array[1] = new Point(0.5, 0.5);
array[2] = new Point(0.25, 1);
array[3] = new Point(1, 2);
array[4] = new Point(3, 1);
array[5] = new Point(2, 0.7);
array[6] = new Point(1, 1);
array[7] = new Point(0.6, 0.8);
array[8] = new Point(0.9, 0.5);
array[9] = new Point(2, 1);
array[10] = new Point(4, 2);
array[11] = new Point(1.1, 0.5);
array[12] = new Point(8, 0.5);
array[13] = new Point(0.7, 2);
double dintance = helper.GetClosetDistant(array);
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号