分而治之方法与软件设计的模块化方法非常相似。为了解决一个大的问题,可以:
1) 把它分成两个或多个更小的问题;
2) 分别解决每个小问题;
3) 把各小问题的解答组合起来,即可得到原问题的解答。小问题通常与原问题相似,可以递归地使用分而治之策略来解决
1.[金块问题]
有一个老板有一袋金块。每个月将有两名雇员会因其优异的表现分别被奖励一个金块。按规矩,排名第一的雇员将得到袋中最重的金块,排名第二的雇员将得到袋中最轻的金块。根据这种方式,除非有新的金块加入袋中,否则第一名雇员所得到的金块总是比第二名雇员所得到的金块重。如果有新的金块周期性的加入袋中,则每个月都必须找出最轻和最重的金块。假设有一台比较重量的仪器,我们希望用最少的比较次数找出最轻和最重的金块。
其实这个问题和编程之美中的2.10是同一类型的。
2.棋盘覆盖问题
在一个2k x 2k ( 即:2^k x 2^k )个方格组成的棋盘中,恰有一个方格与其他方格不同,称该方格为一特殊方格,且称该棋盘为一特殊棋盘。在棋盘覆盖问题中,要用图示的4种不同形态的L型骨牌覆盖给定的特殊棋盘上除特殊方格以外的所有方格,且任何2个L型骨牌不得重叠覆盖。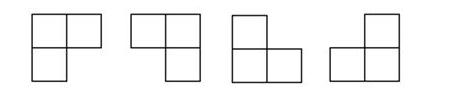
这里我们用分治法解决该问题。分治法是把一个规模很大的问题分解为多个规模较小、类似的子问题,然后递归地解决所有子问题,最后再由子问题的解决得到原问题的解决。
【解题思路】:将2^k x 2^k的棋盘,先分成相等的四块子棋盘,其中特殊方格位于四个中的一个,构造剩下没特殊方格三个子棋盘,将他们中的也假一个方格设为特殊方格。如果是:
左上的子棋盘(若不存在特殊方格)----则将该子棋盘右下角的那个方格假设为特殊方格
右上的子棋盘(若不存在特殊方格)----则将该子棋盘左下角的那个方格假设为特殊方格
左下的子棋盘(若不存在特殊方格)----则将该子棋盘右上角的那个方格假设为特殊方格
右下的子棋盘(若不存在特殊方格)----则将该子棋盘左上角的那个方格假设为特殊方格
当然上面四种,只可能且必定只有三个成立,那三个假设的特殊方格刚好构成一个L型骨架,我们可以给它们作上相同的标记。这样四个子棋盘就分别都和原来的大棋盘类似,我们就可以用递归算法解决。
// 残缺棋盘问题 public static void TileBoard(int[][] board, int tr, int tc, int dr, int dc, int size, ref int number) { if (size == 1) { return; } int t = number++; // 骨盘号自增 int s = (size >>1); // 分割棋盘 // 覆盖四分之一左上限子棋盘 if (dr < tr + s && dc < tc + s) { TileBoard(board, tr, tc, dr, dc, s, ref number); } else { board[tr+s -1][tc+s -1] =t; // 覆盖右下角 TileBoard(board, tr, tc, tr + s - 1, tc + s - 1, s, ref number); } // 覆盖四分之一右上限子棋盘 if (dr < tr + s && dc >= tc + s) { TileBoard(board, tr, tc +s , dr, dc, s, ref number); } else { board[tr + s - 1][tc + s] = t; // 覆盖左下角 TileBoard(board, tr, tc+s, tr + s - 1, tc + s , s, ref number); } // 覆盖四分之一左下限子棋盘 if (dr >= tr + s && dc < tc + s) { TileBoard(board, tr +s, tc, dr, dc, s, ref number); } else { board[tr + s][tc + s -1] = t; // 覆盖右上角 TileBoard(board, tr +s, tc, tr + s, tc + s -1, s, ref number); } // 覆盖四分之一右下限子棋盘 if (dr >= tr + s && dc >= tc + s) { TileBoard(board, tr + s, tc + s, dr, dc, s, ref number); } else { board[tr + s][tc + s] = t; // 覆盖左上角 TileBoard(board, tr + s, tc + s, tr + s, tc + s, s, ref number); } }
3. 二分归并排序
// 二路归并排序算法的实现 public static void MergeShort(int[] array) { int increaseMent = 1; while (increaseMent < array.Length) { Merge(array, increaseMent); increaseMent <<= 1; } } // 一趟二路归并排序算法的实现 public static void Merge(int[] array, int increaseMent) { int[] tempArray = new int[array.Length]; int lastIndex = array.Length - 1; int l1 = 0; //第1个有序表的起始位置 int h1 = 0; //第1个有序表的结束位置 int l2 = 0; //第2个有序表的起始位置 int h2 = 0; //第2个有序表的结束位置 int m = 0; //临时表的初始位置 // 注意这里的临界条件(l2要存在,L2的index是: l1 + increaseMent<=lastIndex) while (l1 + increaseMent <= lastIndex) { l2 = l1 + increaseMent; h1 = l2 - 1; h2 = l2 + increaseMent -1 < lastIndex ? l2 + increaseMent -1 : lastIndex; int i = l1; int j = l2; //两个有序表中的记录没有排序完 while (i <= h1 && j <= h2) { //第1个有序表记录的关键码小于第2个有序表记录的关键码 if (array[i] < array[j]) { tempArray[m++] = array[i++]; } else //第2个有序表记录的关键码小于第1个有序表记录的关键码 { tempArray[m++] = array[j++]; } } //第1个有序表中还有记录没有排序完 while (i <= h1) { tempArray[m++] = array[i++]; } //第2个有序表中还有记录没有排序完 while (j <= h2) { tempArray[m++] = array[j++]; } l1 = h2 + 1; } //原顺序表中还有记录没有排序完 while (l1 <=lastIndex) { tempArray[m++] = array[l1++]; } //临时顺序表中的记录复制到原顺序表,使原顺序表中的记录有序 for (int i = 0; i < array.Length; i++) { array[i] = tempArray[i]; } }
4. 快速排序
// 快速排序(分而治之) public static void QuickShort(int[] array, int low, int high) { int i = low; int j = high; int tempItem = array[low]; while (low < high) { while (array[high] > tempItem && high > low) { high--; } array[low] = array[high]; while (array[low] <= tempItem && low < high) { low++; } array[high] = array[low]; } array[low] = tempItem; if (i < low - 1) { QuickShort(array, i, low - 1); } if (low + 1 < j) { QuickShort(array, low + 1, j); } }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号