2019.01.07-bzoj3309: DZY Loves Math-dtoj1669

 题目描述：

对于正整数n，定义f(n)为n所含质因子的最大幂指数。例如f(1960)=f(2^3 * 5^1 * 7^2)=3, f(10007)=1, f(1)=0。
给定正整数a,b，求sigma(sigma(f(gcd(i,j)))) (i=1..a, j=1..b)。

算法标签：数论，欧拉函数

思路：

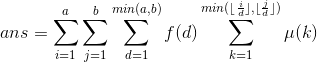
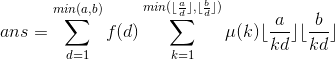
此时预处理出f效率是nlogn还是过不去...真可怕

于是继续化，令T=kd

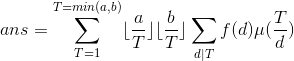
不妨令

 

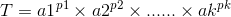
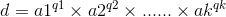
对于存在pi!=pj

如果存在p1-q1>=1，则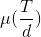为0，不考虑。

其余对于存在一个的情况，你选定一个最大值，对于最大值相同的取正负号的数量相同，因此权值为0.

对于任意pi==pj的情况，取正负号的方案相同，但是其中一组最大值为p1,不为p1+1所以不能完全消去，因此获得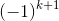的权值

线性筛预处理出f,然后每次log求出答案即可。

以下代码：

#include<bits/stdc++.h>
#define il inline
#define _(d) while(d(isdigit(ch=getchar())))
using namespace std;
const int N=1e7,M=1e7+5;
int mx[M],num[M],pri[N],g[M],tot;bool vis[M];
il int read(){int x;char ch;_(!);x=ch^48;_()x=(x<<1)+(x<<3)+(ch^48);return x;}
il void init(){
    for(int i=2;i<=N;i++){
        if(!vis[i])pri[++tot]=i,vis[i]=1,mx[i]=i,num[i]=1,g[i]=1;
        for(int j=1;j<=tot&&pri[j]*i<=N;j++){
            vis[i*pri[j]]=1;
            if(i%pri[j]==0){
                num[pri[j]*i]=num[i]+1;
                mx[i*pri[j]]=mx[i]*pri[j];
                int tmp=i/mx[i];
                if(tmp==1)g[i*pri[j]]=1;
                else g[i*pri[j]]=(num[tmp]==num[i*pri[j]])?-g[tmp]:0;
                break;
            }
            mx[i*pri[j]]=pri[j];num[i*pri[j]]=1;g[i*pri[j]]=(num[i]==1)?-g[i]:0;
        }
    }
    for(int i=2;i<=N;i++)g[i]+=g[i-1];
}
int main()
{
    init();int T=read();
    while(T--){
        int a=read(),b=read();int pos;long long ans=0;
        for(int i=1;i<=min(a,b);i=pos+1){
            pos=min(a/(a/i),b/(b/i));
            ans+=1ll*(g[pos]-g[i-1])*(a/i)*(b/i);
        }
        printf("%lld\n",ans);
    }
    return 0;
}