LeetCode:字符串（二）

本组囊括字符串相关题目，难度均为简单。

20. Valid Parentheses

注：此题也归为栈类。

题目描述：简单

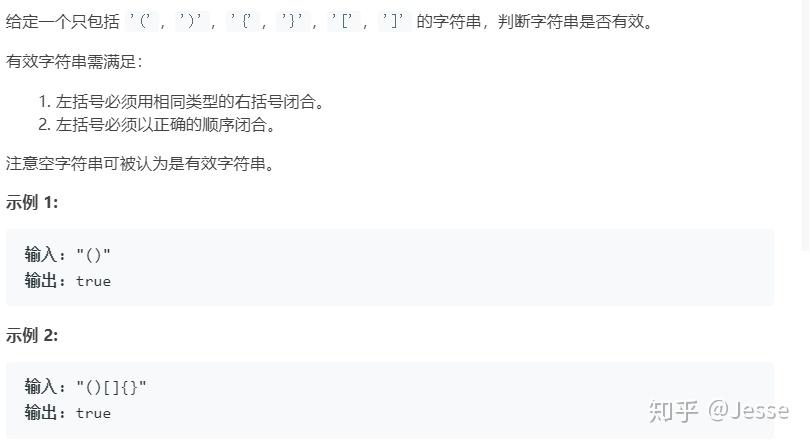
使用栈这一数据结构完成本任务，把开括号按顺序放入栈顶，每遇到一个闭括号，就弹出栈顶元素，看是否和此闭括号匹配。遍历完字符串后若栈为空，则说明都匹配，返回true，反之则返回false.
建立哈希表 dic 构建开闭括号对应关系：key为左括号，value为右括号；这样查询 2 个括号是否对应只需 O(1) 时间复杂度；建立栈 stack，遍历字符串 s 并按照上面算法一一判断。

class Solution:
    def isValid(self, s: str) -> bool:
        stack = []
        mapping = {')':'(', ']':'[', '}':'{'}
        
        for char in s:
            if char in mapping:
                if stack:
                    top_element = stack.pop()
                else:
                    top_element = '#' # 如果stack为空，pop操作会报错，给element赋一个无意义值。
            
                if mapping[char] != top_element:
                    return False
            else:
                stack.append(char)
        # 如果最后栈为空，则原始字符串为空或者括号都能匹配，则返回真；如果栈非空，则返回假。
        return not stack

时间复杂度：O(N),N为字符串长度，for循环内的操作都在O(1)时间内完成。

空间复杂度：O(N),哈希表和栈使用的线性空间的大小。

 

28. Implement strStr()

题目描述：简单

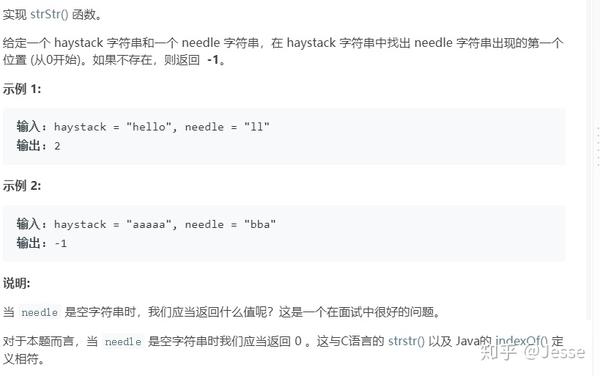
我的理解是实现indexOf()的用法，肯定不能调用类似的库函数啦；

 

官方解法一：

滑动窗口法，看到子串，考虑滑动窗口

class Solution:
    def strStr(self, haystack: str, needle: str) -> int:
        # 官方解法一：滑动窗口法，看到子串，考虑滑动窗口
        # m = len(haystack)
        # n = len(needle)
        # for i in range(m-n+1): # 子串长度为n
        #     if haystack[i:i+n] == needle:
        #         return i
        # return -1

时间复杂度：O((M-N)*N),内层每次比较N个，外层循环M-N次，

空间复杂度：O(1)。

 

官方解法二：双指针

不能用字符串函数，使用双指针pm和pn。

class Solution:
    def strStr(self, haystack: str, needle: str) -> int:
        m, n = len(haystack), len(needle)
        if n == 0:
            return 0
        pm = 0
        while pm < m - n + 1:
            while pm < m - n + 1 and haystack[pm] != needle[0]:
                pm += 1       
            pn, current_len = 0, 0
            while pn < n and pm < m and haystack[pm] == needle[pn]:
                pm += 1
                pn += 1          # 最后为长度n
                current_len += 1 # 最后为长度n
            if current_len == n:
                return pm-current_len
            pm = pm - current_len + 1
        return -1

时间复杂度最坏情况仍然和上面一样。

 

38. Count and Say

题目描述：简单

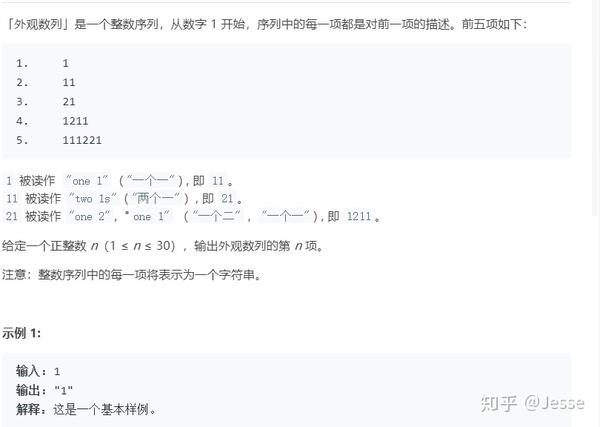
解法一：参考 力扣

循环含义：

每次外循环含义为给定上一个人报的数，求下一个人报的数；每次内循环为遍历上一个人报的数

具体思路：

先设置上一人为'1'；

开始外循环；

每次外循环先置下一人为空字符串，置待处理的字符num为上一人的第一位，置记录出现的次数为1；

开始内循环，遍历上一人的数，如果数是和num一致，则count增加。

若不一致，则将count和num一同添加到next_person报的数中，同时更新num和count；

别忘了更新next_person的最后两个数为上一个人最后一个字符以及其出现次数！

class Solution:
    def countAndSay(self, n: int) -> str:
        # 参考jimmy00745的解法，使用两重循环求解。
        prev_person = '1'
        for i in range(1, n):
            count, num, next_preson = 1, prev_person[0], ''
            for j in range(1, len(prev_person)):
                if num == prev_person[j]:
                    count += 1
                else:
                    next_preson += str(count) + num # 先将第一个不同的数和其计数器加入到next_person最左边，再更新num为下一个数
                    num = prev_person[j]
                    count = 1  # 重置num和count
            # 内层循环完更新next_person和prev_person
            next_preson += str(count) + num
            prev_person = next_preson
        return prev_person

时间复杂度：O(N²)

空间复杂度：O(1)