Python-数据结构之set（集合）

阅读目录：

　　1、集（set）

　　2、set的元素

　　3、set增加

　　4、set删除

　　5、set修改、查询

　　6、set 和线性结构

　　7、集合

　　8、集合运算

　　9、练习题

 

  1、集（set）

　　 约定：

　　　　set翻译为集合

　　　　colection 翻译为集合类型，是一个大概念

　　set：可变，无序，不重复，可迭代的元素集合（一般一个容器都是可以迭代的，例如一个箱子里的东西都可以一个个拿出来）

s = set(range(7))
s # {0, 1, 2, 3, 4, 5, 6]
# s = {} 这是空字典
# s = set() 定义空set只能这样
s1 = set('abc')
s1 # {'a', 'b', 'c'}

s2 = set('a' * 4) # 去重
s2 # {'a'}

s3 = {1,2,3,1,2,3}
s3 # {1, 2, 3}

s4 = {1,'a',(12,3)}
s4 # {(12, 3), 1, 'a'} # 无序，事实上，无序只是看起来无序，但是计算机内部是不可能五的

 

2、set的元素

• set的元素要求必须是可以hash的，也就是说不可变的，如：list，set，dict都不能作为set的元素
• 元素不可以索引，无序
• set 可以迭代　
• s = {1,2,3,(1,2,[4,5],3)} 这样也是错误的！　　

3、set增加：

　　add（elem）:返回None

　　　　增加一个元素到set中，如果元素存在，什么都不做。

　　update(*others):

　　　　合并其他元素到set集合中，参数others 鄙俗是可迭代对象，就地修改

s2.add(3)
s2.add('dassda')
s2.add('ad')
s2 # {3, 'a', 'ad', 'dassda'}


s3 = s2
s3.update([1,2])# 可迭代对象
s3 # {1, 2, 3, 'a', 'ad', 'dassda'}

s3.update({'a','c','f'})
s3 # {1, 2, 3, 'a', 'ad', 'c', 'dassda', 'f'}

　　哈希：hash() 内建函数：如果参数不变，那么哈希值是定值。

　　　　哈希的时间复杂度是O(1) 一步到位，例如，找某人，直接算出这个人的哈希值，可以去找房间号。

4、set删除：

　　　remove（elem）--> None

　　　　从set中移除一个元素，元素不存在，抛出KeyError异常。　　　　

　　　　不需要遍历，因为可以hash，很快就找到，但是频繁的对其删，增，代价要高，但是比list中的代价低多了（无序的）。

　　　discard（elem）---> None

　　　　从set中移除一个元素，元素不存在，什么都不做

　　　pop() --->item

　　　　移除并返回任意的元素，空集返回KeyError

　　　clear()；移除所有元素

5、set修改、查询

　　修改：

　　　　要么删除，要么加入新元素，没有必要修改。

　　查询：非线性解构，无法查询

　　遍历：迭代所有的元素

　　成员运算符：in ，not in 

　　　　　　#在set中效率要高很多，set中的元素是可hash，但是列表就不要用了。set的时间是用空间换来的，因为数据是散列的！

　　　　　　意思就是 提供一个非常大的散列空间，即便只有两个元素！

　　

 

6、set 和线性结构：

　　线性结构的查询时间复杂度是O(n)，即随着数据规模的增大而增加消耗

　　set, dict 等结构，内部使用hash值 作为key，时间复杂度可以做到O(1)，查询时间和数据规模无关。

 

　　可hash：

　　　　数值型int ,float, complex

　　　　布尔型True, False

　　　　字符串string

　　　　元组 tuple

　　　　None

　　　　以上都是不可变类型，称为可哈希类型

7、集合：

　　基本概念：

　　　　全集：

　　　　　　所有元素的结合。例如实数集，所有实数组成的结合就是全集

　　　　子集subset 和超集 superset

　　　　真子集 和 真超集：

　　　　　　A 是B 的子集，且A 不等于B ，A 就是B 的真子集，B 是A的真超集

　　　　并集：多个集合合并的结果

　　　　交集：多个集合的公共部分

　　　　差集：集合中出去喝其他集合公共部分。

8、集合运算：

　　　并集：

　　　　　将两个几个A 和B 的所有的元素合并到一起，组成的结合称为集合A 和集合B 的并集

　　　　　union(*others)：返回和多个集合合并后的新的集合。

　　　　　| ：运算符

　　　　　update(*others)： 和多个集合合并，就地修改

　　　　　|= ：运算符

s = set(range(1,7))
s1 = set(range(3,7))
n = s | s1  # {1, 2, 3, 4, 5, 6}
m = s1.union(s) # {1, 2, 3, 4, 5, 6}

s |= s1 # 此时s 变为  {1, 2, 3, 4, 5, 6}
s

 

　　  

　　　交集：

　　　　　　集合A 和B ，由 所有属于A 且属于B 的元素组成的集合

　　　　　　intersection(*others) ：返回和多个集合的交集

　　　　　　&：运算符

　　　　　　intersection-update(*others) :获取和多个集合的交集，并就地修改

　　　　　　&= ：运算符

s1 = set(range(1,5))
s2 = set(range(4,8))
n = s1.intersection(s2)
print(n) # {4}

s1 &= s2
print(s1) # 此时的s1 {4}

　　　差集：

　　　　　　集合A 和B ，由所有属于A 且不属于B 的元素组成的集合。

　　　　　　difference(*others)：返回和多个集合的差集

　　　　　　- ： 运算符

　　　　　　difference_update(*others )：获取和多个集合的差集并就地修改

　　　　　　-= ：运算符

s1 = set(range(1,5))
s2 = set(range(4,8))
n = s1.difference(s2) # 是S1 - S2
n # {1, 2, 3}

s1 -= s2
s1 # {1, 2, 3}

　　　对称差集：

　　　　　　集合A 和B，由所有不属于A 和B  的交集元素组成的结合，记做：（A - B）U (B - A）

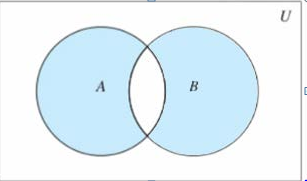
　　　　　　symmetric_difference(other)：返回和一个集合的差集

　　　　　　^ ：运算符

　　　　　　symmetric_differece_update(other):获取和另一个集合的差集并就地修改

　　　　　　^= : 运算符　　　　　　

s1 = set(range(1,5))
s2 = set(range(4,8))
s1 ^ s2 # {1, 2, 3, 5, 6, 7}

s1 ^= s2
s1,s2 # ({1, 2, 3, 5, 6, 7}, {4, 5, 6, 7})

 

 

　　issubset(other)   ：判断当前集合是否是另一个集合的子集   (  <=  )   

　　set1 < set2 ：判断set1 是否是set2的真子集

　　issuperset(other) ： 判断当前集合是否是other的超集 ( >=  )

　　set1 > set2 ：判断set1 是否是set2 的真超集

　　isdisjoint（other）：当前集合和另一个集合没有交集，没有交集返回True　

s1 = set(range(1,5))
s2 = set(range(4,8))
s3 = {1,2}
s4 = set(range(6))
s3.issubset(s1) # True
s4 > s1 # True

 

 

 

 

9、练习题：

　　随机产生2组10个数字列表

　　　　每个数字取值 [10 ,20 ]

　　　　统计20个数字中一共有多少个不同数字？

　　　　2组之间，不重复的数字有几个，分别是什么？

import random

s1 =  set([random.randrange(10,21) for _ in range(10)]) 
s2 =  set([random.randrange(10,21) for _ in range(10)])
print(s1,s2)
a = s1.symmetric_difference(s2)
print(a)

c = s1 & s2
print(c)

s1.update(s2)
print(s1)