Week 7 - 714. Best Time to Buy and Sell Stock with Transaction Fee & 718. Maximum Length of Repeated Subarray

714. Best Time to Buy and Sell Stock with Transaction Fee - Medium

Your are given an array of integers prices, for which the i-th element is the price of a given stock on day i; and a non-negative integer fee representing a transaction fee.

You may complete as many transactions as you like, but you need to pay the transaction fee for each transaction. You may not buy more than 1 share of a stock at a time (ie. you must sell the stock share before you buy again.)

Return the maximum profit you can make.

Example 1:

Input: prices = [1, 3, 2, 8, 4, 9], fee = 2
Output: 8
Explanation: The maximum profit can be achieved by:
Buying at prices[0] = 1
Selling at prices[3] = 8
Buying at prices[4] = 4
Selling at prices[5] = 9
The total profit is ((8 - 1) - 2) + ((9 - 4) - 2) = 8.

Note:

• 0 < prices.length <= 50000.

• 0 < prices[i] < 50000.

• 0 <= fee < 50000.

My Solution:

#include<vector>
#include<iostream>
using namespace std;
class Solution {
public:
  int maxProfit(vector<int>& prices, int fee) {
    int p1 = 0, p2 = INT32_MIN;
    for (int i = 0; i < prices.size(); i++) {
      int temp = p1;
      p1 = max(p1, p2 + prices[i]);
      p2 = max(p2, temp - prices[i] - fee);
    }
    return p1;
  }
  
  int max(int i, int j) {
    if (i >= j) return i; else return j;
  }
};

这道题主要的思想是动态规划，难点在于如何想到用两个状态来进行迭代。用一次循环扫整个价格数组，用p1记录无库存状态下的利润，p2记录有库存状态下的利润，当买入时更新p2，卖出时更新p1。

718. Maximum Length of Repeated Subarray - Medium

Given two integer arrays A and B, return the maximum length of an subarray that appears in both arrays.

Example 1:

Input:
A: [1,2,3,2,1]
B: [3,2,1,4,7]
Output: 3
Explanation: 
The repeated subarray with maximum length is [3, 2, 1].

Note:

• 1 <= len(A), len(B) <= 1000
• 0 <= A[i], B[i] < 100

my solution：

#include<vector>
#include<iostream>
using namespace std;
class Solution {
public:
  int findLength(vector<int>& A, vector<int>& B) {
    vector<int> D(B.size()+1, 0);
    vector<vector<int>> C(A.size() + 1, D);
    int res = 0;
    for (int i = 0; i < A.size(); i++) {
      for (int j = 0; j < B.size(); j++) {
        if (A[i] == B[j]) {
          C[i + 1][j + 1] = C[i][j] + 1;
        }
        if (C[i + 1][j + 1] > res) res = C[i + 1][j + 1];
      }
    }
    return res;
  }
};

考虑这样一个表格：

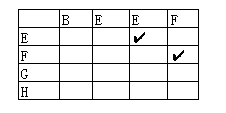
如果两个字符串中有一个子串相同，那么在这个表格中，这个子串就会以斜线的方式显示。利用这个性质对子串的长度计数，就可以得到这道题的动态规划解。