基于线性判别分析的维数约简
最近大四还有个必修:课程设计。选到的题目是 'Fisher辨别分析用于人脸数据维数约简的实现'。
然后在Scikit learn中找到了相关的python库: Dimensionality reduction using Linear Discriminant Analysis
/*************************************************************************************************************************************************************************************************************************/
判别分析中的线性判别分析可以用来进行有监督的维数约简,他将输入数据投影到线性子空间。其中的投影方向能达到最好的分类效果。约减后的维数小于数据的类别数,所以这是一个很好的降维,而且只在多类问题下有效。
该方法 在模块中的discriminant_analysis.LinearDiscriminantAnalysis.transform。
期望的维数可以通过 n_components 参数来设置。该参数不会影响
discriminant_analysis.LinearDiscriminantAnalysis.fit 或者discriminant_analysis.LinearDiscriminantAnalysis.predict.
例子:
LDA和QDA的数学描述
线性判别分析和二次判别分析都可以由简单的概率模型得来,此概率模型对各个类的类条件概率P(X|y=k)。根据贝叶斯公式,后验概率为:
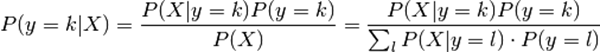
通过最大化后验概率即可得到类别。
具体来看,对于LDA和QDA,类条件概率密度可以建模为多维高斯分布,他的概率密度为:

为了使用该概率模型进行分类,我们只需要从训练数据中估计某一类K的类先验概率P(y=k),类均值μk(样本类均值),相关系数矩阵(要么是通过样本的相关矩阵,要么是正则化估计:参见shrinkage部分)

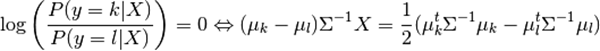
对于二次判别分析,对于协方差没有要求。详细见
LDA的数学描述
为了理解LDA在维数约简中的运用,对LDA分类准则的几何描述十分有用(上面的那一part)。设类别总数为K。在LDA中我们假设过所有类的协方差矩阵都相同。重新调整数据而且该协方差作为特征(还有疑问):
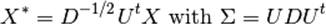

我们还可以进一步约减维数,对于给定的L,通过映射到能最大化类间距离的子空间Hl(实际上我们在进行PCA对于映射后的类均值)。L就是对应n_components参数在discriminant_analysis.LinearDiscriminantAnalysis.transform方法中。具体见此
Shrinkage
收缩是一个改善协方差矩阵估计的工具,当训练样本数相对于数据维数(特征)比较小时。在这种情况下,经验样本协方差是一个不好的估计。Shrinkage LDA可以把
Shrinkage 参数设置为"auto"。这样就可以自动决定最优的收缩参数(按照Ledoit and Wolf提出的定理)。注意收缩只在将solver 参数设为'lsqr' or 'eigen'时起作用。
收缩参数也可以手动设置为0-1之间的数。这样在两个极端情况之间就是收缩版的协方差矩阵。下图给出了实际的差别:是否有收缩操作
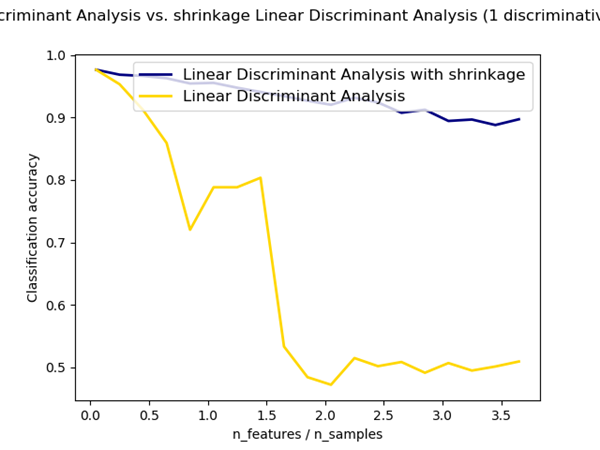
Estimation algorithm 估计算法
默认的解决方法是'svd'。它既能用来分类也能变换,而且他不依靠协方差矩阵的计算。这在维数很高时是一个优势,但他不支持shrinkage。
'lsqr'只能用于分类,支持shrinkage
'eigen'是基于类间/类内比值(广义瑞雷商)的最大化,即能分类也能转换,可以支持shrinkage。但是他需要计算协方差矩阵,所以它适用于高位特征的情况。
Examples:
Normal and Shrinkage Linear Discriminant Analysis for classification: Comparison of LDA classifiers with and without shrinkage.
References:
|
[3] |
(1, 2) "The Elements of Statistical Learning", Hastie T., Tibshirani R., Friedman J., Section 4.3, p.106-119, 2008. |
|
Ledoit O, Wolf M. Honey, I Shrunk the Sample Covariance Matrix. The Journal of Portfolio Management 30(4), 110-119, 2004. |



