简明数学笔记

1，常见的数学符号及含义

为什么要使用数学符号？因为数学符号是简洁的，表义的，准确的。

 

2，求和

 

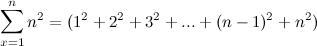
3，方差(variance)

方差是实际值(r)与标准值(s)差的平方，即(r-s)^2

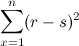
方差和反映的是数据的波动程度，方差和越小，数据波动越小，越稳定。

 

4，导数(derivative)

微分学是微积分的重要组成部分，基本概念是导数和微分。

*导数，研究函数在某点变化的快慢，即变化率问题。

*微分，研究当自变量变化少许时，函数变化了多少，即改变量问题。

 

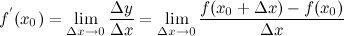
常用求导公式：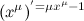

 

5，贝叶斯概率公式(Bayes' theorem)

P(A|B)是指：在B发生的情况下，A发生的可能性。贝叶斯是很智能的概率算法，他根据已知学习来的值，来求未知概率。

 

比如邮件过滤：

B        =>邮件中包含ad

A        =>邮件是垃圾邮件

P(B)    =>垃圾邮件(占全部邮件)的概率(以前学习得到的概率。比如在20份邮件中，有1份是垃圾邮件，P(B)=1/20，即垃圾邮件的概率是0.05)

P(A)    =>所有邮件包含ad的概率(以前学习得到，比如40份邮件中，只中1份包含ad，则为1/40=0.025

P(B|A) =>如果邮件是垃圾邮件，那么包含ad的可能性。(以前学习得到，有10份垃圾邮件，其中有5分包含了ad,即5/10=0.5

 

P(A|B) =>如果现在有一个邮件中包含了ad,那么这份邮件是垃圾邮件的概率就可以求出：

P(A|B) = P(B|A)*P(A)/P(B) = 0.5*0.025/0.05 = 0.25

 

6，排列(Permutation或Arrangement)

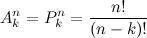
从n个元素中拿出k个来进行排列，这个时候顺序是影响结果的。在老教材上用的是P(Permutation)来表示，但在新教材用的是A(Arrangement)。

比如，你从n=5个元素中挑k=3个，其有5!/(5-3)!=60种结果。

 

7，组合(Combination)

组合与排列的唯一不同就是：取出的元素不考虑顺序。

比如，你从n=5个元素中取出k=3个，5!/3!*(5-3)!=10

 

注意:

a,上下标读法是从上向下读的，即C,5,4的写法是：

b,0!=1, 1!=1, 2!=2*1=2