数字签名与加密解密
有关数字签名与加密解密的文章我看了许多次,基于这样的事实——我总是说服不了自己,所以每次看都看不明白,说服不了自己。最近在看OAuth的相关东西,数字签名与加密解密是绕不开了,干脆静下心来,看看资料,尝试着将自己说服.
1,加密解密基础
简单地讲,计算机加密无非是,用密钥K,对明文P加密,得到密文M:
K(P) = M
解密就是将这个过程反过来:
K(M) = P
对于密钥K,有两种选择方式:对称加密,不对称加密。
a,对称加密: 加密解密,都用同一个Key
b,不对称加密:加密解密用不同的Key(密钥对VK和SK),比如加密用VK,则解密用SK。反之亦然,如果你用SK加密,则用VK来解密。
2,数字签名
数字签名实际上起到两个作用:1,验证。2,加密。
这里的验证指的是,验证发送消息人的身份,以防伪造者。而加密指的是将明文加密,以防被偷看。
数字签名既可以用"对称加密"来实现,也可以用"不对称加密"来实现。
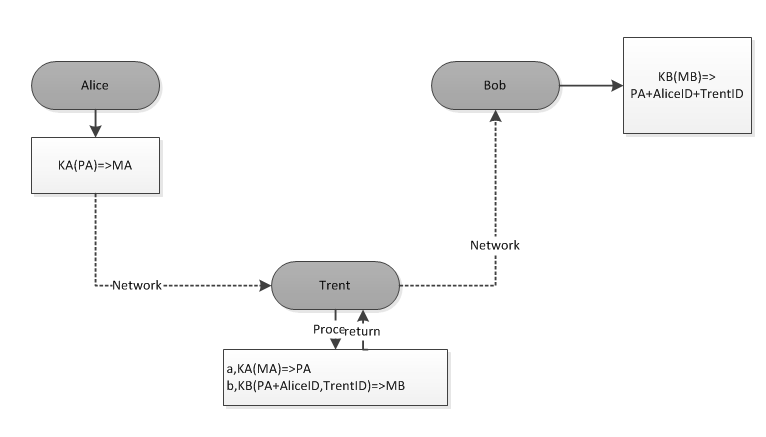
3,采用对称加密来实现数字签名
说明:
a,使用对称加密(加密,解密使用相同的密钥)。
b,需要第三方仲裁者
资源:
a,两个密钥(记住,加密/解密用同一个密钥),分别称之为KA和KB
角色:
Alice: (明文PA,密钥KA,密文MA)
Bob: (明文PB,密钥KB,密文MB)
Trent:同时拥有(KA,KB)
步骤:
a,Alice将明文PA经过密钥KA加密,得到密文MA。
b,Alice将MA传给Trent
c,仲裁者Trent用KA解密MA,得到PA
d,仲裁者Trent用PA加上Alice的身份证,再加上Trent自己的身份证
e,Trent将上面的(AliceID+TrentID+PA),经过密钥KB加密,得到MB。
f,Trent将MB传给Bob
g,Bob用KB来解密MB,得到PA,Alice的身份证和Trent的身份证
备注:
由于在密钥只有Trent知道,在网络上传输的都是密文,所以不怕被偷看。
其次,密钥变换过程是Trent完成的,这里Trent是可信的。所以不存在伪造问题。
什么?Alice不承认发过PA,我找Trent说理去。
4,采用不对称加密实现数字签名
说明:
a,采用不对称加密技术
b,用公钥加密的东西,只有私钥能解开,同样用私钥加密的东西,只有公钥能解开
c,使用两个密钥对(每个密钥对包含公钥/私钥各一个),不需要第三方仲裁就可以完成数字签名
资源:
a,第一对密钥对,公钥VK-A,私钥SK-A
b,第二对密钥对,公钥VK-B,私钥SK-B
角色:
Alice:明文PA,第一对私钥SK-A,VK-A/VK-B
Bob: 第二对SK-B,VK-A/VK-B
Crack:因为公钥是可以公开的,所以Crack很容易搞到了两个公钥VK-A/VK-B,怎么来的?或许是Google得到的吧,谁知道呢。
步骤:
a,Alice先将明文PA用私钥SK-A加密(这一步起到防抵赖的作用,只有Alice有私钥SK-A)
b,Alice再将上面的结果用公钥VK-B加密(这一步起到加密的作用,只有Bob的私钥SK-B能解开)
c,Alice将经过上面步骤得到的密文MA,发给Bob
d,防不胜防啊,有人想偷看,结果愣是没有看懂(嘿嘿,只有Bob有SK-B这个神器)
e,还有人想伪造,好吧,算你狠,你能得到公钥,所以你能产生VK-A(X),VK-B(X)
f,Bob收到了三个东西:MA,VK-A(X)和VK-B(X)
g,先用自己的私钥SK-B(MA)=>SK-A(PA), 然后再用公钥VK-A(SK-A(PA))=>PA,哈哈,Alice来消息了。
h,VK-A(X),什么东西?先用SK-B试试,啥也看不到嘛!
I, VK-B(X),啥东西?先用SK-B解开看看,原来是X啊。再用VK-A试试,啥也看不到嘛,肯定不是Alice。(记住VK-A只能解Alice的私钥SK-A加密的内容,别人没有SK-A)
备注:
信息在网络上传输都是加密过的,不怕被偷看。
什么?你有VK-A,能看到Alice经过私钥加密的东西,但他妈的Alice每次发送的都是经过VK-B加密过的密文。
由于Alice发送的东西经过自己的私钥SK-A和Bob的公钥VK-B同时加过密,不怕被伪造(没有私钥,咋造啊),不怕被抵赖(只有你Alice才能用SK-A加密,我用VK-A解开的东西,肯定是你Alice发的)。
参考资料:
http://www.ruanyifeng.com/blog/2006/12/notes_on_cryptography.html