一.查找表(Look-Up-Table)的原理与结构
采用这种结构的PLD芯片我们也可以称之为FPGA:如altera的ACEX,APEX系列,xilinx的Spartan,Virtex系列等。
查找表(Look-Up-Table)简称为LUT,LUT本质上就是一个RAM。 目前FPGA中多使用4输入的LUT,所以每一个LUT可以看成一个有4位地址线的16x1的RAM。 当用户通过原理图或HDL语言描述了一个逻辑电路以后,PLD/FPGA开发软件会自动计算逻辑电路的所有可能的结果,并把结果事先写入RAM,这样,每输入一个信号进行逻辑运算就等于输入一个地址进行查表,找出地址对应的内容,然后输出即可。
下面是一个4输入与门的例子,
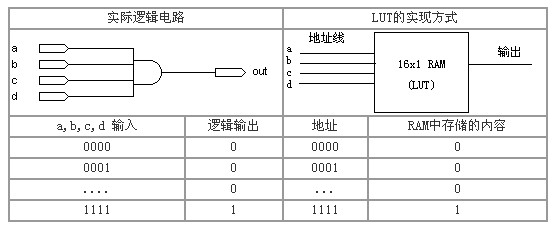
(转载自:http://www.fpga.com.cn/advance/structures/lut.htm)
二.FPGA教程之LUT与逻辑的联系
一般低成本的FPGA(如Cyclone系列,Spartan系列)由4输入的LUT表完成组合逻辑的功能,即相当于一个16bit存储空间,4bit地址输入,1bit输出的RAM,我们通过配置者16bit的空间完成任意一个“四输入一个输出的逻辑表达式”;如我们需要完成Out = ABCD(四输入与门),配置数据为“0x8000”,即当查找地址“4b’1111”,RAM的输出为1,否则为零。
假如我需要实现一个加法器,并输出它的进位值Carry,分别用逻辑电路和配置数据表示?
如果我们只有三个输入值,LUT的输入又该如何完成?
在数字电路中,信号的传递会出现延迟,延迟有逻辑门本身造成的,由于逻辑门中的三极管在传输信号时存在延迟;延迟也会因外部电路的分布电容而产生,所以逻辑门的输出信号要滞后输入信号。
与非门平均传输延迟时间是指一个数字信号从输入端输入,经过门电路再从其输出端输出所延迟的时间,它反映了电路传输信号的速度。
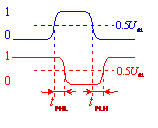
为了测试方便,都以电压波形摆幅的二分之一处为起始点去测量平均延迟时间。从输入上升边50%到输出下降边50%为止的时间叫做导通延迟时间tPHL;从输入下降边50%到输出上升边50%为止的时间叫做截止延迟时间tPLH。导通延迟时间和截止延迟时间的平均值称为平均延迟时间(如上图)
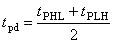
标准TTL门的平均传输延迟时间的典型值约10ns。
本身任何数字电子技术都是基于TTL技术发展起来的,当然,当今数字技术以CMOS技术为主,所以本身LUT从地址输入到存储值的输出也存在延迟,这也是影响FPGA工作频率的重要因素,随着技术的不断进步,该延迟对FPGA工作频率并不起着关键的作用。
现在我们举个更复杂的例子,两个32-bit数据的比较器:
从逻辑表达式上来看,我们需要作如下步骤:
temp[31..0] = ain[31..0] xor bin[31..0];
equal = not (temp[31] or temp[30] … or temp[1] or temp[0]);
以下是用VHDL实现,并用FPGA实现的方式:
library ieee;
use ieee.std_logic_1164.all;
use ieee.std_logic_unsigned.all;
use ieee.std_logic_arith.all;
entity comparator_32b is
port(
ain: in std_logic_vector(31 downto 0);
bin: in std_logic_vector(31 downto 0);
equal: out std_logic;
great: out std_logic
);
end comparator_32b;
architecture synlogic of comparator_32b is
begin
equal <= '1' when ain = bin else '0';
-- great <= '1' when ain > bin else '0';
end synlogic;
在综合报告中可以知道,它需要21个逻辑资源即LUT;如下图:

描述一下“great <= '1' when ain > bin else '0';”的综合流程?
经过上述描述,我们可以知道FPGA的综合流程,即根据你描述的逻辑功能,将逻辑分成若干个步骤,让它们适用于在LUT中完成,然后为每个LUT生成配置数据,通过连接每个LUT,最终完成逻辑功能。也许你也看得出来,从{ temp[31..0] = ain[31..0] xor bin[31..0] equal = not (temp[31] or temp[30] … or temp[1] or temp[0])}到LUT,虽然它们完成都是相同的功能,但是从它们所耗费的逻辑门有很大的差距,如果直接用逻辑表达式,我们需要31个XOR门,30个OR门,而每个LUT的每个bit等效于4个门,即4门/bit;所以FPGA需要21*16*4个门,从逻辑成本上FPGA无法像ASIC一样大批量的生产,但是FPGA的可配置性,使得它允许你在设计可以有错误,而不像ASIC,流片出来后就无法修改,而每次流片所需要的费用已经达到100万美元(65nm),是中小企业无法承受的费用,如果错误的设计流入市场,所产生的维护费用更是难以估量,例如,Nvidia在第二季度一次性支出1.96亿美元,用来解决用于笔记本电脑的某些型号的上一代MCP(媒体通信处理器)和GPU(图形处理器)产品之“核心与封装材料不足”的问题;从而造就FPGA在很多专业领域的流行。
(转载自:http://blog.ednchina.com/wind330/194115/message.aspx)
二.FPGA的逻辑单元与门对应关系
一般而言FPGA等效门数的计算方法有两种,一是把FPGA基本单元(如LUT+FF,ESB/BRAM)和实现相同功能的标准门阵列比较,门阵列中包含的门数即为该FPGA基本单元的等效门数,然后乘以基本单元的数目就可以得到FPGA门数估计值;二是分别用FPGA和标准门阵列实现相同的功能,从中统计出FPGA的等效门数,这种方法比较多的依赖于经验数据。
对于第一种方法,FPGA包括LUT/FF/RAM等资源,分析各种资源等效门数时,总原则是等效原则,就是实现相同的功能,在标准门阵列中需要的门数就是FPGA该资源等效门数,例如实现一个带寄存器输出的4输入XOR,在FPGA中需要用一个LUT和1个FF实现,在标准门阵列中一般要用21个与非门实现,于是1个LUT+1个FF等效于21个门。对ESB(BRAM),由于用标准门阵列实现1bit的RAM时一般需要4个门,因此SB/BARM 做RAM使用时,1bit等效4个门,对Altera FPGA中一个2048bit的ESB,等效门数为8K。光靠这些数据还不能比较准确地计算出FPGA的等效门数。因为这只是一种简单情况,实际情况要复杂很多。
例如,如果实现的是带寄存器输出地2输入XOR,FPGA也要用1个LUT+FF,而标准门阵列只需要8个NAND,于是1个LUT+1个FF只等效于8个门。同时特定功能的实现,在不同的标准门阵列系列中需要的门数也不一样,因此等效门的计算只能是个大概的数值。也就是说对于某一具体型号FPGA的门数估计,与FPGA资源的用途有密切关系。LUT用于实现2输入XOR和4输入XOR等效门数不一样(分别为1和13);FF不带异步清零、复位、时钟使能和带这些端口的等效门数不同(分别为8和13);ESB(BRAM)做RAM使用时,1bit等效4个门,1个2048bit的BRAM等效8K门,但是做查找表使用时可能只相当于不到200门。因此估计FPGA的等效门数需要做更细致的分析。
下面以EP20K1000E为例详细说明FPGA等效门数的估计方法。
(1)计算逻辑阵列的等效门数
估算EP20K1000E的门数时,把FPGA特定资源和LCA300K标准逻辑阵列的门数(LSI LCA300K Data Book)比较,可以对FPGA等效门做出估计。FPGA一个LUT+FF等效门数计算如图2所示
即LUT+FF等效于8~21个门,上限和下限分别由实现简单函数、复杂函数分别界定。
APEX20K的等效门数也可以根据经验数据获得,把超过100个针对4输入LUT的设计用FPGA实现,同时用LCA300K gate arrays和Design Compiler实现,比较相同的设计FPGA所用的LE数目和LCA300K所用的门数可知,每个LE相当于12个门。EP20K1000E有38400个LE,于是相当于46万门。
(2)计算ESB的等效门数
RAM中一个bit所需要的门数与RAM的体系结构、工艺、厂商等有关,一般而言,1bit相当于4个门,Altera也采用这个标准,这样可以方便地估计ESB等效门数。
计算ESB等效门数也可以采用和LSI LCA300K比较的方法,即通过与实现相同容量RAM在LCA300K所用的门数相比较,从而得到ESB的每一bit相当于多少门,从而计算出ESB的等效门数,参考图3。
4gates/bit是一个比较合适的估计,于是EP20K1000E的ESB等效门数为 160 ESBs X 2,048 bits per ESB X 4 gates per bit = 1,310,720 gates,即约为130万门。
总而言之,对EP20K1000E,LUT+FF等效门数约为46万(经验数值),ESB全用作RAM时等效门数约为130万,所以最大系统门数为170万。
结论:
FPGA等效门数估计方法可以是把FPGA资源基本单元(如LUT+FF,ESB)和实现相同功能的标准门阵列相比得到FPGA基本单元等效的门数,然后乘以单元的个数得到整个FPGA等效门数。也可以是实现很多设计,和用标准门阵列相比,从中统计出等效门数。
FPGA 的等效门数估计一般分为LUT+FF和ESB(BRAM)两部分,LUT+FF等效于8~21个门,典型值为12;ESB做RAM使用时,一般相当于4门/bit,此时估计出的门数最多,如果ESB做乘积项/LUT则等效门数大大减小,例如对EP20K1000E,前者为130万,后者为2万。
(转载自:http://blog.mcuol.com/User/luozhen0810/Article/9646_1.htm)


