【计算几何】凸包

计算几何-凸包

二维凸包

凸多边形

凸多边形是指所有内角在\(\left[ 0,\pi \right]\)范围内的简单多边形。

凸包

对于在平面上的一个点集，凸包是能包含所有点的最小凸多边形。

其定义为：对于给定集合\(D\)，所有包含\(D\)的凸集的交集\(S\)被称为\(D\)的凸包。

如：

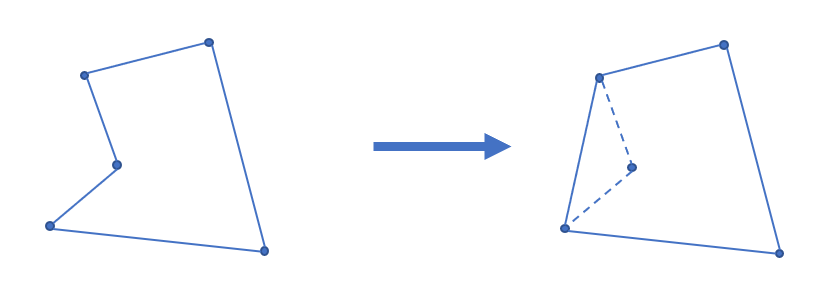
凸包求法

对于平面上的一个点集，其凸包可以用分治，\(Graham-Scan\)，和 \(Andrew\)。

分治

对于分治算法解决凸包问题，递归求解，找到子问题的凸包，讲左右两个子集的凸包进进行合并即可，时间复杂度\(O(n \log n)\)。

\(Andrew\)

对于\(Andrew\)算法，主要流程：

首先将所有点以横坐标为第一关键字，纵坐标为第二关键字进行排序；
显然排序后最小的元素和最大的元素一定在凸包上，然后用单调栈维护上下凸壳；
因为上下凸壳所旋转的方向不同，我们首先升序枚举下凸壳，然后降序枚举上凸壳。

时间复杂度\(O(n \log n)\)。

\(Graham-Scan\)

主要介绍这种算法，更好写一些，首先我们先找出在最右下角的点，此时这个点一定在凸包上，然后我们从这个点开始逆时针旋转，同时用单调栈维护凸包上的点，每加入一个新点是判断改点是否会出现，该边在上一条边的“右边”，如果出现则删除上一个点。时间复杂度\(O(n \log n)\).

【模板】二维凸包

Code:

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+10;
int n,top;double ans;
struct geometric{
    double x,y,dss;
    friend geometric operator + (const geometric a,const geometric b){return (geometric){a.x+b.x,a.y+b.y};} 
    friend geometric operator - (const geometric a,const geometric b){return (geometric){a.x-b.x,a.y-b.y};} 
    double dis(geometric a,geometric b){return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));}
    double dot(geometric a1,geometric a2,geometric b1,geometric b2){return (a2.x-a1.x)*(b2.x-b1.x)+(a2.y-a1.y)*(b2.y-b1.y);}
    double cross(geometric a1,geometric a2,geometric b1,geometric b2){return (a2.x-a1.x)*(b2.y-b1.y)-(a2.y-a1.y)*(b2.x-b1.x);}
};
geometric origin,data[maxn],st[maxn];
bool vis[maxn];
bool cmp(geometric a,geometric b)
{
    geometric opt;
    double tamp=opt.cross(data[1],a,data[1],b);
    if(tamp>0)return true;
    if(tamp==0&&opt.dis(data[1],a)<=opt.dis(data[1],b))return true;
    return false;
}
geometric opt;
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%lf%lf",&data[i].x,&data[i].y);
        if(i!=1&&data[i].y<data[1].y)
        {   
            double tmp;
            swap(data[1].y,data[i].y);
            swap(data[1].x,data[i].x);
        }
        if(i!=1&&data[i].y==data[1].y&&data[i].x>data[1].x)
        	swap(data[1].x,data[i].x);
    }
    sort(data+2,data+n+1,cmp);
    st[++top]=data[1];
    for(int i=2;i<=n;i++)
    {
        while(top>1&&opt.cross(st[top-1],st[top],st[top],data[i])<=0)top--;
        st[++top]=data[i];
    }
    st[++top]=data[1];
    for(int i=1;i<top;i++)ans+=opt.dis(st[i],st[i+1]);
    printf("%.2lf",ans);
    return 0;
}

动态凸包

首先我们考虑这样一个问题：

两种操作：

向点集中添加一个点\((x,y)\);

询问点是否在凸包中。

首先我们对于一个动态的凸包，很明显在每次加入新点时不能再进行一次\(Graham-Scan\)，否则时间复杂度不优。

那么我们就可以用一下方法：

首先建一棵平衡树，按极角排序；
询问是找到该点的前驱后继，用叉积判断即可，否则执行插入操作；
插入时，先将点插入平衡树内然后找该点的前驱后继，同时不断去旋转将在凸包内的点删去。

对于平衡树我们可以直接用\(STL\)里的\(set\) 去实现，需要用到迭代器。

Professor's task

Code:

#include<bits/stdc++.h>
#define it set<geometric>::iterator
#define eps 1e-8
using namespace std;
const int maxn=1e5+10;
int Sure(double x){return fabs(x)<eps?0:(x<0?-1:1);}
struct geometric{
    double x,y;
    geometric(double X=0,double Y=0):x(X),y(Y) {}
    friend geometric operator + (const geometric a,const geometric b){return geometric(a.x+b.x,a.y+b.y);} 
    friend geometric operator - (const geometric a,const geometric b){return geometric(a.x-b.x,a.y-b.y);} 
    friend geometric operator * (const geometric a,double p){return geometric(a.x*p,a.y*p);}
    friend geometric operator / (const geometric a,double p){return geometric(a.x/p,a.y/p);}
    double dis(geometric a,geometric b){return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));}
    double dot(geometric a1,geometric a2,geometric b1,geometric b2){return (a2.x-a1.x)*(b2.x-b1.x)+(a2.y-a1.y)*(b2.y-b1.y);}
    double cross(geometric a1,geometric a2,geometric b1,geometric b2){return (a2.x-a1.x)*(b2.y-b1.y)-(a2.y-a1.y)*(b2.x-b1.x);}
    double corner(geometric a1,geometric a2,geometric b1,geometric b2){return dot(a1,a1,b1,b2)/(dis(a1,a2)*dis(b1,b2));}
    double area(geometric a1,geometric a2,geometric b1,geometric b2){return fabs(cross(a1,a2,b1,b2));}
    double angle(geometric a){return atan2(a.y,a.x);}
    geometric rotate_clockwise(geometric a,double theta){return geometric(a.x*cos(theta)-a.y*sin(theta),a.x*sin(theta)+a.y*cos(theta));}
    geometric rotate_counterclockwise(geometric a,double theta){return geometric(a.x*cos(theta)+a.y*sin(theta),-a.x*sin(theta)+a.y*cos(theta));}
}opt,d[maxn],origin;
bool operator < (geometric a,geometric b){
    a=a-origin;b=b-origin;
    double ang1=atan2(a.y,a.x),ang2=atan2(b.y,b.x);
    double l1=sqrt(a.x*a.x+a.y*a.y),l2=sqrt(b.x*b.x+b.y*b.y);
    if(Sure(ang1-ang2)!=0)return Sure(ang1-ang2)<0;
    else return Sure(l1-l2)<0;
}
int q,cnt;
set<geometric> S;
it Pre(it pos){if(pos==S.begin())pos=S.end();return --pos;}
it Nxt(it pos){++pos; return pos==S.end() ? S.begin():pos;}
bool Query(geometric key)
{
    it pos=S.lower_bound(key);
    if(pos==S.end())pos=S.begin();
    return Sure(opt.cross(*(Pre(pos)),key,*(Pre(pos)),*(pos)))<=0;
}
void Insert(geometric key)
{
    if(Query(key))return;
    S.insert(key);
    it pos=Nxt(S.find(key));
    while(S.size()>3&&Sure(opt.cross(*(Nxt(pos)),*(pos),*(Nxt(pos)),key))>=0)
    {
        S.erase(pos);pos=Nxt(S.find(key));
    }
    pos=Pre(S.find(key));
    while(S.size()>3&&Sure(opt.cross(*(Pre(pos)),*(pos),*(Pre(pos)),key))<=0)
    {
        S.erase(pos);pos=Pre(S.find(key));
    }
}
int main()
{
    scanf("%d",&q);
    for(int i=1;i<=3;i++)
    {
        int opt;double x,y;scanf("%d%lf%lf",&opt,&x,&y);
        d[++cnt]=geometric(x,y);origin.x+=x;origin.y+=y;
    }
    origin=origin/3.0;
    for(int i=1;i<=3;i++)S.insert(d[i]);
    for(int i=4;i<=q;i++)
    {
        int opt;double x,y;
        scanf("%d%lf%lf",&opt,&x,&y);
        d[++cnt]=geometric(x,y);
        if(opt==1)Insert(d[cnt]);
        else {
            if(Query(d[cnt]))printf("YES\n");
            else printf("NO\n");
        }
    }
    return 0;
}

注意使用迭代器时不要越界，要和用指针一样小心！