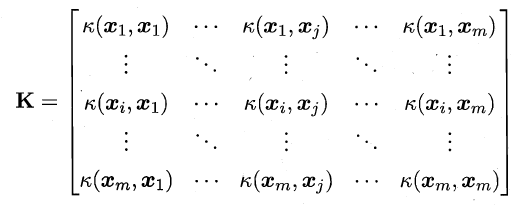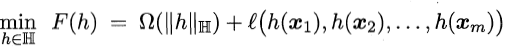支持向量机（Support Vector Machine, SVM）是一种二分类模型。给定训练集D = {(x1,y1), (x2,y2), ..., (xm,ym)}，分类学习的最基本的想法即是找到一个超平面S：
，从而将训练集D的样本空间中不同类别的样本区分开。
SVM的模型，由简至繁地，包括：线性可分支持向量机（linear SVM in linearly separable case）、线性支持向量机（linear SVM）以及非线性支持向量机（non-linear SVM）。
当训练数据线性可分时，SVM试图寻找硬间隔最大化（hard margin maximization）的划分超平面，因为这样的超平面产生的分类结果是最鲁棒的，由此学习的线性分类器称为线性可分支持向量机；而当训练数据近似线性可分时，通过软间隔最大化（soft margin maximization），也可学习得到分类器，称为线性支持向量机；当数据线性不可分时，则可以使用核技巧（kernel methods）以及软间隔最大化，习得非线性支持向量机。“间隔、”核技巧“等相关概念均将在下文中予以阐述。
一、线性可分支持向量机
1.1 间隔与支持向量
如前文所述，划分超平面可以用线性方程来描述，其中ω为法向量，b为位移。于是，划分超平面可以由ω和b确定，记为(ω, b)。利用高中解析几何的相关知识容易推算出，样本空间中任意点到超平面(ω, b)的距离即为
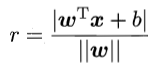
由于若超平面(ω', b')可以对样本正确分类，则对于(xi,yi)，若yi=+1，则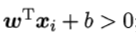
；若yi=-1，则
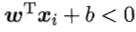。令
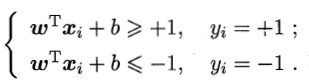
则总存在缩放变换ςω→ω',ςb→b'使得上式成立。由此，定义”支持向量“（support vector）为满足上式且距离超平面最近的点。两个异类支持向量到超平面的距离之和被称为”间隔“（margin），为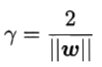
。顺便一提，所谓样本都必须划分正确的情形称为“硬间隔”（hard margin），而“软间隔”（soft margin）则允许某些样本不满足
。
SVM的任务是找到”最大间隔“（maximum margin）的划分超平面。于是，SVM的基本型可以表达为
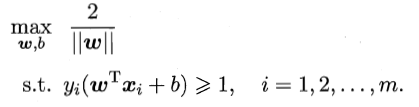
进而可以写为
值得注意的是，间隔貌似只与ω有关，但事实上，b通过约束隐式地影响着ω的取值，进而对间隔产生影响。
1.2 对偶问题与SMO算法
为求解得到最大间隔划分超平面的模型
，一种高效的办法是利用lagrange乘子法得到SVM基本型的”对偶问题“（dual problem），再利用SMO算法求解。
首先，在基本型中，对每条约束添加lagrange乘子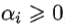
，得到lagrange函数为
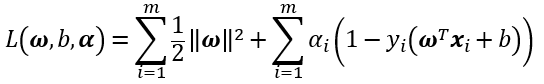
为取到函数的最值，令L(ω,b,α)对ω和b分别求偏导为零，得到
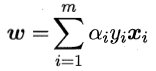
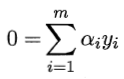
代入L(ω,b,α)，消去ω和b，即得到SVM基本型的对偶问题
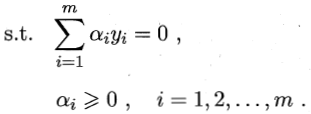
且上述过程需要满足KKT条件，即要求
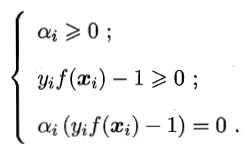
直接用二次规划算法来求解对偶问题，开销较大。比较高效的是SMO算法（Sequential Minimal Optimization）。
SMO首先初始化参数，然后不断执行下述步骤直至收敛：
- 选取一对需要更新的αi和αj；
- 固定αi和αj以外的参数，求解上式获得更新后的αi和αj。
最后，由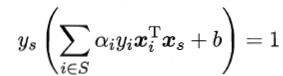
，可以确定偏移项b为
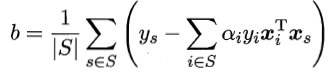
1.3 核函数
如果原始样本空间中不存在可以正确划分样本的超平面，则可以将样本从原始空间映射到更高维的特征空间，使得样本在此特征空间内线性可分。事实上，若原始空间是有限维的，则一定存在一个更高维的空间使样本线性可分。
令Φ(x)表示将x映射后的特征向量，则在特征空间中，划分超平面对应的模型可表示为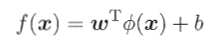
。于是得到基本型
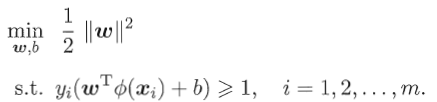
及其对偶问题
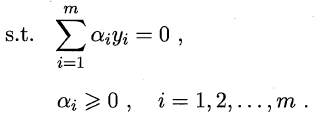
直接计算Φ(xi)TΦ(xj)通常比较困难，为此，引入”核函数“（kernel function）k(•,•)。设k(xi, xj) = <Φ(xi), Φ(xj)> = Φ(xi)TΦ(xj)，则对偶问题可以重写为
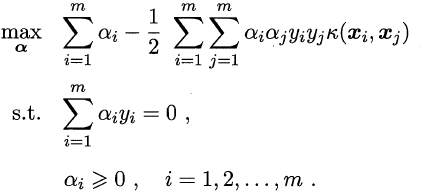
求解后即得到
此展式亦称为”支持向量展式“（support vector expansion）。
那么，合适的核函数是否一定存在？什么样的核函数能作为核函数呢？对此，有如下定理：
定理 令
为输入空间，k(•,•)为定义在
上的对称函数，则k是核函数当且仅当对于任意数据D = {x1,x2,...,xm}，”核矩阵“（kernel matrix）K总是半正定的：
书中给出了几种常见的核函数，见于下表
此外，核函数还可以通过函数组合得到：
- 若k1和k2是核函数，则k1(x,z)k2(x,z)也是核函数；
- 若k1是核函数，则对于任意函数g(x)，k(x,z) = g(x)k1(x,z)g(z)也是核函数。
二、线性支持向量机
2.1 软间隔与正则化
如前文提到的，而“软间隔”允许某些样本不满足。尽管如此，还是希望不满足约束的样本尽可能少。于是，优化目标可以改写为
其中，C>0是常数，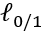
是“0/1损失函数”
为了使得优化目标更易于求解，引入一些数学性质更好的函数来替代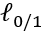，成为“替代损失”（surrogate loss）。替代损失函数通常是凸的、连续的，且是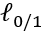的上界。下面列出了一些常用的替代损失函数：
- hinge损失：
- 指数损失(exponential loss）：
- 对率损失（logistic loss）：
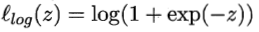
例如，如果采用hinge损失，则优化目标变为
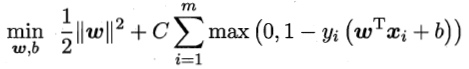
进而引入“松弛变量”（slcak variable）ξi≥0。每个样本都对应一个松弛变量，用以表征该样本不满足约束的程度。由此，上式可以重写为
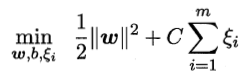
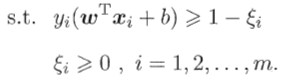
此即为常见的“软间隔支持向量机”，亦即“线性支持向量机”。
类似线性可分支持向量机的求解，首先通过lagrange乘子法得到lagrange函数
其中
，
是lagrange乘子。对ω,b,ξi分别求偏导为零，得到
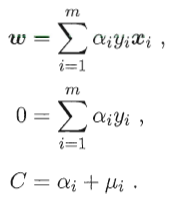
代入原式即得到对偶问题
且上述过程满足KKT条件
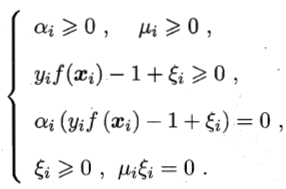
值得注意的是，SVM与对率回归的优化目标相近。比如，若将对率损失作为替代损失函数带入，则几乎就得到对率回归模型。
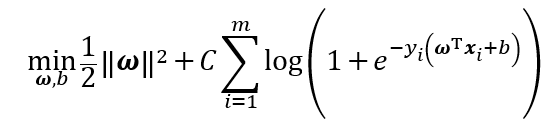
不过，与对率回归模型不同的是，SVM不具有概率意义。对率回归可直接用于多分类任务，而SVM则需要推广。另一方面，由于hinge损失有一块“平坦的”零区域，使得SVM的解具有稀疏性，而对率回归的解则依赖更多的训练样本，预测开销更大。
用不同函数作为替代损失函数得到的学习模型的性质与替代函数直接相关，但这些模型具有一个共性：即优化目标中，第一项用来描述划分超平面的“间隔”大小，另一项则用来表述训练集上的误差。于是，更一般的形式可写为
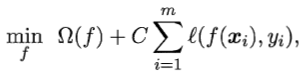
其中Ω(ƒ)称为“结构风险”（structural risk），用于描述模型自身的一些性质；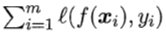
成为“经验风险”（empirical risk），用于描述与训练集的契合程度。上述形式也可称为“正则化”（regularization）问题，其中Ω(ƒ)为正则化项，C为正则化常数，而Lp范数（norm）为常用的正则化项。比如，L2范数倾向于非零分量个数尽量稠密；而L0和L1范数倾向非零分量个数尽量少。
2.2 支持向量回归
首先回顾一下回归问题：给定训练样本D = {(x1,y1), (x2,y2), ..., (xm,ym)}，希望学得一个形如的模型，使得ƒ(x)与y尽可能接近，ω和b是待确定的模型参数。基于ƒ(x)与y的差别计算损失，当且仅当ƒ(x)与y完全相同时，损失才为0。
与传统回归模型不同，“支持向量回归”（Support Vector Regression, SVR）假设我们能容忍ƒ(x)与y之间最多有ε的偏差。于是，SVR问题可以形式化为
C为正则化常数，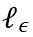
为ε-不敏感损失（ε-insensitive loss）函数
再引入松弛变量
和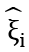
，将优化目标重写为
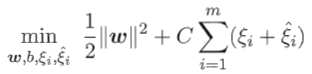
同样地，用lagrange乘子法，可以得到lagrange函数
偏导置零求解得到对偶问题
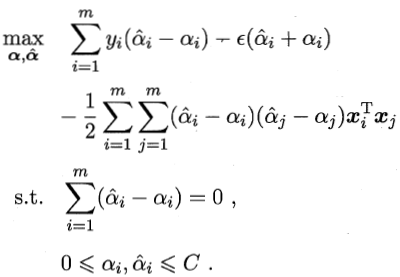SVR的解形如
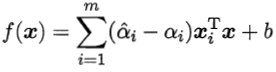
以及相应的KKT条件
其中，满足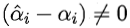
的样本即为SVR的支持向量。同样地，选取多个满足0<αi<C的样本求平均值解得b。
考虑特征映射，则利用核函数k(xi,xj)=Φ(xi)TΦ(xj)，SVR表示为
2.3 核方法
从SVM和SVR的解的形式不难看出，若不考虑偏移项b，则其学习得到的模型总能表示成核函数k(x,xi)的线性组合。事实上，对核函数，有下述“表示定理”（representer theorem）：
表示定理 令
为核函数k对应的再生希尔伯特空间，
表示
和任意非负损失函数
:
→[0,∞)，优化问题
的解总可以写为
所谓“核方法”（kernel methods），就是人们发展出的一系列基于核函数的学习方法。其中最常见的，就是通过引用核函数——“核化”——来将线性学习器拓展为非线性学习器。
下面以线性判别分析为例，介绍由核方法得到的分线性拓展，“核线性判别分析”（Kernelized Linear Discriminant Analysis, KLDA）。
设映射
将样本映射到特征空间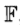
。线性判别分析在
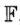中执行，以求得
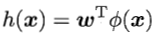。类似于在前一篇博文『机器学习中的线性模型』提到的，最大化目标为
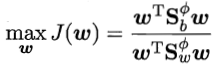
令Xi表示第i(i=0,1)类样本的集合，其样本数为mi；总样本数m=m0+m1。则第i类样本在特征空间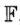中的均值为
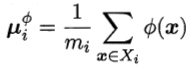
于是，类间散度矩阵和类内散度矩阵的计算公式如下
将J(ω)作为损失函数
，再令Ω≡0，由表示定理，h(x)可写为
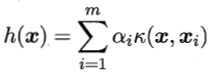
于是
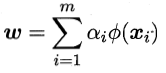
令K为核函数k对应的核矩阵，1i为第i类样本的指示向量（即1i的第j个分量为1当且仅当xj属于Xi，否则为0）。再令
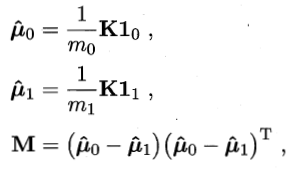
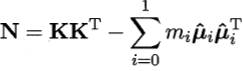
于是，KLDA的优化目标即等价为
这样以来，即便映射Φ的具体形式难以知道，只要使用线性判别分析即可求解得到α，进而可以由h(x)的表示定理表达式得到投影函数h(x)。
