1.1 基本术语
数据集(data set):数据记录的集合
示例/样本(sample):每条记录,即对一个事件/对象的描述
属性(attribute)/特征(feature):反映时间或对象在某方面的表现或性质的事项
属性空间(attribute space)/样本空间(sample space)/输入空间:属性张成的空间
由于样本空间中每一点对应于一个坐标向量,因此一个示例也成为一个特征向量(feature vector)
学习(learning)/训练(training):从数据中学习模型的过程
训练数据(training data):训练过程中使用的数据
训练集(training set):训练样本组成的集合
假设(hypothesis):学得的关于数据的某种潜在规律
真相/真实(ground-truth):关于数据的某种潜在规律自身
标记空间(label space)/输出空间:标记的集合
测试(testing):学得模型后,使用其进行预测的过程
测试样本(tesing sample):被预测的样本
根据预测的值的类型,学习任务可以被划分为分类(classification),回归(regression),聚类(clustering),etc.
根据训练数据是否有标记,学习任务可被划分为监督学习(supervised learning)与无监督学习(unsupervised learning)
泛化(generalization):学得模型适用于新样本的能力
独立同分布(independent and identically distributed, i.i.d.):样本空间中全体样本服从一个未知分布(distribution)D,获得的每个样本都是独立地从这个分布上采样获得
1.2 假设空间
可以将学习的过程看成在所有假设(hypothesis)组成的空间中进行搜索的过程,搜索目标是找到与训练集“匹配”(fit)的假设。假设的表示一旦确定,假设空间的大小就确定了。
假设空间的搜索策略:自顶向下、从一般到特殊、自底向上、从特殊到一般,etc.
现实问题中,可能有多个假设与训练集一致,即存在一个与训练集一致的“假设空间”,称之为“版本空间”(version space)。
1.3 归纳偏好
归纳偏好(inductive bias):机器学习算法在学习过程中对某种类型假设的偏好。
任何一个有效的机器学习算法必有其归纳偏好,否则它将被假设空间中看似在训练集上“等效”的假设所迷惑,而无法产生确定的学习结果。算法的归纳偏好是否与问题本身匹配,大多数时候直接决定了算法是否取得好的性能。
不存在引导算法确立正确“偏好”的一般性的原则。事实上,对于一个学习算法ζa,若它在某些问题上比学习算法ζb好,则必然存在另一些问题,使得在那里ζb比ζa好。此结论可以由如下讨论得出:
假设样本空间X和假设空间H都是离散的。令P(h|X, ζa)代表算法ζa基于训练数据X产生假设h的概率,再令f代表我们希望学习的真实目标函数。ζa的“训练集外误差”,即ζa在训练集外的所有样本上的误差为
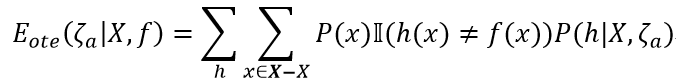
其中 是指示函数,若•为真则取1,否则取值0。
是指示函数,若•为真则取1,否则取值0。
考虑二分问题,且真实目标函数可以是任何函数X→{0,1},函数空间为{0,1}|X|。对所有可能的f,按均匀误差求和,有

上式表明,总误差与学习算法无关。对于任意两个学习算法ζa和ζb,都有

这就是NFL定理(No Free LunchTheorem, Wolpert and Macready, 1995)。当然,其前提是所有“问题”出现的几率相同,但实际情形并非如此。很多时候,我们只关注自己正在试图解决的问题。NFL的寓意,是让我们意识到,脱离具体问题,空泛谈论“什么学习算法好”毫无意义。而针对具体问题,学习算法自身的归纳偏好与问题是否匹配,往往会起决定性作用。



