算法分析基础——递归树求解递推方程

从求解快速排序算法递推方程的过程中，我们可以看到，递推方程不能求出精确的解。即便如此，如果可以用某种方法估算出函数的阶，那么这对于算法分析的工作依然具有意义。本文即介绍了这样一种估算方法，称为递归树。

递归树是一棵结点带权的二叉树。它是迭代计算的一种模型，也是其图形表示。其生成过程与迭代过程是一致的，且树上所有项恰好是迭代之后产生的和式的项。因此，对递归树上的项求和就是迭代后方程的解。运用递归树来估算递推方程的解，可以使求解过程简洁、清晰。下面我们来具体了解递归树的生成规则，并通过几项例子理解递归树的运用。

一、递归树的生成

---

 

递归树的生成规则如下：

1. 初始时，只有根节点，权标记为W(n)
2. 不断进行如下迭代：将函数项叶结点的迭代式W(m)表示成二层子树（如图1），用该子树替换叶结点。
3. 继续递归树的生成，直到树中没有函数项（树叶都变为W(1)）为止。

 

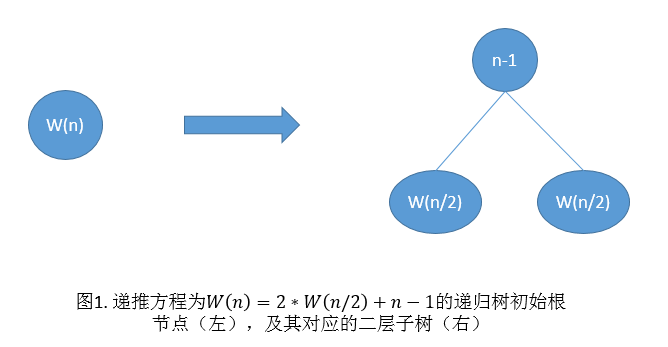
从递归树的生成过程不难看出，整个迭代过程中，递归树中全部结点的权之和不变，总是等于W(n)。为计算最终所有结点权值之和，可以采用分层计算的方法。

二、递归树的计算

---

 

例 求解递推方程T(n) = T(n/3) + T(2n/3) + n

在这项例子中，方程右部的两项不一样，无法合并。使用迭代法归纳求解不是很方便，而用递归树的方法则更加直观。

首先生成递归树如图2所示。

设树的层数为k，则n * (2 / 3)^k = 1，解得k = log_3/2n。另一方面，每层结点的数值之和都是O(n)，因此T(n) = O(nlog_3/2n) = O(nlogn)。