在分析算法时,常用的几类函数主要包括对数函数、指数函数、阶乘函数、取整函数。下文总结了一下这几类函数的阶的性质。
一、对数函数
性质1. log2N = Θ(logN)
证明 用换底公式即得证。
这一性质解释了为何,对于指数函数而言,在分析阶的关系时,可以不去考虑底数。
性质2. logbN = ο(Nα), α > 0
证明 由ln(n) = ο(nα),再结合性质1,即得证。
性质3. alogbn = nlogba
证明 由 (logbn)(logba) = (logba)(logbn),再取b的指数,即得证。
二、指数函数与阶乘
(Sirling公式)
由这一公式,可以得到以下关系:
性质1. n! = ο(nn)
性质2. n! = ω(2n)
另外,对于阶乘函数取对数,我们还有下述性质:
性质3. log(n!) = Θ(nlogn)
证明 由
知 log(n!) = Ω(nlogn)。另一方面,由
知 log(n!) = O(nlogn)。
综上可知,log(n!) = Θ(nlogn)。证毕。
三、取整函数
取整函数的主要性质如下:
性质1. x - 1 < floor(x) ≤ x ≤ ceil(x) < x + 1
性质2. ceil(x + n) = ceil(x) + n, n为正整数
性质3. ceil(ceil(n / a) / b) = ceil(n / (ab)), floor(floor(n / a) / b) = floor(n / (ab)).
证明过程是简单的,此处就省略了。值得注意的是,在二分查找与归并排序是,取的轴值皆是由向下取整函数得到。

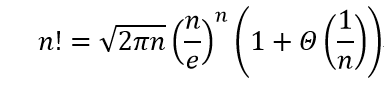
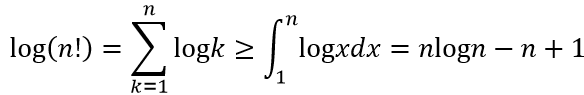
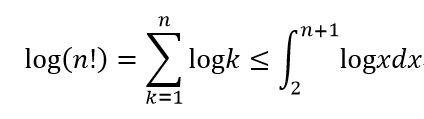

 浙公网安备 33010602011771号
浙公网安备 33010602011771号