POJ1569 Myacm Triangles

Description

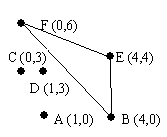
There has been considerable archeological work on the ancient Myacm culture. Many artifacts have been found in what have been called power fields: a fairly small area, less than 100 meters square where there are from four to fifteen tall monuments with crystals on top. Such an area is mapped out above. Most of the artifacts discovered have come from inside a triangular area between just three of the monuments, now called the power triangle. After considerable analysis archeologists agree how this triangle is selected from all the triangles with three monuments as vertices: it is the triangle with the largest possible area that does not contain any other monuments inside the triangle or on an edge of the triangle. Each field contains only one such triangle. 

Archeological teams are continuing to find more power fields. They would like to automate the task of locating the power triangles in power fields. Write a program that takes the positions of the monuments in any number of power fields as input and determines the power triangle for each power field. 

A useful formula: the area of a triangle with vertices (x1, y1), (x2, y2), and (x3, y3) is the absolute value of 

0.5 * [(y3 - y1)(x2 - x1) - (y2 - y1)(x3 - x1)]. 

Input

For each power field there are several lines of data. The first line is the number of monuments: at least 4, and at most 15. For each monument there is a data line that starts with a one character label for the monument and is followed by the coordinates of the monument, which are nonnegative integers less than 100. The first label is A, and the next is B, and so on. 

There is at least one such power field described. The end of input is indicated by a 0 for the number of monuments. The first sample data below corresponds to the diagram in the problem.

Output

For each power field there is one line of output. It contains the three labels of the vertices of the power triangle, listed in increasing alphabetical order, with no spaces.

Sample Input

6
A 1 0
B 4 0
C 0 3
D 1 3
E 4 4
F 0 6
4
A 0 0
B 1 0
C 99 0
D 99 99
0

Sample Output

BEF
BCD

『题解』

题目大意是给一些点，这些点可以构成很多三角形。要在所有内部不含其它点的三角形中找出面积最大的。

枚举三角形的三个顶点a，b，c。主要问题在于如何判断三角形内没有其它的点。事实上，若点p在三角形abc内，则叉积(a - b) ^ (p - b)，(b - c) ^ (p - c)，(c - a) ^ (p - a)是同号的。此方法同样适用与判断点是否在凸多边形内。

三角形abc面积的求法题目给出了，用叉积|(a - b) ^ (c - b) / 2|。在满足条件的三角形中找面积最大的即可。

枚举三角形的三个顶点，对于每个三角形还要枚举判断内部是否包含其它点，因而时间复杂度为O(n ^ 4)。

 

『C++』

#include <iostream>
#include <cmath>
#include <algorithm>
#include <stdlib.h>
using namespace std;

struct Vector {
    double x, y;
    Vector() :x(0), y(0) {}
    Vector(double xx, double yy) :
        x(xx), y(yy) {}
}pts[50];

int n;

double operator ^(const Vector &v1, const Vector &v2) {
    return v1.x * v2.y - v1.y * v2.x;
}

Vector operator -(const Vector &v1, const Vector &v2) {
    return Vector(v1.x - v2.x, v1.y - v2.y);
}

double Area(const Vector &A, const Vector &B, const Vector &C) {
    return fabs(0.5 * ((B - A) ^ (C - A)));
}

bool InTriangle(const Vector &A, const Vector &B, 
    const Vector &C, const Vector &P) {
    double d1 = (A - B) ^ (P - B);
    double d2 = (B - C) ^ (P - C);
    double d3 = (C - A) ^ (P - A);

    if ((d1 >= 0 && d2 >= 0 && d3 >= 0) ||
        (d1 <= 0 && d2 <= 0 && d3 <= 0))
        return true;
    return false;
}

bool Check(int pn1, int pn2, int pn3) {
    for (int i = 0; i < n; i++) {
        if (i == pn1 || i == pn2 || i == pn3)
            continue;
        if (InTriangle(pts[pn1], pts[pn2], pts[pn3], pts[i]))
            return false;
    }
    return true;
}

int main()
{
    while (scanf_s("%d", &n) == 1 && n) {
        if (n == 0)break;

        double ans = 0;
        int num[3] = {};

        for (int i = 0; i < n; i++) {
            char c;
            cin >> c >> pts[i].x >> pts[i].y;
        }

        for(int i = 0; i < n; i++)
            for(int j = i + 1; j < n; j++)
                for(int k = j+1; k < n; k++)
                    if (Check(i, j, k)) {
                        double area = Area(pts[i], pts[j], pts[k]);
                        if (ans < area) {
                            ans = area;
                            num[0] = i;
                            num[1] = j;
                            num[2] = k;
                        }
                    }

        printf("%c%c%c\n", 'A' + num[0], 'A' + num[1], 'A' + num[2]);
    }

    //system("pause");
    return 0;
}