第六章小结--图
想了很多,打算决定每天都在这个上面加一点自己当天学到的,还有自己思考的东西,一点一点加,或许会更有效率,也会记录我的思考过程吧。
5.12
今天做了PTA上的选择题
1、用一维数组G[]存储有4个顶点的无向图如下:
G[] = { 0, 1, 0, 1, 1, 0, 0, 0, 1, 0 }
推出:则顶点2和顶点0之间是有边的。
2、如果用邻接表存储结构,在对图进行广度优先遍历时一般要用到的一种数据结构类型是--队列
3、给定有权无向图的邻接矩阵如下,其最小生成树的总权重是:8

4、如果G是一个有15条边的非连通无向图,那么该图顶点个数最少7---n(n-1)*1/2 + 1
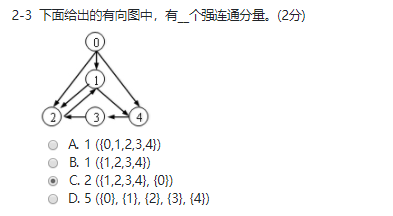
图的遍历:
深度优先
类似于树的先序遍历
直到刚访问的顶点没有未被访问的顶点为止。
算法实现(遍历连通图):

1 bool visited[MVNum]; //访问标志数组,其初值为“false” 2 void DFS(Graph G, int v) 3 {//从第v个顶点出发递归地深度优先遍历图G 4 cout<<v; visited[v] = ture; 5 for(w=FirstAdjVex(G,v);w>=0;w=NexAdjVex(G,v,x)) 6 //依次检查v的所有邻接点,First...表示v的第一个邻接点 7 //Nex...表示v相对于w的下一个邻接点,w>=0表示存在邻接点 8 if(!visited[w]) DFS(G,w); 9 10 }
(非连通图)

void DFSTraverse(Graph G) {//对非连通图G做深度优先遍历 for(v=0;v<G.vexnum;++v) visited[v]=false;//访问标志数组初始化 for(v=0;v<G.Vexnum;++v) //循环调用遍历连通图算法 if(!visited[v]) DFS(G,v); //对尚未访问的顶点调用DFS }
(邻接矩阵)

1 void DFS_AM (AMGraph G,int v) 2 {//图G为邻接矩阵类型,从第v个顶点出发深度优先搜索遍历图G 3 cout<<v; visited[v]=true;//访问第v个顶点,并置访问的标志数组相应的分量值为true 4 for(w=0;w<G.vexnum;w++)//依次检查邻接矩阵v所在的行 5 if((G.arcs[v][w]!=0)&&(!visited[w])) DFS_AM(G,w);//G.arcs[v][w]表示w是v的邻接点,如果w未访问,则递归调用DFS_AM 6 7 8 }
(邻接表)
广度优先
广度优先遍历其实类似于一个队列,但是分两种(我已知):
1.先访问,再入队;
if(未访问)
出队元素的每一个邻接点先访问再入队
2.直接入队;
if(未访问) 访问,该点的所有邻接点入队
最小生成树:
给定一个无向图,如果它任意两个顶点都联通并且是一棵树,那么我们就称之为生成树(Spanning Tree)。
在一个连通网的所有生成树中,各边的代价之和最小的那棵生成树称为该联通网的最小代价生成树,(如果是带权值的无向图,那么权值之和最小的生成树)我们就称之为最小生成树(MST, Minimum Spanning Tree)。
常见求解最小生成树的算法有Kruskal算法和Prim算法
Prim算法
选定一个顶点后一次根据边的权值对点进行连接,与Kruskal算法类似,但不同之处在于,P为“加点法”,K为“加边法”
Kruskal算法
建议还是画图的话,容易解决一点,相对于分成两个集合,一个是V集合,一个是U-V集合,同时还有需要进行读入+刷新
本周回顾:
由于上周特别忙碌,以及对树的代码的背诵没有完成很好,于是对自己的emmm信心又失去了。虽然对一些代码的知识有了些了解,比如完成书上的课后习题,但是还是有很多的问题需要改进,如今到了图,真心开始害怕,倒不是说对分析怎么样,但是对于打代码开始方了,分析较打代码要好很多,原因是只需要在需求的层面上去根据逻辑,并不需要敲代码来实现。反正现在已经有了恐惧心理了。
新的目标:
完成本周作业,同时能够把树的代码重新搞懂,理顺之前的作业吧。
本周作业还没有整理出来,虽然是要逼出来的,但是有的时候钻到牛角尖里面去,只有可能适得其反好吧。有的话就不多说,就这样吧。反正是不可能自闭的,就是放弃差不多吧。
第一道作业题的博客:
https://www.cnblogs.com/JeffKing11/p/10923481.html
第二道作业题的博客:
还在更新...



