基于GPU屏幕空间的精确光学折射效果
摘要:在实时渲染中,光学物体的折射效果极大的影响场景的真实特性。由于GPU是以光栅化而不是光线跟踪的方式工作的,精确的进行光学特性的模拟需要极大的计算量。Chris Wyman展示了一种简单的基于屏幕空间的折射效果的实现,得到的效果已经极大的接近光线跟踪的结果。而且他的这种方法在最新的由Technische Universität München慕尼黑工业大学在GPGPU.ORG上展示的《Interactive Screen-Space Accurate Photon Tracing on GPUs》这篇文章中都有所提及。这篇我只是简单的实现了Wyman的方法,详情大家可以去Google搜索《An Approximate Image-Space Approach for Interactive Refraction》这篇文章。
在Cg、HLSL、GLSL中都有Refract与Reflect这两个函数。Reflect大部分用于环境贴图坐标的计算,Refract用于表现一个透明物体的光线折射特性。事实上,当我们在启用了深度测试的屏幕上计算的折射效果时,已经暗示了透明物体只有一层,也就是说我们计算的折射向量是完全错误的,因为折射光线还需要与后面,经过深度缓冲已经剔除的后面发生第二次折射,这样第二次计算过折射向量后才能够作为纹理坐标查询环境贴图。图示如下:
Wyman使用的方法很简单。运用Multipass多通道技术,分别使用两种深度测试,以物体的向量作为顶点颜色,分别输出4张纹理。渲染时只需要3张。分别如下:
这是“前面”,使用glClearDepth(1)与glDepthFunc(GL_LESS)这两个参数进行深度测试的结果。相应的深度贴图如下:
还有“后面”,使用glClearDepth(0)与glDepthFunc(GL_GREATER)进行测试。
相应的深度纹理。
我们可以通过FragmentShader,把两张深度纹理相减,获得Perspective方式下的物体前后面的距离d(PS:光线跟踪就没有这样简便了,需要多次遍历测试三角形)。注意,这是在Perspective方式下的距离,不是精确的几何距离,后面我们将看到如何看待这个问题。
对于需要进行折射计算的物体,我们可以很方便的在VertexShader中得到下面的信息:
每个顶点的位置P1
相应顶点的向量N1
从视点到顶点的向量V
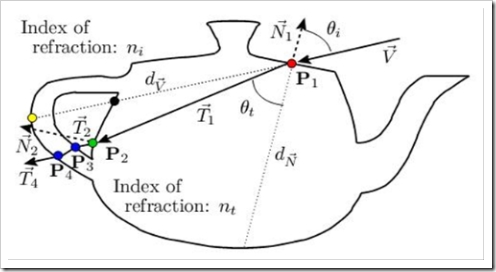
从文章开头的示意图中可以知道,“后面”的点P2 = P1 + dT1。而且只要我们知道了P2和N2就可以得到了准确的第二次折射的结果。不过我们考虑一个实时,就是当折射体的折射率过大时,折射光线将非常靠近-N1。Wyman对比了其他人的方法,建议对d进行插值计算:
Hoppe(此人是微软DirectX开发组的专家,D3D中的那个优化Mesh功能就是他博士论文的直接成果)使用预计算的Geometry Image进行采样,不过会产生不连续的d导致走样。这个d的计算非常的蹊跷,让我们先看下Wyman的伪代码。
 for all fragments F (given P1 , V, and N1 ), do
for all fragments F (given P1 , V, and N1 ), do 
 T1 = Refract( V, N1 )
T1 = Refract( V, N1 ) 
 dV1 = DistanceFrontFaceToBackFace( F, BackfaceZBuf )
dV1 = DistanceFrontFaceToBackFace( F, BackfaceZBuf ) 
 dN = DistanceAlongNormal( P1 )
dN = DistanceAlongNormal( P1 ) 
 d =WeightDistance( - N1 ·T1 , V1 ·T1 , dV1 , dN )
d =WeightDistance( - N1 ·T1 , V1 ·T1 , dV1 , dN ) 
 P2 = P1 + dT1
P2 = P1 + dT1 
 texFar = ProjectToScreenSpace( P2 )
texFar = ProjectToScreenSpace( P2 ) 
 N2 ≈ TextureLookup( texFar , BackfaceNormals )
N2 ≈ TextureLookup( texFar , BackfaceNormals ) 
 T2 ≈ Refract( T1 , N2 )
T2 ≈ Refract( T1 , N2 ) 
 return IndexEnvironmentMap( T2 )
return IndexEnvironmentMap( T2 ) 
有了第一次折射的光线T1后,我们需要找到P2以获得那个面上的N2,以用来再次计算出射向量。而P2又是和d密切相关的,我们如何获得这个d,也就是法线方向上的垂直距离呢?
对于茶壶,球体、立方体等等这些规则的物体,我们可以简单的使用立体几何的知识进行计算。比如图1的那个d,假如我们已经知道茶壶的半径,那么我们可以简单的利用Object Coordinates计算,d 近似等于sqrt(y^2 + R^2)。即使是不规则的物体,只要我们知道它的主要入射方向上所有的顶点,我们就可以预先计算好插值过的d。
下面是使用单次折射与多次折射两种效果的对比:
可以看出多次折射在Teapot体上显示出了更多的效果,多了一个小斑点呵呵。
第二通道相应的Vertex Shader的代码如下:

2
 varying vec4 ProjTexCoord;
varying vec4 ProjTexCoord;3
 varying vec3 EyeDir;
varying vec3 EyeDir;4
 varying vec3 RefractDir;
varying vec3 RefractDir;5
 varying vec3 Normal;
varying vec3 Normal;6
 varying float dN;
varying float dN;7

8
 void main()
void main()9
 {
{10
 gl_TexCoord[0] = gl_MultiTexCoord0;
gl_TexCoord[0] = gl_MultiTexCoord0;11
 ProjTexCoord = gl_ModelViewProjectionMatrix*gl_Vertex;
ProjTexCoord = gl_ModelViewProjectionMatrix*gl_Vertex;12
 ProjTexCoord.xy = 0.5 * (ProjTexCoord.xy + ProjTexCoord.ww ) ;
ProjTexCoord.xy = 0.5 * (ProjTexCoord.xy + ProjTexCoord.ww ) ;13
 ProjTexCoord.z = 0.5 * (ProjTexCoord.z + ProjTexCoord.w + 0.64);
ProjTexCoord.z = 0.5 * (ProjTexCoord.z + ProjTexCoord.w + 0.64);14
 ProjTexCoord.xyz *= ProjTexCoord.w;
ProjTexCoord.xyz *= ProjTexCoord.w;15

16
 EyeDir = normalize( vec3(gl_ModelViewMatrix*gl_Vertex) );
EyeDir = normalize( vec3(gl_ModelViewMatrix*gl_Vertex) );17
 Normal = normalize( gl_NormalMatrix*gl_Normal );
Normal = normalize( gl_NormalMatrix*gl_Normal );18
 RefractDir = refract(EyeDir,Normal,0.65); //the first time reflect
RefractDir = refract(EyeDir,Normal,0.65); //the first time reflect19
 dN = sqrt(pow(gl_Vertex.y,2.0)+1.0);
dN = sqrt(pow(gl_Vertex.y,2.0)+1.0);20

21
 gl_Position = ftransform();
gl_Position = ftransform();22
 }
}23

Fragment Shader
 uniform sampler2D Tex0;
uniform sampler2D Tex0;2
 uniform sampler2D Tex1;
uniform sampler2D Tex1;3
 uniform sampler2D Tex2;
uniform sampler2D Tex2;4
 uniform samplerCube Tex3;
uniform samplerCube Tex3;5

6

7
 varying vec4 ProjTexCoord;
varying vec4 ProjTexCoord;8
 varying vec3 EyeDir;
varying vec3 EyeDir;9
 varying vec3 RefractDir;
varying vec3 RefractDir;10
 varying vec3 Normal;
varying vec3 Normal;11
 varying float dN;
varying float dN;12

13
 void main()
void main()14
 {
{15

16
 float bias = 1.0/512.0;
float bias = 1.0/512.0;17
 float dV1 = texture2DProj(Tex2,ProjTexCoord.xyz).x - texture2DProj(Tex1,ProjTexCoord.xyz).x;
float dV1 = texture2DProj(Tex2,ProjTexCoord.xyz).x - texture2DProj(Tex1,ProjTexCoord.xyz).x;18
 float d = mix(dV1,dN,dot(Normal,EyeDir)/dot(Normal,RefractDir));
float d = mix(dV1,dN,dot(Normal,EyeDir)/dot(Normal,RefractDir));19
 vec3 P2 = -EyeDir + d*RefractDir;
vec3 P2 = -EyeDir + d*RefractDir;20
 vec3 N2 = texture2DProj(Tex0,P2.xyz).rgb;
vec3 N2 = texture2DProj(Tex0,P2.xyz).rgb;21
 vec3 T2 = refract(RefractDir,N2,0.65);
vec3 T2 = refract(RefractDir,N2,0.65);22
 vec3 color = textureCube(Tex3,T2).rgb;
vec3 color = textureCube(Tex3,T2).rgb;23
 gl_FragColor = vec4(color,1.0);
gl_FragColor = vec4(color,1.0);24
 }
}25

暴露出的问题
显然,这种方法只考虑的比较规则的模型,甚至连这个茶壶都无法模拟精确,只能对凸立方体有起作用,如果几何体过于复杂,它将只得到第二次折射是最终的结果,对于更加小范围的折射将忽略。而且考虑到光谱,RGB三种颜色的反射率并不同,所以对于更加精确的模拟我更倾向于使用三种颜色分别计算,合成最终的反射向量进行查询。
我觉得现有的模型表现方法无法满足实际的需求,而如果要基于物理实现更多的效果,更多物体的数值需要被预先计算得到,光栅化的操作却是比不上光线跟踪来的效果。






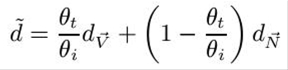





 浙公网安备 33010602011771号
浙公网安备 33010602011771号