[已完结]CMU数据库(15-445)实验2-B+树索引实现(下)
[已完结]CMU数据库(15-445)实验2-B+树索引实现(下)
4. Index_Iterator实现#
这里就是需要实现迭代器的一些操作,比如begin、end、isend等等
下面是对于IndexIterator的构造函数
其中idx表示当前page中的第几个tuple
INDEXITERATOR_TYPE::IndexIterator(LeafPage *leftmost_leaf, int idx, BufferPoolManager *buffer_pool_manager)
: curr_page(leftmost_leaf), curr_index(idx), bpm(buffer_pool_manager) {}
1. 首先我们来看begin函数的实现#
- 利用key值找到叶子结点
- 然后获取当前key值的index就是begin的位置
Page *page = FindLeafPage(KeyType{}, true); // leftmost_leaf pinned
LeafPage *leftmost_leaf = reinterpret_cast<LeafPage *>(page->GetData());
buffer_pool_manager_->UnpinPage(leftmost_leaf->GetPageId(), false);
return INDEXITERATOR_TYPE(leftmost_leaf, 0, buffer_pool_manager_);
2. end函数的实现#
- 找到最开始的结点
- 然后一直向后遍历直到
nextPageId=-1结束 - 这里注意需要重载
!=和==
end函数
// find the right most page
Page *page = FindLeafPage(KeyType{}, true); // page pinned
LeafPage *leaf = reinterpret_cast<LeafPage *>(page->GetData());
while (leaf->GetNextPageId() != INVALID_PAGE_ID) {
page_id_t next_page_id = leaf->GetNextPageId();
buffer_pool_manager_->UnpinPage(leaf->GetPageId(), false); // page unpinned
Page *next_page = buffer_pool_manager_->FetchPage(next_page_id); // next_page pinned
leaf = reinterpret_cast<LeafPage *>(next_page->GetData());
}
return INDEXITERATOR_TYPE(leaf, leaf->GetSize(), buffer_pool_manager_);
==和 !=函数
这里注意在!= 那里不能写成itr != *this
INDEX_TEMPLATE_ARGUMENTS
bool INDEXITERATOR_TYPE::operator==(const IndexIterator &itr) const {
return itr.curr_page == curr_page && itr.curr_index == curr_index;
}
INDEX_TEMPLATE_ARGUMENTS
bool INDEXITERATOR_TYPE::operator!=(const IndexIterator &itr) const { return !(itr == *this); }
3. 重载++和*(解引用符号)#
- 重载++
简单的index++然后设置nextPageId即可
INDEX_TEMPLATE_ARGUMENTS
INDEXITERATOR_TYPE &INDEXITERATOR_TYPE::operator++() {
curr_index++;
if (curr_index == curr_page->GetSize() && curr_page->GetNextPageId() != INVALID_PAGE_ID) {
page_id_t next_pid = curr_page->GetNextPageId();
Page *next_page = bpm->FetchPage(next_pid); // pined page
LeafPage *next_node = reinterpret_cast<LeafPage *>(next_page->GetData());
curr_page = next_node;
bpm->UnpinPage(next_page->GetPageId(), false);
curr_index = 0;
}
return *this;
}
- 重载*
return array[index]即可
const MappingType &INDEXITERATOR_TYPE::operator*() { return curr_page->GetItem(curr_index); }
5. 并发机制的实现#
0. 首先复习一下读写🔒机制#
- 读操作是可以多个进程之间共享latch的而写操作则必须互斥
- 加入
MaxReader数就是为了防止等待的⌛️写进程饥饿
首先来看如果没有🔒机制多线程会发生什么问题
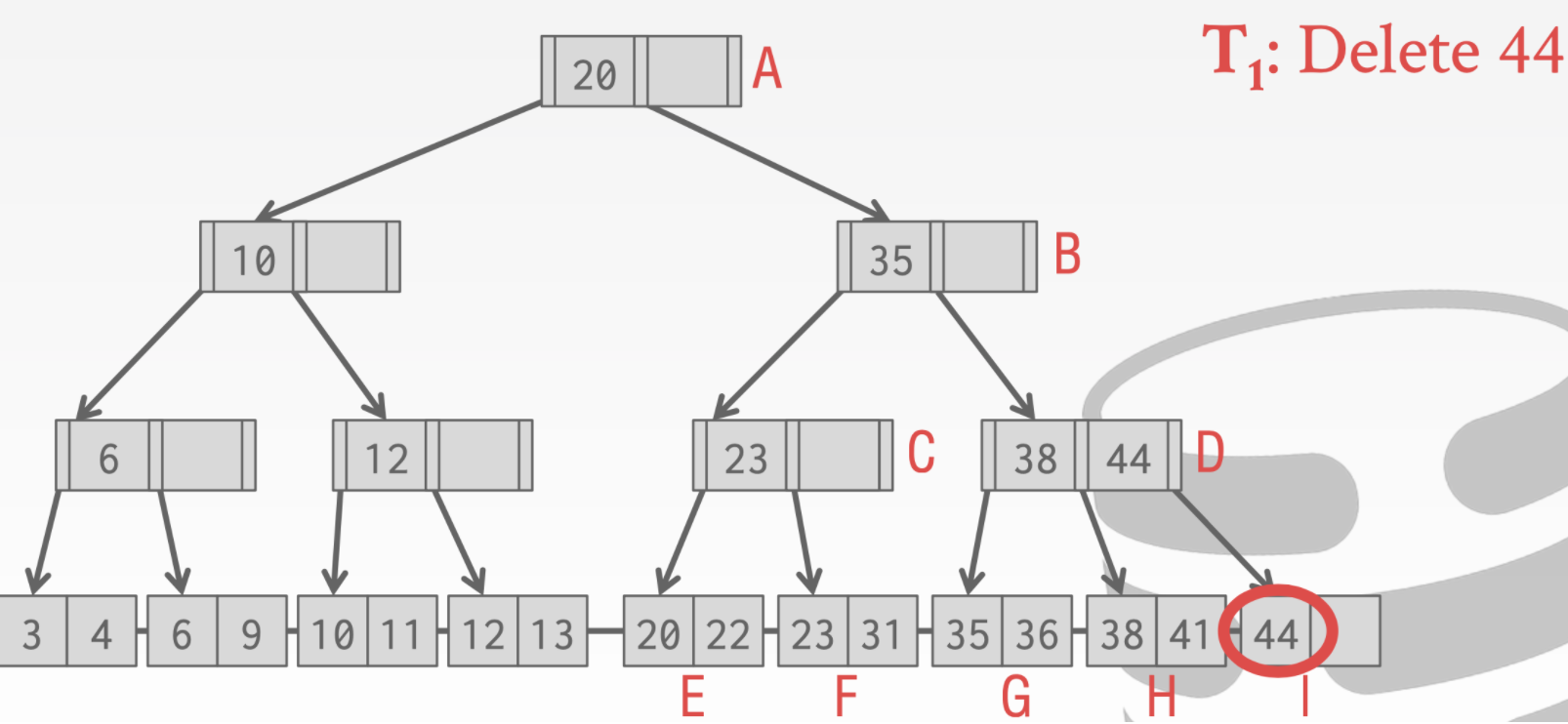
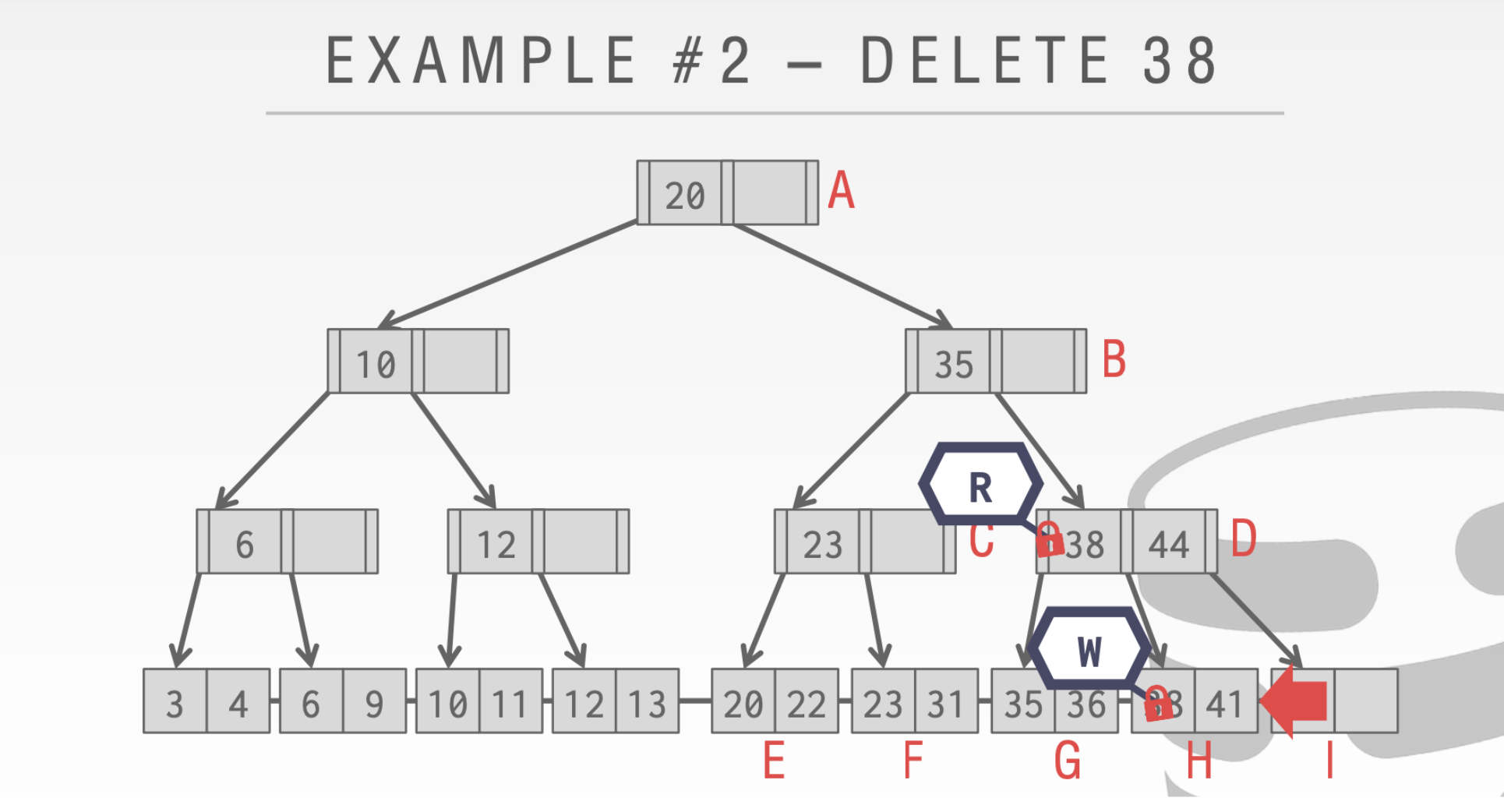
- 线程T1想要删除44。
- 线程T2 想要查找41
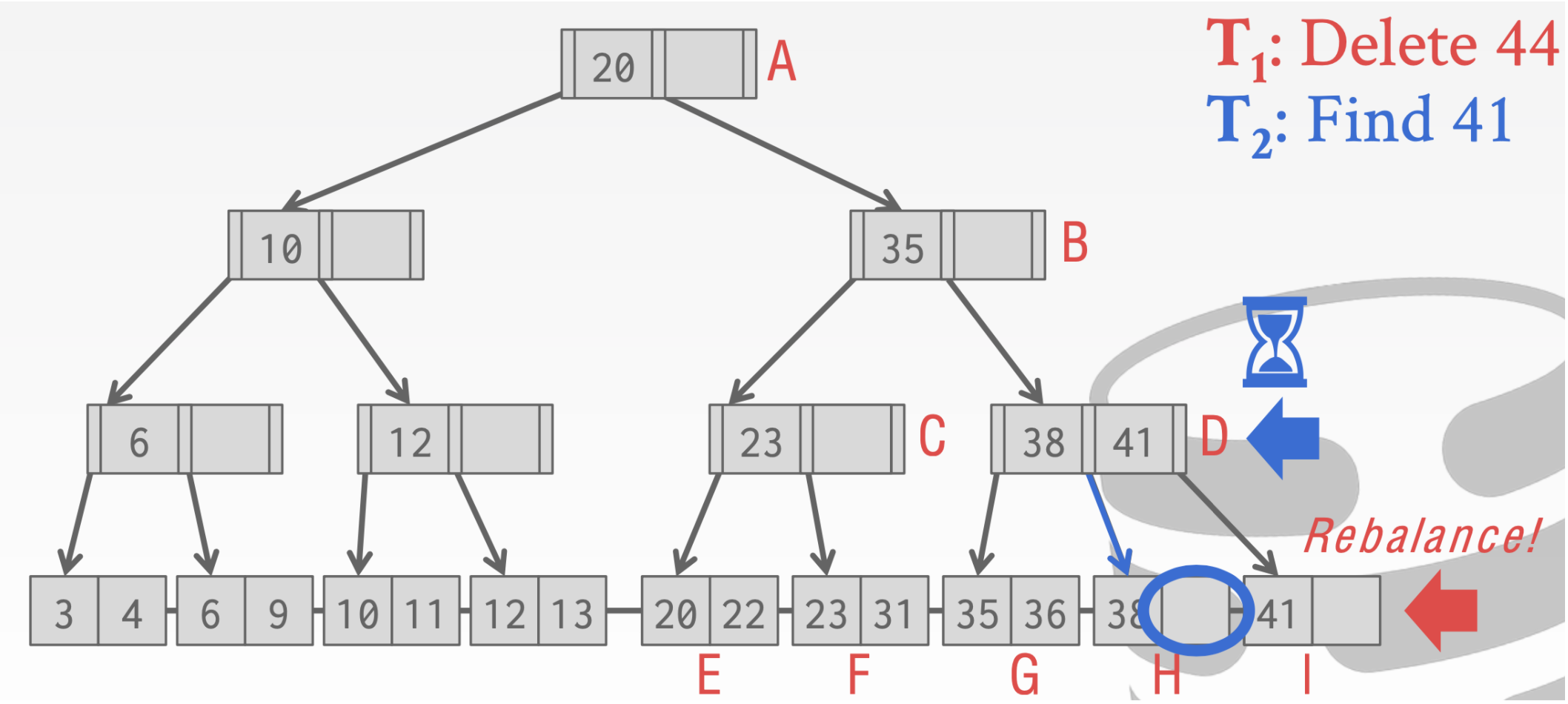
- 假设T2在执行到D位置的时候又切换到线程T1
- 这个时候T1进行重新分配,会把41借到I结点上
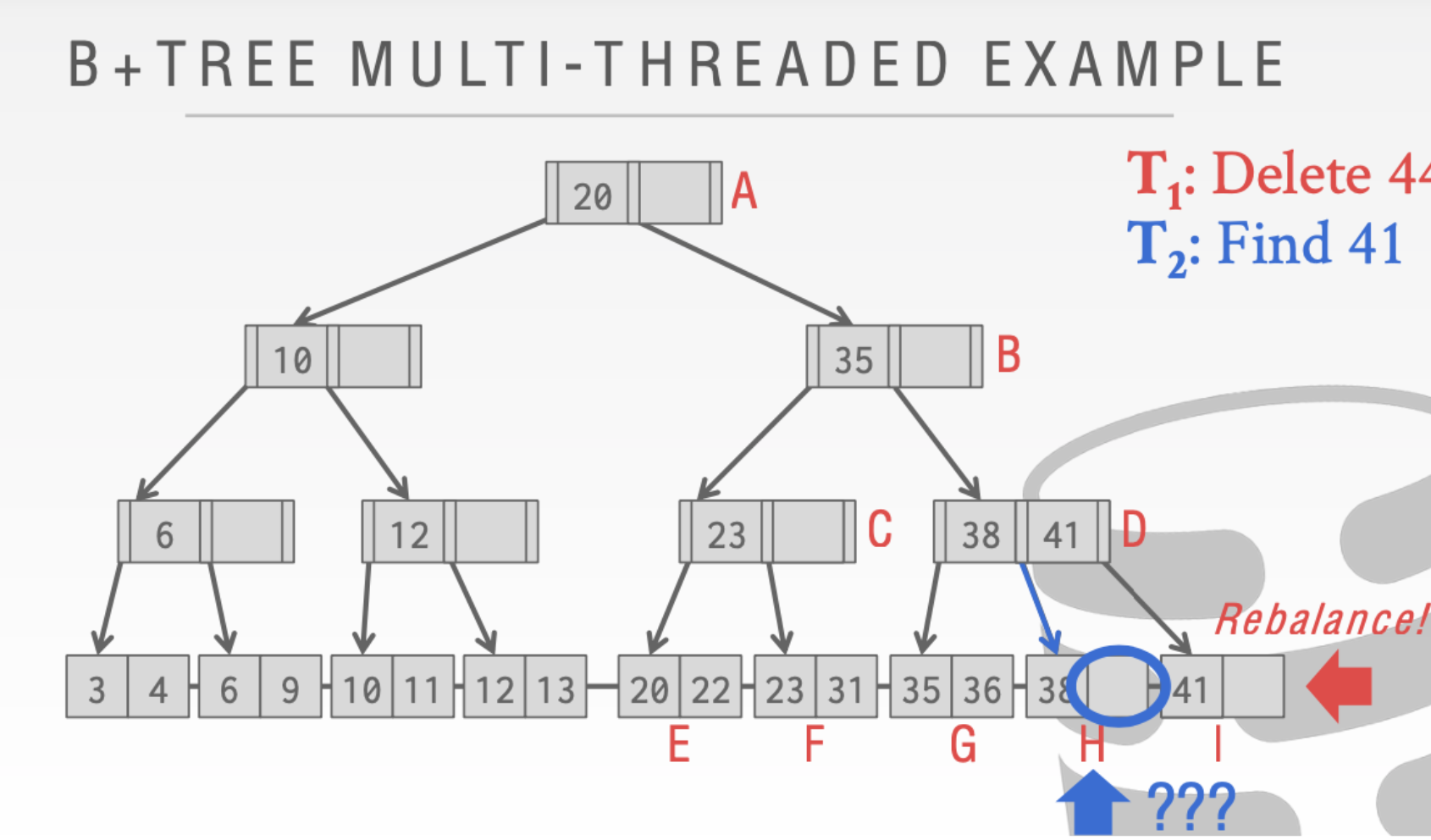
- T1执行完成切换回T2这时候T2再去原来的执行寻找41就会找不到
就会出现下面的情况。❓
由此我们需要读写🔒的存在
-
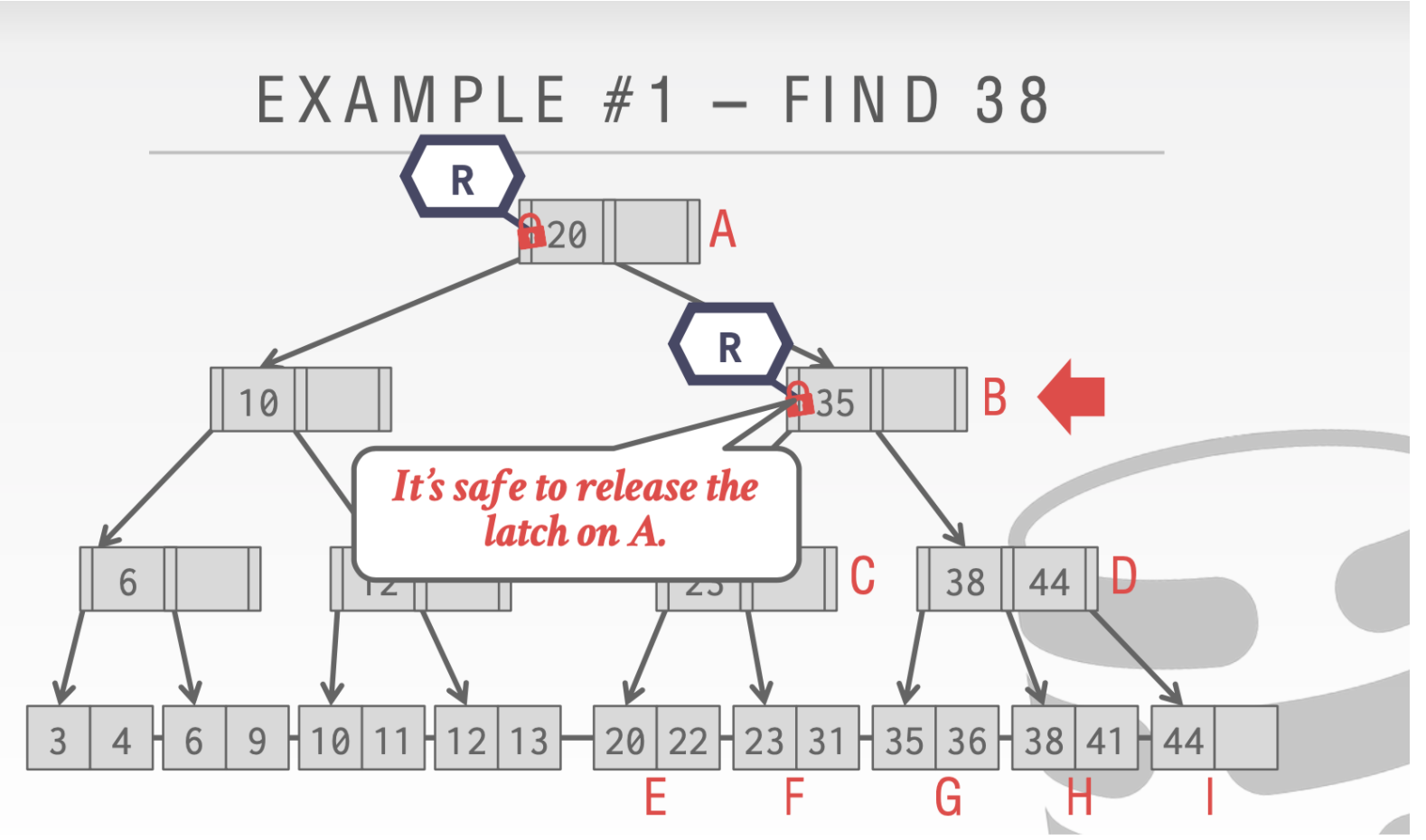
对于find操作
由于我们是只读操作,所以我们到下一个结点的时候就可以释放上一个结点的Latch
剩下的操作都是一样的
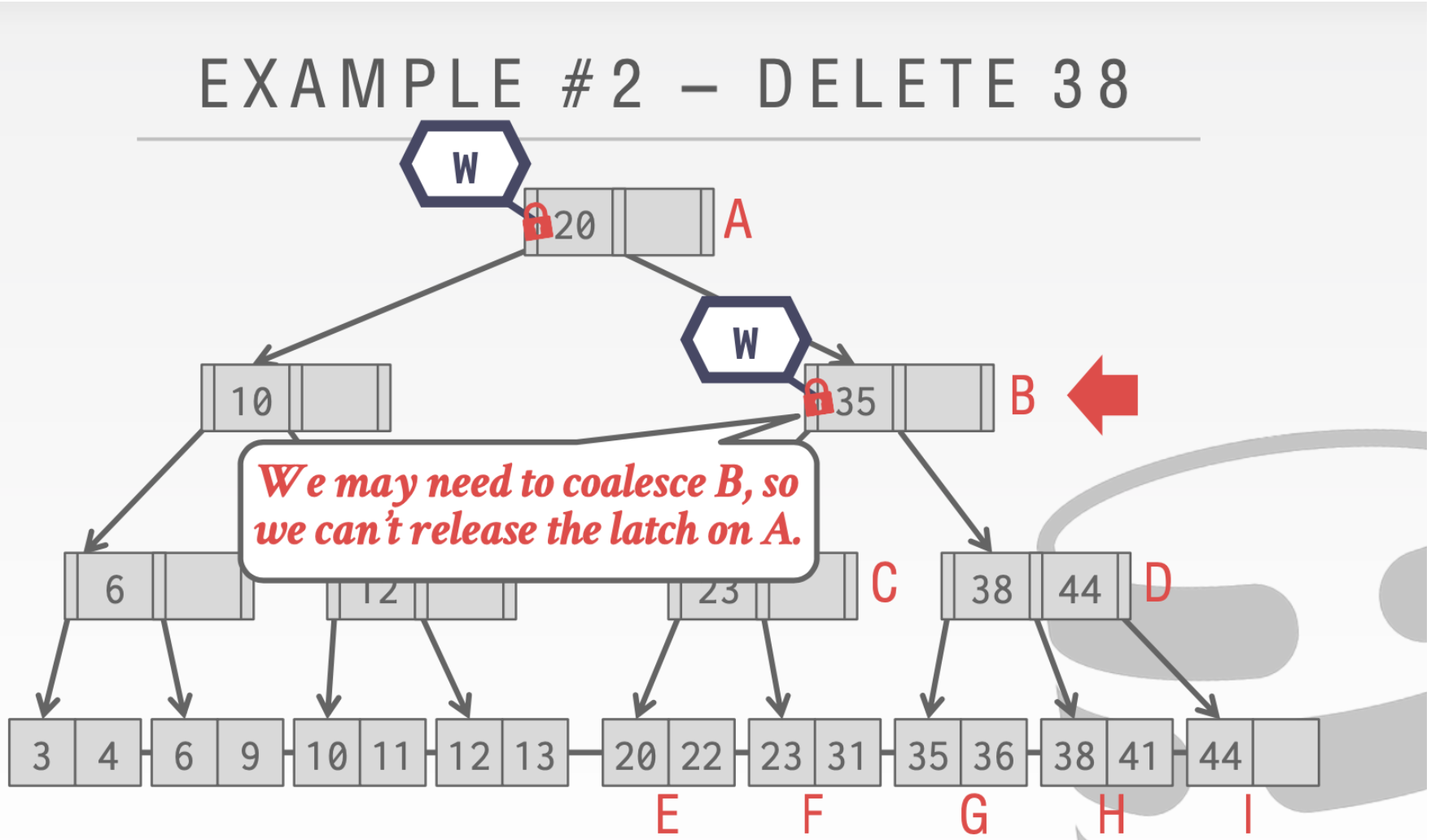
对于delete则不一样
因为我们需要写操作
这里我们不能释放结点A的Latch。因为我们的删除操作可能会合并根节点。
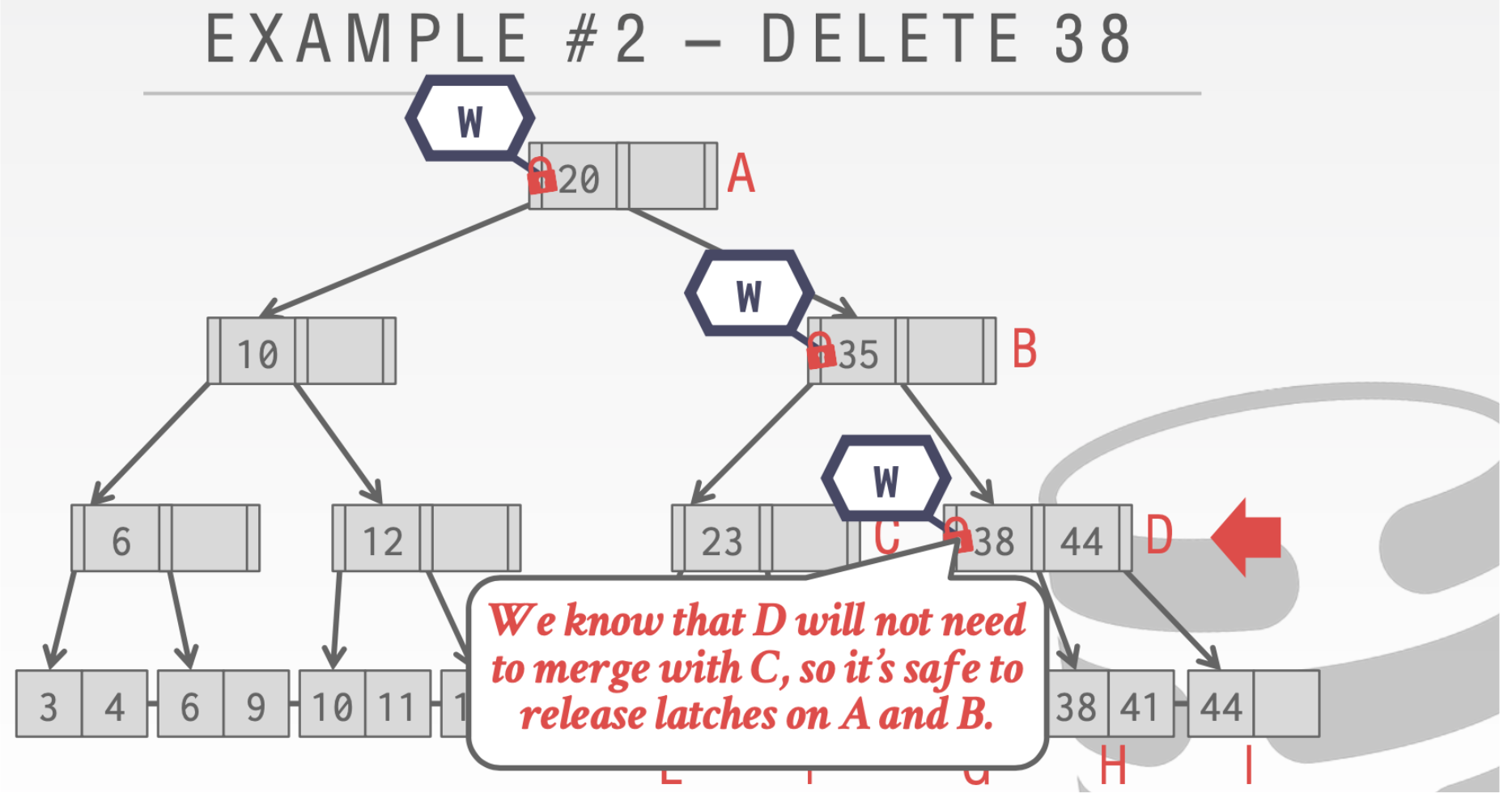
到D的时候。我们会发现D中的38删除之后不需要进行合并,所以对于A和B的写Write是可以安全释放了
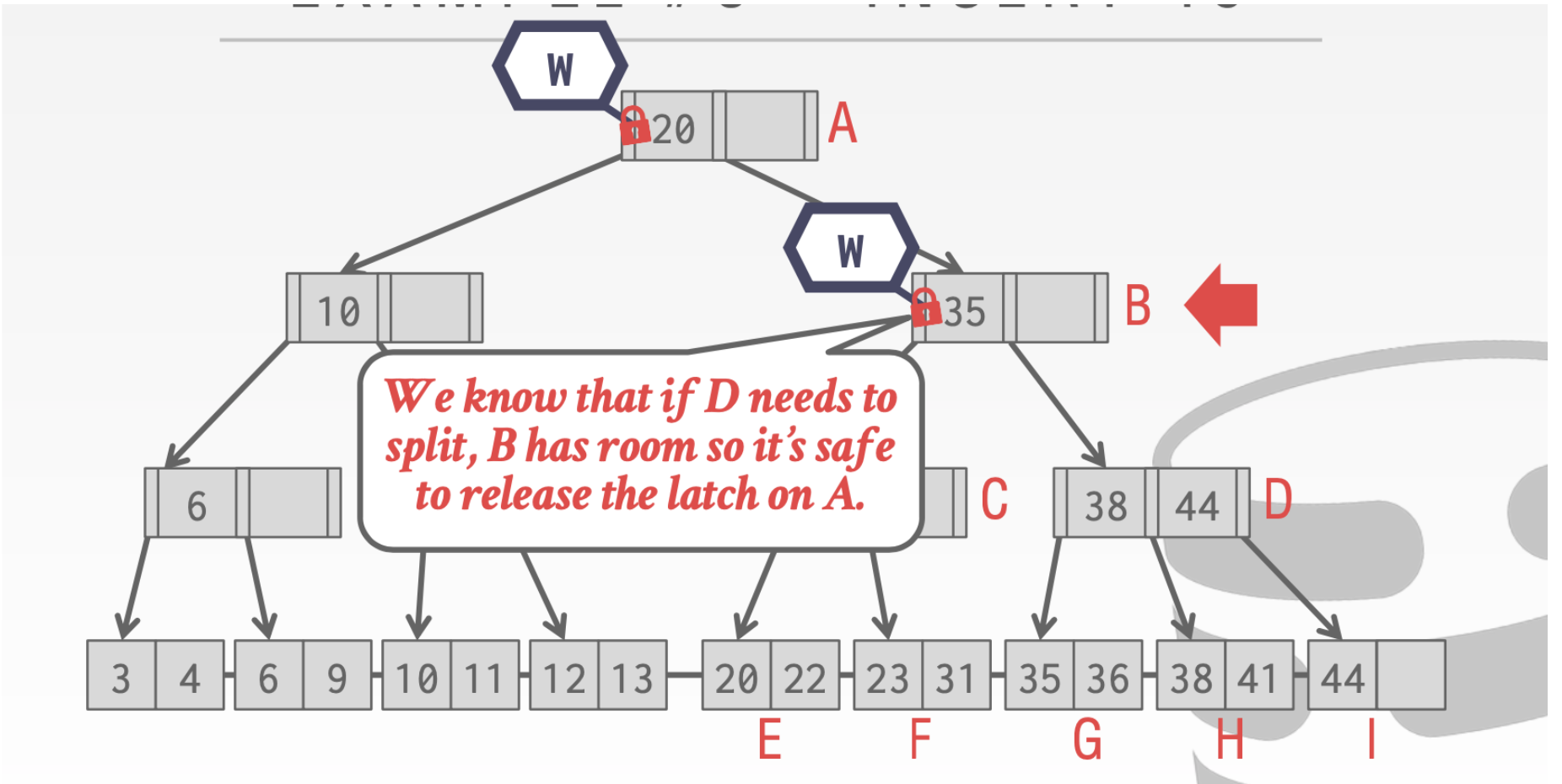
对于Insert操作
这里我们就可以安全的释放掉A的锁。因为B中还有空位,我们插入是不会对A造成影响的
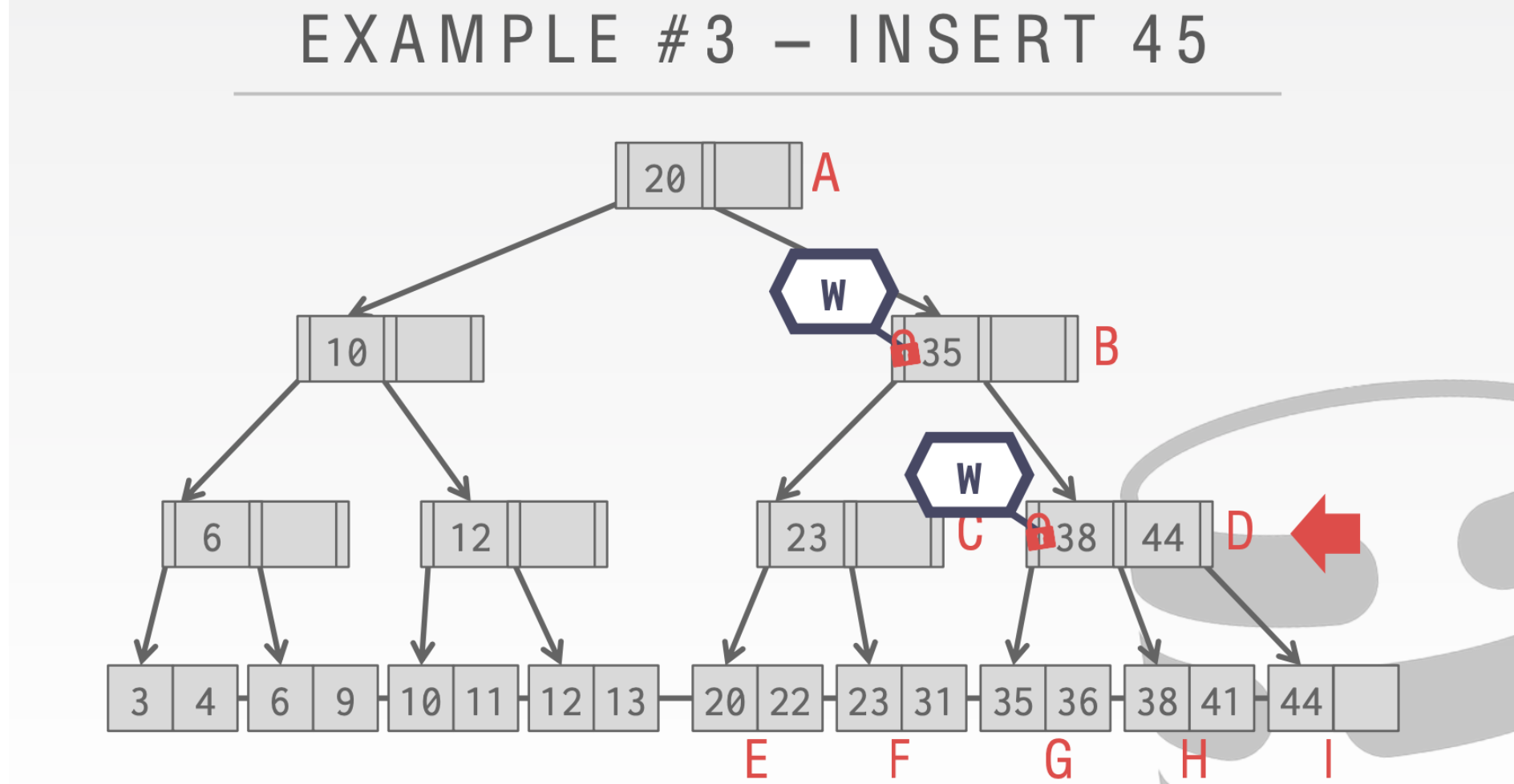
当我们执行到D这里发现D中已经满了。所以此时我们不会释放B的锁,因为我们会对B进行写操作
上面的算法虽然是正确的但是有瓶颈问题。由于只有一个线程可以获得写Latch。而插入和删除的时候都需要对头结点加写Latch。所以多线程在有许多个插入或者删除操作的时候,性能就会大打折扣
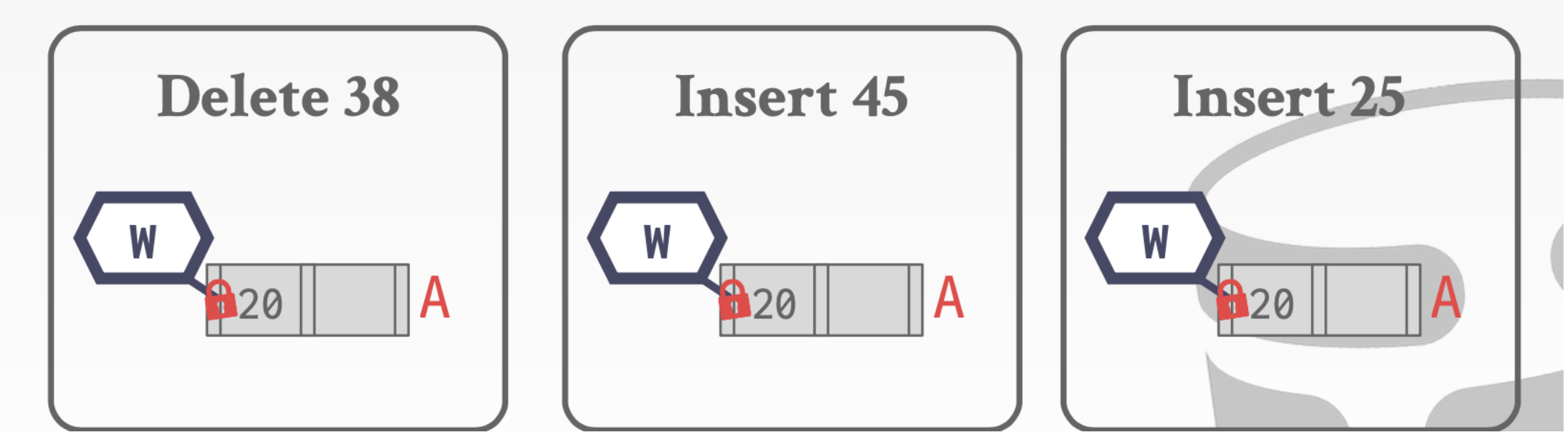
这里要引入乐观🔒
乐观的假设大部分操作是不需要进行合并和分裂的。因此在我们向下的时候都是读Latch而不是写Latch。只有在叶子结点才是write Latch
- 从上到下都是读Latch。而且逐步释放
- 到叶子结点需要修改的时候才为写Latch。这个删除是安全的所以直接结束
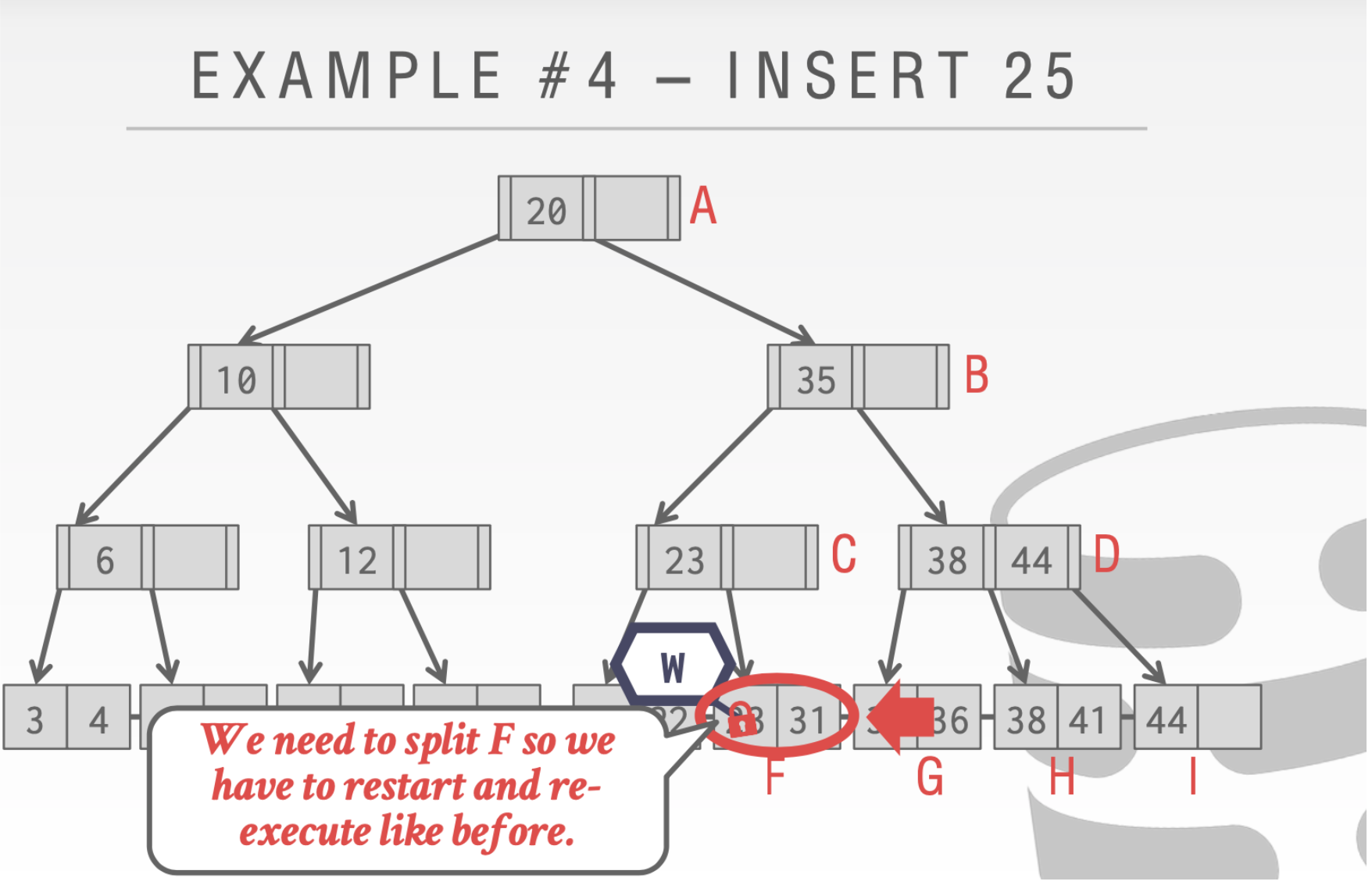
- 当我们到最后一步发现不安全的时候。则需要像上面我们没有引入乐观🔒的时候一样。重新执行一遍
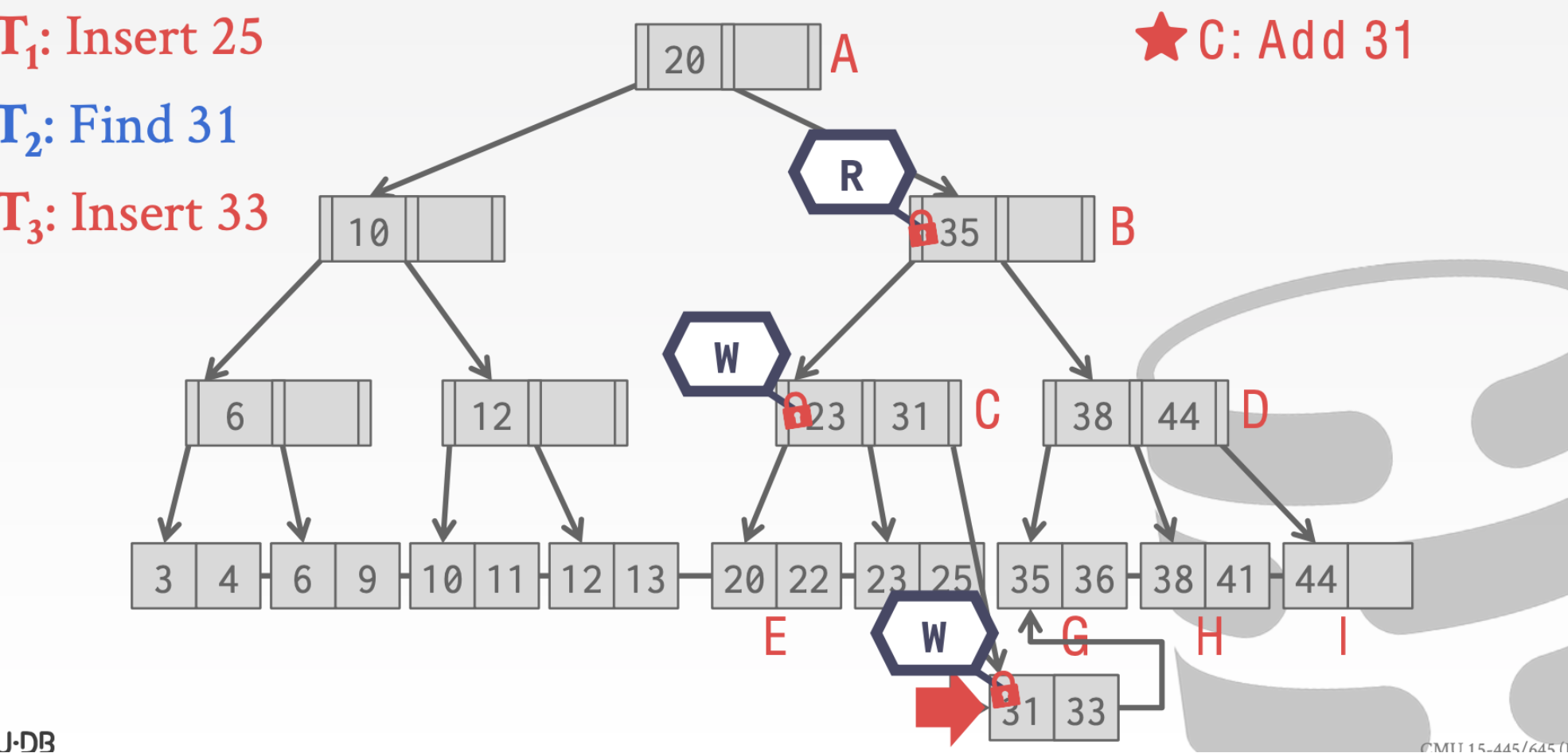
B-Link Tree简介
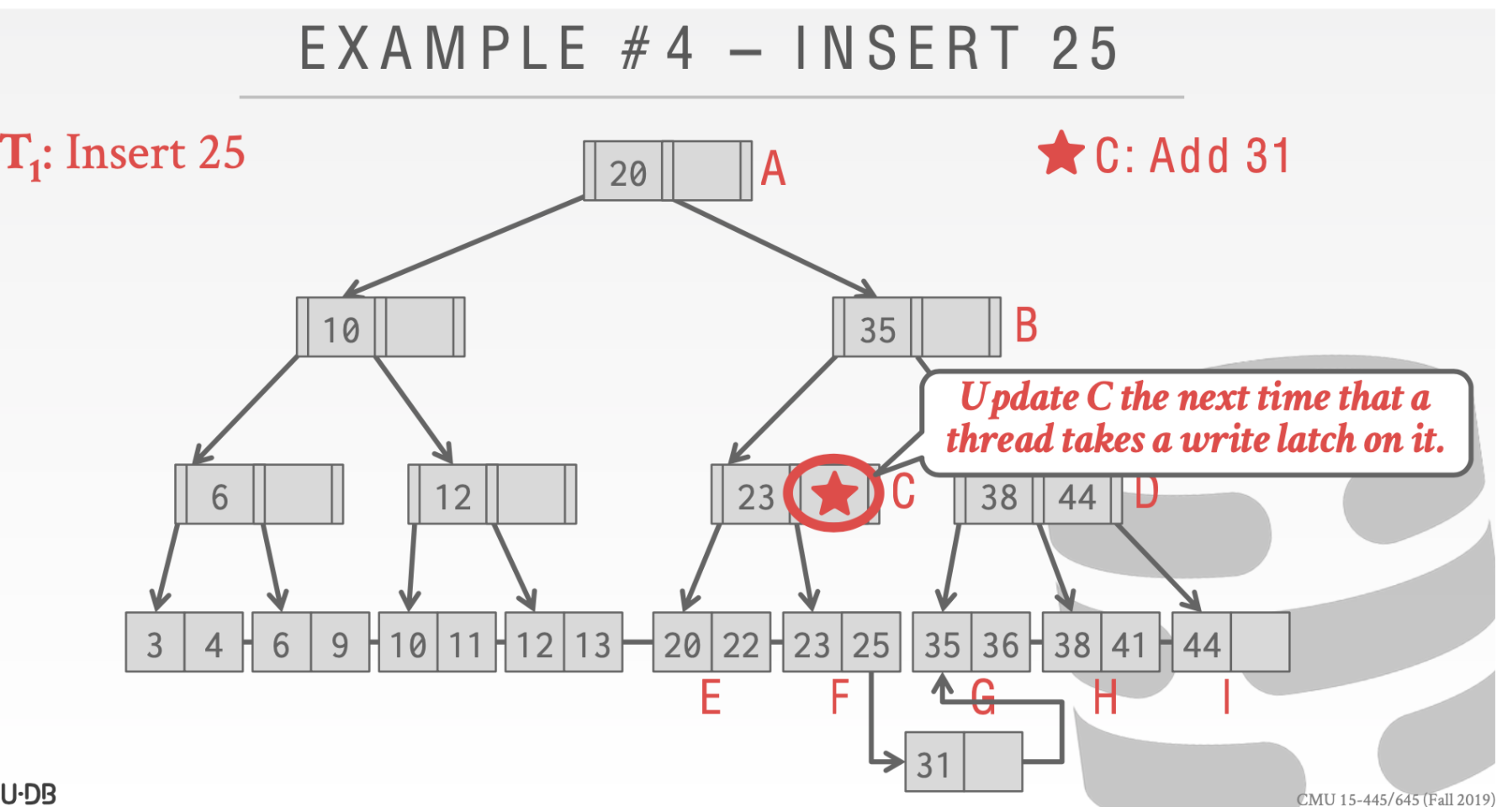
延迟更新父结点
这里用一个🌟来标记这里需要被更新但是还没有执行
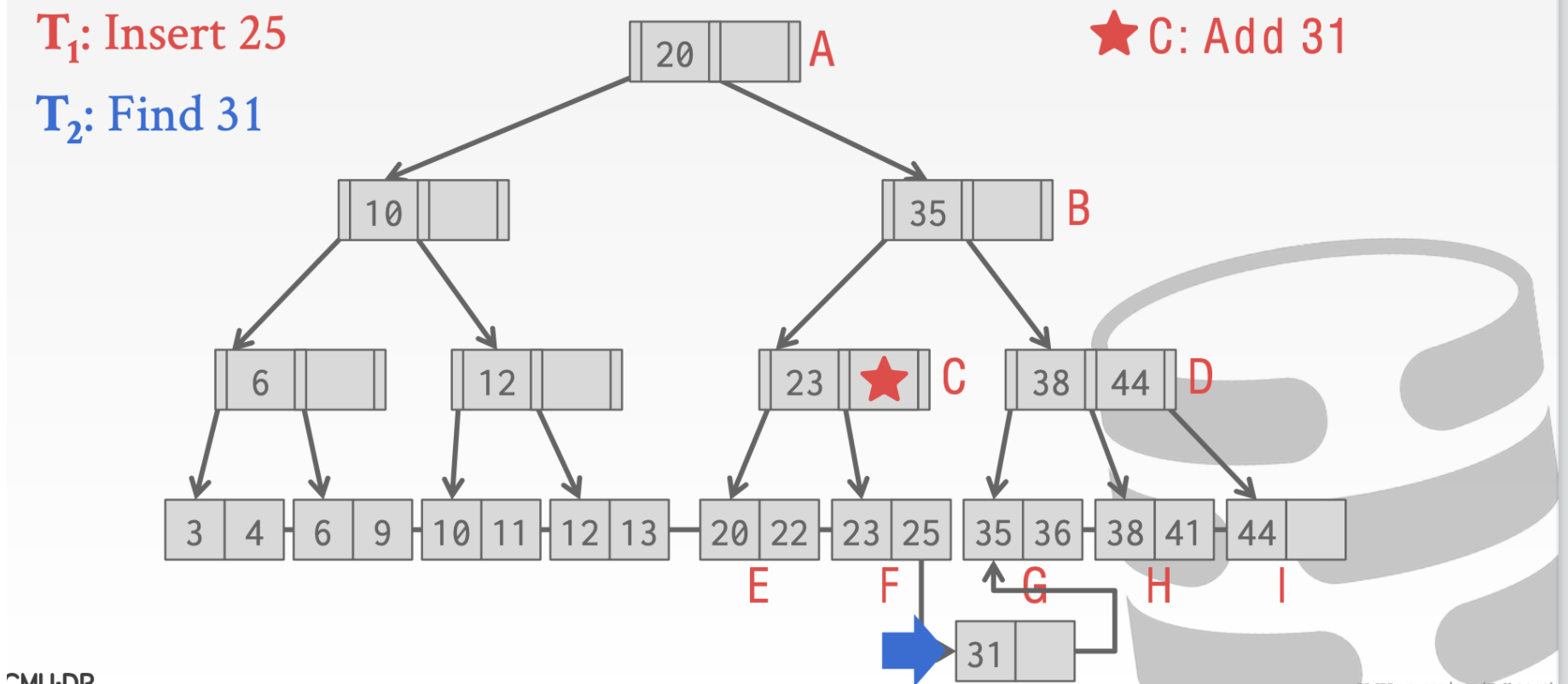
这个时候我们执行其他操作也是正确的比如查找31
这里我们执行insert 33
当执行到结点C的时候。因为这个时候有另一个线程持有了write Latch。所以这个时候🌟操作要执行。随后在插入33
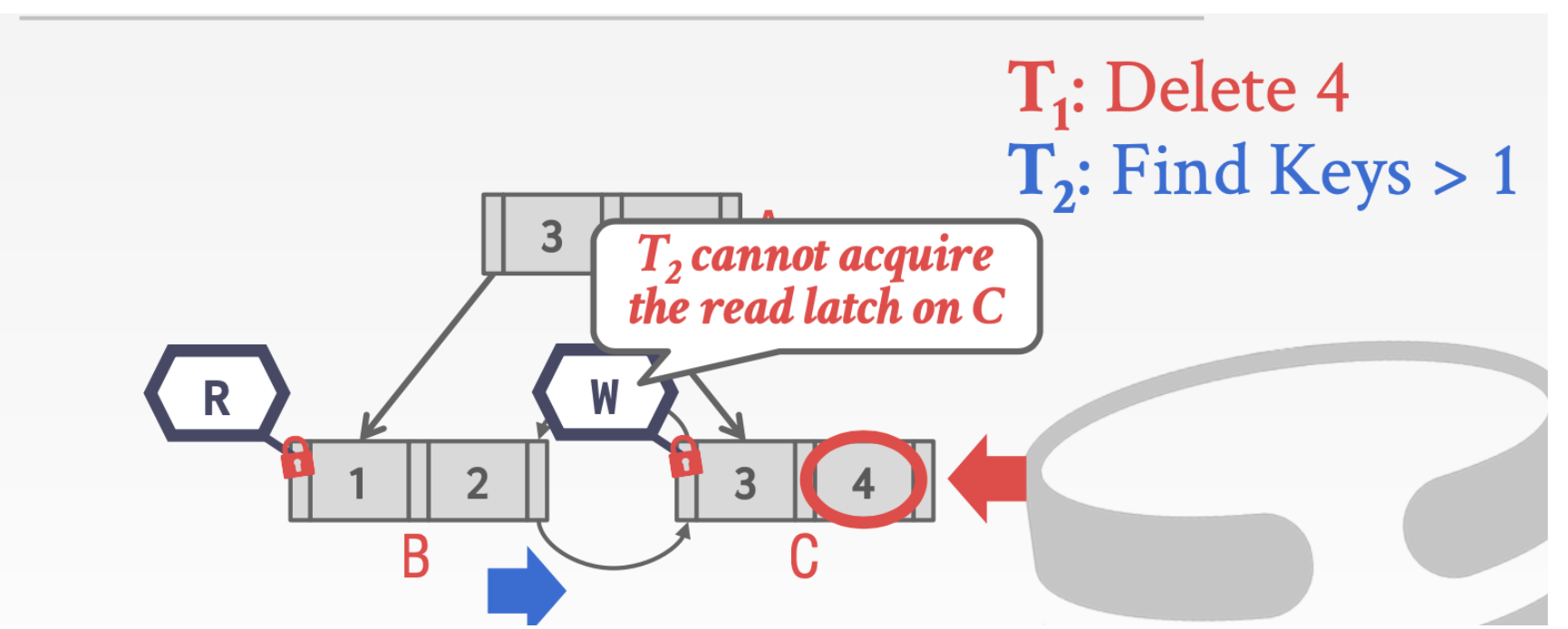
最后一点补充关于扫描操作的
- 线程1在C结点上持有write Latch
- 线程2已经扫描完了结点B想要获得结点C的read Latch
这时候会发生问题,因为线程2无法拿到read Latch
这里有几种解决方法
- 可以等到T1的写操作完成
- 可以重新执行T2
- 可以直接让线程T2停止抢得这个Latch。
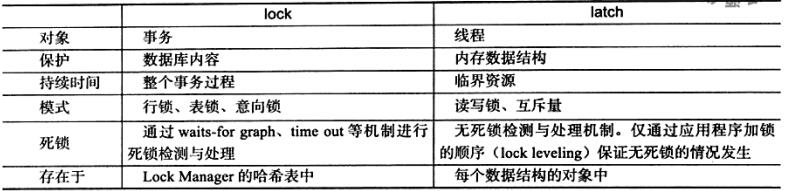
注意这里的Latch和Lock并不一样
6. 辅助函数分析
1. 辅助函数UnlockUnpinPages的实现#
- 如果是读操作则释放read锁
- 否则释放write锁
INDEX_TEMPLATE_ARGUMENTS
void BPLUSTREE_TYPE::
UnlockUnpinPages(Operation op, Transaction *transaction) {
if (transaction == nullptr) {
return;
}
for (auto page:*transaction->GetPageSet()) {
if (op == Operation::READ) {
page->RUnlatch();
buffer_pool_manager_->UnpinPage(page->GetPageId(), false);
} else {
page->WUnlatch();
buffer_pool_manager_->UnpinPage(page->GetPageId(), true);
}
}
transaction->GetPageSet()->clear();
for (const auto &page_id: *transaction->GetDeletedPageSet()) {
buffer_pool_manager_->DeletePage(page_id);
}
transaction->GetDeletedPageSet()->clear();
// if root is locked, unlock it
node_mutex_.unlock();
}
四个自带的解锁和上锁操作
/** Acquire the page write latch. */
inline void WLatch() { rwlatch_.WLock(); }
/** Release the page write latch. */
inline void WUnlatch() { rwlatch_.WUnlock(); }
/** Acquire the page read latch. */
inline void RLatch() { rwlatch_.RLock(); }
/** Release the page read latch. */
inline void RUnlatch() { rwlatch_.RUnlock(); }
这里的rwlatch是自己实现的读写锁类下面来探究一下这个类
由于c++ 并发编程我现在还不太会。。。所以就简单看一下啦后面学完并发编程再补充
-
WLock函数- 首先获取一个锁
- 用一个记号
writer_entered表示是否有写操作 - 如果之前已经有了现在的操作就需要等(这个线程处于阻塞状态)
- 当前如果有其他线程执行读操作。则仍需要阻塞(别人读的时候你不能写)
void WLock() { std::unique_lock<mutex_t> latch(mutex_); while (writer_entered_) { reader_.wait(latch); } writer_entered_ = true; while (reader_count_ > 0) { writer_.wait(latch); } } -
WunLock函数- 写标记置为false
- 然后通知所有的线程
void WUnlock() { std::lock_guard<mutex_t> guard(mutex_); writer_entered_ = false; reader_.notify_all(); } -
RLock函数- 如果当前有人在写或者已经有最多的人读了则阻塞
- 否则只需要让读的计数++
因为是允许多个线程一起读这样并不会出错
void RLock() { std::unique_lock<mutex_t> latch(mutex_); while (writer_entered_ || reader_count_ == MAX_READERS) { reader_.wait(latch); } reader_count_++; } -
RUnLatch函数- 计数--
- 如果当前有人在写并且无人读的话需要通知所有其他线程
- 如果在计数--之前达到了最大读数,释放这个锁之后需要通知其他线程,现在又可以读了。
void RUnlock() { std::lock_guard<mutex_t> guard(mutex_); reader_count_--; if (writer_entered_) { if (reader_count_ == 0) { writer_.notify_one(); } } else { if (reader_count_ == MAX_READERS - 1) { reader_.notify_one(); } } }
7. 并发索引实现
1. FindLeafPageRW的实现
1. 1 整体思路
对于并发控制的实现,采用最简单的latch crabing方法实现,也就是上面讲的那种方法, 这种方法需要在找叶子结点的时候,从根节点到叶子结点的过程需要逐步加锁,然后检测是否能够释放。由于我们的插入和删除操作都需要先找到叶子结点,所以之前使用的无锁版本的FindLeafPage函数在并发条件下就并不适用了。因此这里需要实现一个逐步加锁 + 逐步释放的新函数
- 整体思路和之前的findLeafPage几乎一样,只是多了几次判断
- 如果是读操作,那则直接加锁,然后对上一层释放锁
- 如果是写操作,释放锁之前则要判断一下是否安全。
INDEX_TEMPLATE_ARGUMENTS
Page *BPLUSTREE_TYPE::FindLeafPageRW(const KeyType &key, bool left_most, enum OpType op, Transaction *transaction) {
Page *page = buffer_pool_manager_->FetchPage(root_page_id_); // now root page is pin
BPlusTreePage *node = reinterpret_cast<BPlusTreePage *>(page->GetData());
while (!node->IsLeafPage()) {
if (op == OpType::Read) {
page->RLatch();
UnlatchAndUnpin(op,transaction);
} else {
// else is write op
page->WLatch();
if (IsSafe(node, op)) {
UnlatchAndUnpin(op, transaction);
}
}
transaction->AddIntoPageSet(page);
InternalPage *internal_node = reinterpret_cast<InternalPage *>(node);
page_id_t next_page_id = left_most ? internal_node->ValueAt(0) : internal_node->Lookup(key, comparator_);
Page *next_page = buffer_pool_manager_->FetchPage(next_page_id); // next_level_page pinned
BPlusTreePage *next_node = reinterpret_cast<BPlusTreePage *>(next_page);
page = next_page;
node = next_node;
}
return page;
}
1.2 判断是否安全的函数
- 如果是插入操作,则只要当前node的size处于安全状态即 + 1 之后不会产生分裂,则为安全
- 如果是删除状态。则只要当前node的size - 1 之后不会重分配或者合并,则为安全
- 对于根节点需要进行特殊判断,如果这个根节点是叶子结点则为安全(这种情况随便删)。否则根节点的大小必须大于2(因为如果等于2 ,减去1之后还是1。则是一个没有有效key值的结点,不安全)
INDEX_TEMPLATE_ARGUMENTS
template <typename N>
bool BPLUSTREE_TYPE::IsSafe(N *node, enum OpType op) {
// insert
if (op == OpType::Insert) {
return node->GetSize() < maxSize(node);
}
// remove
if (node->IsRootPage()) {
// If root is a leaf node, no constraint
// If root is an internal node, it must have at least two pointers;
if (node->IsLeafPage()) {
return true;
}
return node->GetSize() > 2;
}
return node->GetSize() > minSize(node);
}
1.3 把释放锁和unpin操作合并
这两个操都要对page做,与其多写几行不如写个函数给他合并在一起做。
transaction->GetPageSet(); 就是之前访问过的page集合
INDEX_TEMPLATE_ARGUMENTS
void BPLUSTREE_TYPE::UnlatchAndUnpin(enum OpType op,Transaction *transaction) const {
if (transaction == nullptr) {
return;
}
auto pages = transaction->GetPageSet();
for (auto page : *pages) {
page_id_t page_id = page->GetPageId();
if (op == OpType::Read) {
page->RUnlatch();
buffer_pool_manager_->UnpinPage(page_id, false);
} else {
page->WUnlatch();
buffer_pool_manager_->UnpinPage(page_id, true);
}
}
pages->clear();
}
2. 支持并发的读写操作
其实只需要之前博客1、2的非并发版本上做一些小小的改动
2.1 支持并发读
2.2 支持并发写
这里要支持插入和删除两种写操作
1. 插入
-
根据实验提示,首先需要获取对于根节点的锁。我个人认为是为了防止下面这种情况发生
如果理解的有问题,欢迎大家指出,互相讨论
consider the following case
txn A read "A" from tree but not hold mutex (if "A" not in the tree)
before A crab page0 latch , txnB crab page0 and insert "A" into the tree then unlatch page0
txnA crab page0 get false result
-
用
FindLeafRW替换之前的FindLeaf函数即可 -
用
UnLatchAndPin替换之前简单的unpin操作。
完整代码就不贴了,在之前的insert上改一下就行了
2. 删除
- 对于删除首先要在remove上做和insert一样的处理
- 在核心函数
CoalesceOrRedistribute中对兄弟结点做修改之前,先加写锁结束之后释放写锁就ok