B+树详解+代码实现(插入篇)
为了cmu数据库的Lab2作准备
1. B-Tree Family
→ B-Tree (1971)
→ B+Tree (1973)
→ B*Tree (1977?)
→ B link-Tree (1981)
2. B+ Tree的特性
- 完美平衡树
- 根结点至少有两个子女。
- 除了根结点以外的其他结点的关键字个数 $ \frac{m}{2} \le keys \le m-1 $。
- 内部结点有k个关键字就会有k+1个孩子
- 叶结点会用双向链表连接起来。因为所有的value都保存在叶子结点。其他结点只保存索引,这样可以支持顺序索引和随机索引
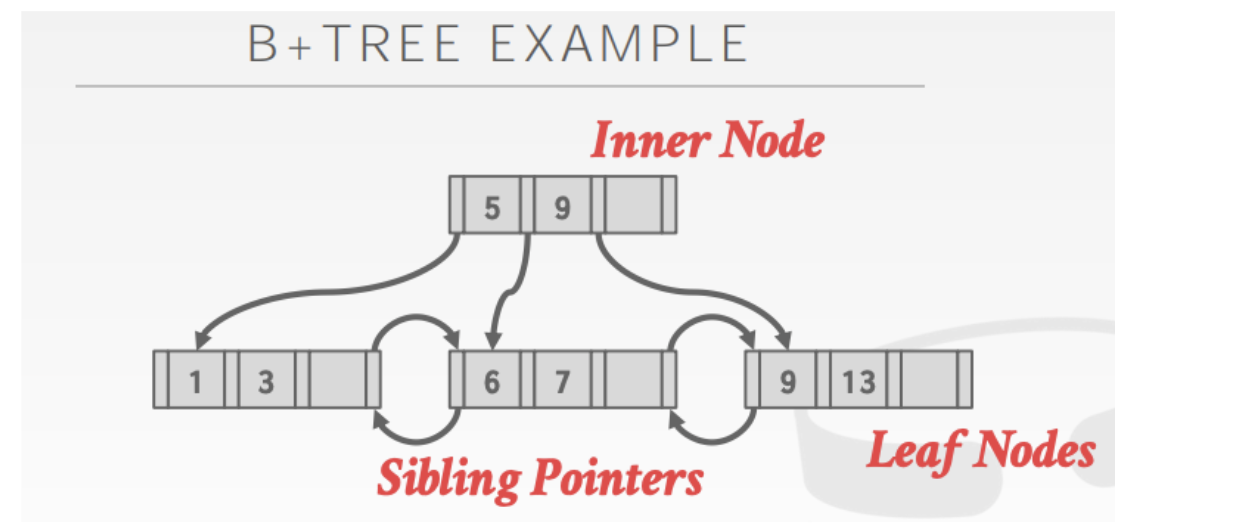
正常来讲b+树的所有元素都需要在叶子结点出现。
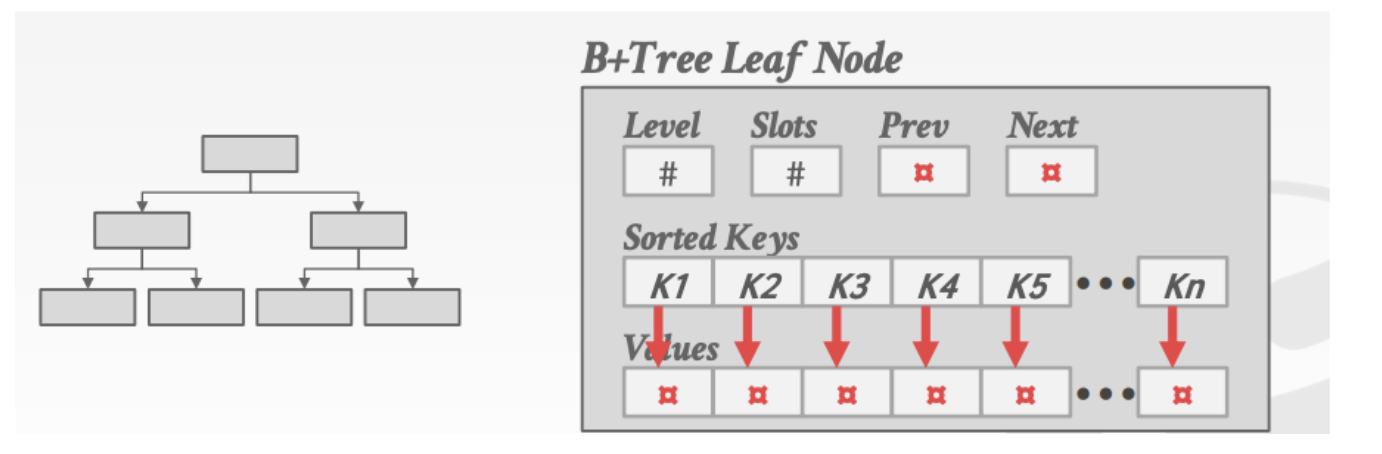
对于叶子结点的存储有两种形式
一种是存指针。一种存数据
- Record IDs: A pointer to the location of the tuple
- Tuple Data: The actual contents of the tuple is stored in the leaf node
3. B+ Tree 的插入
3.1 算法原理
-
若为空树,创建一个叶子结点,然后将记录插入其中,此时这个叶子结点也是根结点,插入操作结束。
-
针对叶子类型结点:根据key值找到叶子结点,向这个叶子结点插入记录。插入后,若当前结点key的个数小于等于m-1,则插入结束。否则将这个叶子结点分裂成左右两个叶子结点,左叶子结点包含前m/2个记录,右结点包含剩下的记录,将第m/2+1个记录的key进位到父结点中(父结点一定是索引类型结点),进位到父结点的key左孩子指针向左结点,右孩子指针向右结点。将当前结点的指针指向父结点,然后执行第3步。
-
针对索引类型结点(内部结点):若当前结点key的个数小于等于m-1,则插入结束。否则,将这个索引类型结点分裂成两个索引结点,左索引结点包含前\(\frac{(m-1)}{2}\)个key,右结点包含\(m- \frac{(m-1)}{2}\)个key,将第\(\frac{m}{2}\)个key进位到父结点中,进位到父结点的key左孩子指向左结点, 进位到父结点的key右孩子指向右结点。将当前结点的指针指向父结点,然后重复这一步。
cmu这里给了演示网站 https://www.cs.usfca.edu/~galles/visualization/BPlusTree.html
假设我们要插入5, 8,10,15 ,16 , 20 ,19 。以m=3为例子
- 插入5,8直接根节点
-
插入10
由于此时根节点有3个结点>2(m-1)因此会分裂。而且这个时候是对叶子类型结点的处理。把前m/2=1个结点分给左叶子。右叶子包含剩下的结点。中间的 m/2+1第二个结点成为父节点。
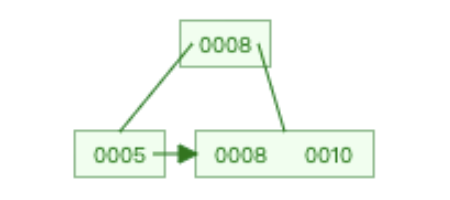
-
插入15。15会插到根节点的右边。然后就会出现和上面一样的情况。因此我们继续分裂
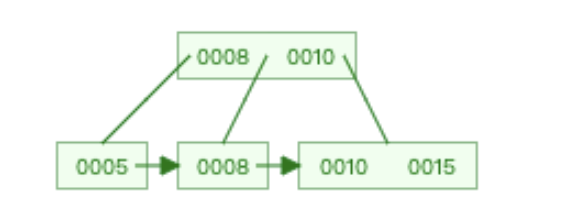
-
插入16
- 先插入到15的右边,导致15所在的叶子结点分裂。会把15提到父节点。10成为左孩子,15 ,16为右孩子
- 递归向上检查。会发现父节点有8,10,15三个结点也不符合要求。因此需要再次进行分裂。
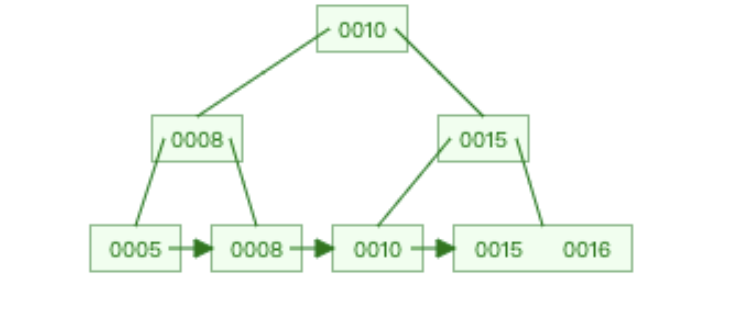
-
插入20
20 会放到16的右边。然后这个结点需要分裂。15成为左孩子,16 ,20 成为右孩子,16提为父结点就ok啦
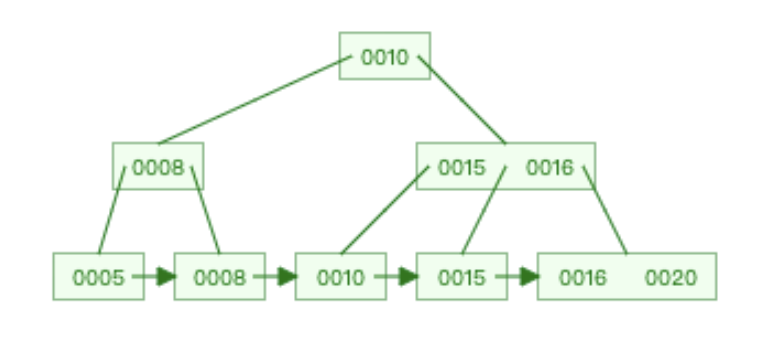
-
插入19
- 会放到16左边20右边。因此这个结点会分裂,把19提到父节点
- 递归检查的时候发现父节点也有三个结点这里也需要分裂
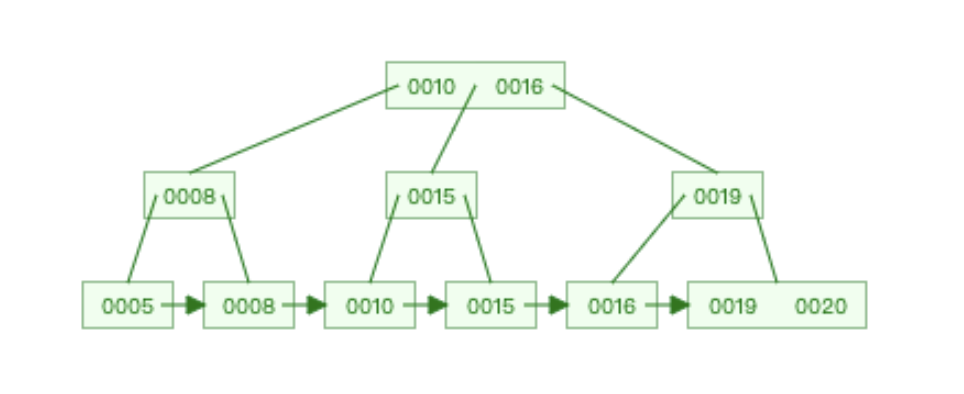
好了关于b+树的插入模拟我们就到这里了。下面来写一下代码
3.2 代码实现
一些在b+树插入时代码的时候思考的问题
-
split的时候需要找父结点怎么解决
一种是维护一个parent指针
-
查找插入结点
-
维护关键字有序如何做
因为用的数组存的关键字。所以就按照数组插入o(n)的复杂度
3.21 数据结构设计
- 用
*key表示关键字 - 用
**ptr表示结点 - 用
IS_LEAF来表示是否为页子结点。
#include <iostream>
#include <queue>
using namespace std;
int MAX = 2;
// BP node
class Node {
bool IS_LEAF;
int *key, size;
Node** ptr;
Node* parent;
friend class BPTree;
public:
Node():key(new int[MAX+1]),ptr(new Node* [MAX+1]),parent(NULL){}
~Node();
};
// BP tree
class BPTree {
Node* root;
void insertInternal(int,Node*,Node*,Node*);
void split(int ,Node *,Node *);
int insertVal(int ,Node *);
public:
BPTree():root(NULL){}
void insert(int x);
void display();
};
3.22 普通插入
insertVal函数负责找到插入的位置并返回
int BPTree::insertVal(int x, Node *cursor) {
int i = 0;
while (x > cursor->key[i] && i < cursor->size) i++;
for (int j = cursor->size; j > i; j--) cursor->key[j] = cursor->key[j - 1];
cursor->key[i] = x;
cursor->size++;
return i;
}
insert函数负责进行插入这里分为几种情况
- 根节点为空则创建一个根节点。
- 如果不为根节点则要找到插入位置(到叶结点才停止)同时记录插入结点的父结点
- 如果插入结点满足关键字个数<MAX( 就是M-1) 我们就可以直接插入。
- 否则需要
split
void BPTree::insert(int x) {
if (root == NULL) {
root = new Node;
root->key[0] = x;
root->IS_LEAF = true;
root->size = 1;
root->parent = NULL;
} else {
Node *cursor = root;
Node *parent;
while (cursor->IS_LEAF == false) {
parent = cursor;
for (int i = 0; i < cursor->size; i++) {
if (x < cursor->key[i]) {
cursor = cursor->ptr[i];
break;
}
if (i == cursor->size - 1) {
cursor = cursor->ptr[i + 1];
break;
}
}
}
if (cursor->size < MAX) {
insertVal(x,cursor);
cursor->parent = parent;
cursor->ptr[cursor->size] = cursor->ptr[cursor->size - 1];
cursor->ptr[cursor->size - 1] = NULL;
} else split(x, parent, cursor);
}
}
3.23 需要split的插入
这里要分两种情况
- 叶子结点拆分之后。提上去的结点为根节点
- 否则需要调用
insertInternal函数
void BPTree::split(int x, Node * parent, Node *cursor) {
Node* LLeaf=new Node;
Node* RLeaf=new Node;
insertVal(x,cursor);
LLeaf->IS_LEAF=RLeaf->IS_LEAF=true;
LLeaf->size=(MAX+1)/2;
RLeaf->size=(MAX+1)-(MAX+1)/2;
for(int i=0;i<MAX+1;i++)LLeaf->ptr[i]=cursor->ptr[i];
LLeaf->ptr[LLeaf->size]= RLeaf;
RLeaf->ptr[RLeaf->size]= LLeaf->ptr[MAX];
LLeaf->ptr[MAX] = NULL;
for (int i = 0;i < LLeaf->size; i++) {
LLeaf->key[i]= cursor->key[i];
}
for (int i = 0,j=LLeaf->size;i < RLeaf->size; i++,j++) {
RLeaf->key[i]= cursor->key[j];
}
if(cursor==root){
Node* newRoot=new Node;
newRoot->key[0] = RLeaf->key[0];
newRoot->ptr[0] = LLeaf;
newRoot->ptr[1] = RLeaf;
newRoot->IS_LEAF = false;
newRoot->size = 1;
root = newRoot;
LLeaf->parent=RLeaf->parent=newRoot;
}
else {insertInternal(RLeaf->key[0],parent,LLeaf,RLeaf);}
}
3.24 insertInternal插入的实现
基本思路都是差不多的。就是需要注意递归调用
- 如果由于拆分之后提上去的结点不会再产生拆分则直接插入
- 再拆如果提到根节点则创建新的根节点
- 否则就继续调用
insertInternal
void BPTree::insertInternal(int x,Node* cursor,Node* LLeaf,Node* RRLeaf)
{
if (cursor->size < MAX) {
auto i=insertVal(x,cursor);
for (int j = cursor->size;j > i + 1; j--) {
cursor->ptr[j]= cursor->ptr[j - 1];
}
cursor->ptr[i]=LLeaf;
cursor->ptr[i + 1] = RRLeaf;
}
else {
Node* newLchild = new Node;
Node* newRchild = new Node;
Node* virtualPtr[MAX + 2];
for (int i = 0; i < MAX + 1; i++) {
virtualPtr[i] = cursor->ptr[i];
}
int i=insertVal(x,cursor);
for (int j = MAX + 2;j > i + 1; j--) {
virtualPtr[j]= virtualPtr[j - 1];
}
virtualPtr[i]=LLeaf;
virtualPtr[i + 1] = RRLeaf;
newLchild->IS_LEAF=newRchild->IS_LEAF = false;
//这里和叶子结点上有区别的
newLchild->size= (MAX + 1) / 2;
newRchild->size= MAX - (MAX + 1) /2;
for (int i = 0;i < newLchild->size;i++) {
newLchild->key[i]= cursor->key[i];
}
for (int i = 0, j = newLchild->size+1;i < newRchild->size;i++, j++) {
newRchild->key[i]= cursor->key[j];
}
for (int i = 0;i < LLeaf->size + 1;i++) {
newLchild->ptr[i]= virtualPtr[i];
}
for (int i = 0, j = LLeaf->size + 1;i < RRLeaf->size + 1;i++, j++) {
newRchild->ptr[i]= virtualPtr[j];
}
if (cursor == root) {
Node* newRoot = new Node;
newRoot->key[0]= cursor->key[newLchild->size];
newRoot->ptr[0] = newLchild;
newRoot->ptr[1] = newRchild;
newRoot->IS_LEAF = false;
newRoot->size = 1;
root = newRoot;
newLchild->parent=newRchild->parent=newRoot;
}
else {
insertInternal(cursor->key[newLchild->size],cursor->parent,newLchild,newRchild);
}
}
}
3.25 展示函数的实现
这里用了一个简单的层次遍历。来实现展示函数
void BPTree::display() {
queue<Node*>q;
q.push(root);
while(!q.empty()){
int size_t=q.size();
while(size_t--){
auto t=q.front();
for(int i=0;i<t->size+1;i++){
if(!t->IS_LEAF){
q.push(t->ptr[i]);
}
}
for(int i=0;i<t->size;i++){
cout<<t->key[i]<<",";
}
cout<<" ";
q.pop();
}
cout<<endl;
}
}
3.26 结果
假设我们要插入5, 8,10,15 ,16 , 20 ,19。以m=3(MAX=2)为例子
得到的结果如下
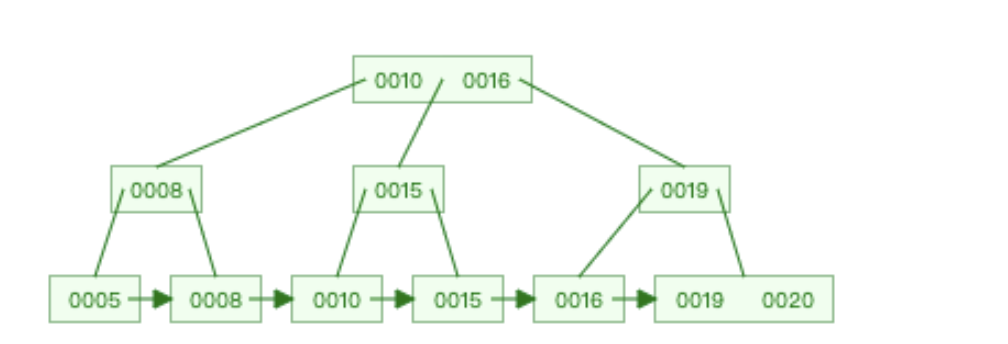
程序运行结果如下
,表示在一个结点内
三个空格表示不同的结点

可以发现代码是正确的。完整的代码见下面的GitHub地址


