菜鸡数据结构

数据结构复习

一个月学完数据结构，写一篇究极总结，当复习了

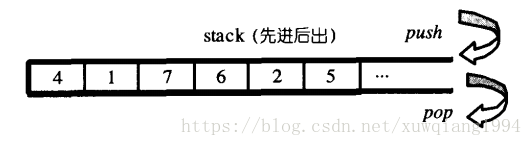
栈(Stack)

回归原始，可以用链表实现栈，或者说所有的数据结构都可以用链表实现。STL中用stack容器实现栈。栈的特征就是先进后出，First In Last Out。

template <class T, class Container = deque > class stack;

T就是栈所存的元素类型，container是容器适配器，不写第二个参数的情况下默认是deque，你也可以自己把它换成vector，具体搜索容器适配器，这里不多赘述。
需要注意的一点是，stack没有迭代器，不允许遍历，只能在栈顶进行push、top、pop操作。

常用函数

size()返回栈内元素数量，类型是unsigned integral。
empty()用于判断栈内有无元素（stack.size() == 0），是否为空，返回bool值。
top()用于返回栈顶元素的引用。
push(value_type)和emplace(arg...)都是在栈顶插入元素，区别在于push是直接插入对象，在传参数的时候是一个对象。而emplace可以跟push一样，直接插入对象，也可以直接传入构造对象需要的元素，然后自己调用其构造函数。这么说应该说不明白，举个例子：
我有一个类

class Data {
private:
	int a, b;
public:
	Data(int x, int y) :a(x), b(y) {};
};

现在声明一个栈，类型是Data

	stack<Data> nums;

下面分别用push和emplace插入元素

	nums.push(Data(1, 2));     //先调用Data的构造函数，创建出对象之后再压入栈顶，参数是个右值
	nums.emplace(Data(1, 2));  //同上
	nums.emplace(1, 2);        //先调用Data的构造函数，传进去的参数用于Data的构造函数，把对象建好之后再压入栈

可以看出来emplace拥有push一样的功能，但是它还能调用对象的构造函数，十分强大。
pop();用于删除栈顶元素，没有返回值。
swap(stack2)用于将一个堆栈的内容与另一个相同类型的堆栈交换，但是大小可能会有所不同，没有返回值。

队(Queue)

STL中使用queue容器实现栈。跟栈不一样，队是先进先出，First In First Out。

template <class T, class Container = deque > class queue;

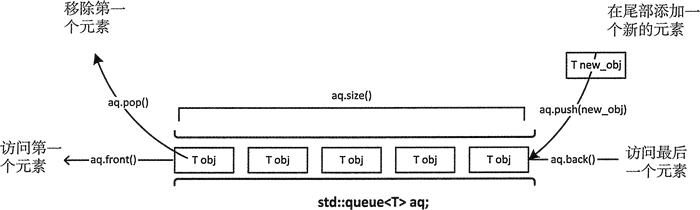
跟stack一样，T是容器的类型，container是适配器，默认deque。queue同样没有迭代器，只能通过一些函数在队首、队尾操作。
STL的queue就不说了，用起来跟stack差不多，一些api百度一下就好了。

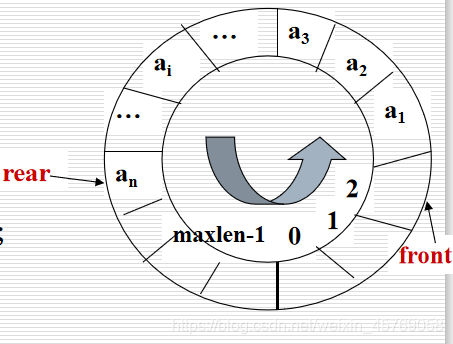
循环队列

跟栈不一样的是，队还有一个问题：循环队列。想像一下，一条蛇围成一个圆，嘴巴咬着尾巴，这个就是循环队列的样子。

下面写一下循环队列：

#pragma once

template <class T>
class CircularQueue {
	int rear, front;
	int maxSize;
	T* queue;

	bool Full() const;
public:
	CircularQueue();
	CircularQueue(int size);
	~CircularQueue();

	bool Push(const T& data);
	T Top() const;
	T Bottom() const;
	bool Empty() const;
	bool Pop();
	void Clear();
	int Size() const;
};

template<class T>
bool CircularQueue<T>::Full() const {
	return ((rear + 1) % maxSize == front) ? true : false;
}

template<class T>
CircularQueue<T>::CircularQueue() {
	front = rear = 0;
	maxSize = 10;
	queue = new T[maxSize];
}

template <class T>
CircularQueue<T>::CircularQueue(int size) :front(0), rear(0), maxSize(size + 1) {
	queue = new T[maxSize];
}

template<class T>
CircularQueue<T>::~CircularQueue() {
	delete[] queue;
}

template <class T>
bool CircularQueue<T>::Push(const T& data) {
	if (Full()) {
		return false;
	}
	queue[rear] = data;
	rear = (rear + 1) % maxSize;
	return true;
}

template<class T>
T CircularQueue<T>::Top() const {
	if (Empty()) {
		return T();
	}
	return queue[front];
}

template<class T>
T CircularQueue<T>::Bottom() const {
	if (Empty()) {
		return T();
	}
	return queue[rear];
}

template<class T>
bool CircularQueue<T>::Empty() const {
	return(front == rear) ? true : false;
}

template<class T>
bool CircularQueue<T>::Pop() {
	if (Empty()) {
		return false;
	}
	front = (front + 1) % (maxSize);
	return true;
}

template<class T>
void CircularQueue<T>::Clear() {
	front = rear = 0;
}

template<class T>
int CircularQueue<T>::Size() const {
	return (rear - front + maxSize) % maxSize;
}

把大致功能都实现了一遍，代码有参考。总结一下循环队列的关键点：

循环列表最关键的是处理队头队尾指针，不能一直加一直减，所以就用到了求余的方法
判断是否为空：front == rear
判断是否已满：(rear + 1) % maxSize == front
求元素个数：(rear - front + maxSize) % maxSize

哈希表(Hash Table)

哈希表又叫散列表，它储存数据是通过键值对进行的。关于键值对，可以想象你在逛商场买衣服，每一件衣服上都挂着一个吊牌，你每次都是拿吊牌，然后吊牌的绳子把衣服拉起来，吊牌就是键，衣服就是值。但是哈希表最大的不同在于，它的键是经过处理的：哈希表的键通过散列函数映射到某一集合，比如f(key)=a*key+b，通过散列函数映射之后得到的键就不是原来的键了。根据哈希表的种种特征，很容易看出来哈希表里面没有重复的键，但是一个键可以对应多个值，具体看你怎么使用了。

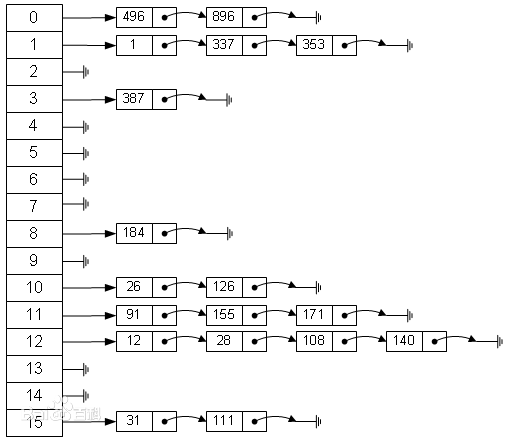
你可能会问这样做有什么用，试想一些键非常大，或者很分散，你存起来会消耗很多内存，耗时也久。但是经过散列函数映射到一个范围里面，就能加快效率，减少开销。但是哈希表这么好用，自然也会有缺陷的：万一经过散列函数之后，某一些键映射到同一个地方怎么办？这就是哈希冲突。
解决的办法也有很多，开放寻址法（线性探测法、平方探测法）、链地址法、再散列法等。
稍微写一下简单的哈希表：

#define MAXTABLESIZE 10000
#define KEYLENGTH 100

struct LNode {
	int data;
	LNode* next;
	LNode() :data(0), next(nullptr) {};
};

struct HashTable {
	int tablesize;
	LNode* heads;
	HashTable() :tablesize(0), heads(nullptr) {};
};

/// <summary>
/// 返回大于n且不超过MAXTABLESIZE的最小质数
/// </summary>
/// <param name="n">起始值</param>
/// <returns>质数</returns>
int NextPrime(int n) {
	int p = (n % 2) ? n + 2 : n + 1;
	int i = 0;
	while (p <= MAXTABLESIZE) {
		for (i = (int)sqrt(p); i > 2; i--) {
			if ((p % i) == 0) {
				break;
			}
		}
		if (i == 2) {
			break;
		}
		else {
			p += 2;
		}
	}
	return p;
}

/// <summary>
/// 创建哈希表
/// </summary>
/// <param name="table_size">表长度</param>
/// <returns>表头指针</returns>
HashTable* CreateTable(int table_size) {
	HashTable* h = (HashTable*)malloc(sizeof(HashTable));
	h->tablesize = NextPrime(table_size);
	h->heads = (LNode*)malloc(h->tablesize * sizeof(LNode));
	for (int i = 0; i < h->tablesize; i++) {
		h->heads[i].next = nullptr;
	}
	return h;
}

/// <summary>
/// 散列函数
/// </summary>
/// <param name="key">键</param>
/// <param name="n">链表长度</param>
/// <returns>键值</returns>
int Hash(int key, int n) {
	return key % n;
}

/// <summary>
/// 查找元素
/// </summary>
/// <param name="h">表头指针</param>
/// <param name="key">要找的键</param>
/// <returns>找到元素的指针</returns>
LNode* Find(HashTable* h, int key) {
	int pos = Hash(key, h->tablesize);
	LNode* p = h->heads[pos].next;
	while (p && key != p->data) {
		p = p->next;
	}
	return p;
}

/// <summary>
/// 插入新元素
/// </summary>
/// <param name="h">表头</param>
/// <param name="key">插入的键</param>
/// <returns>是否完成</returns>
bool Insert(HashTable* h, int key) {
	LNode* p = Find(h, key);
	if (!p) {
		LNode* newNode = (LNode*)malloc(sizeof(LNode));
		newNode->data = key;
		int pos = Hash(key, h->tablesize);
		newNode->next = h->heads[pos].next;
		h->heads[pos].next = newNode;
		return true;
	}
	else {
		return false;
	}
}

/// <summary>
/// 移除元素
/// </summary>
/// <param name="h">表头</param>
/// <param name="key">要删除的键</param>
/// <returns>是否完成</returns>
bool Remove(HashTable* h, int key) {
	LNode* p0 = Find(h, key);
	if (p0) {
		int pos = Hash(key, h->tablesize);
		LNode* p = h->heads[pos].next;
		if (p == p0) {
			h->heads[pos].next = p->next;
			p->next = nullptr;
			free(p);
			return true;
		}
		while (p && p->next != p0) {
			p = p->next;
		}
		p->next = p0->next;
		p0->next = nullptr;
		free(p0);
		return true;
	}
	else {
		return false;
	}
}

/// <summary>
/// 销毁链表
/// </summary>
/// <param name="h">表头元素</param>
void DestroyTable(HashTable* h) {
	LNode* p, * temp;
	for (int i = 0; i < h->tablesize; i++) {
		p = h->heads[i].next;
		while (p) {
			temp = p->next;
			free(p);
			p = temp;
		}
	}
	free(h->heads);
	free(h);
}

代码有参考。上面就实现了一个基于链表的哈希表，解决哈希冲突的方法是线性探测，直接加一。
STL中使用unordered_map实现哈希表。

template <class Key, class T, class Hash = hash, class Pred = equal_to, class Alloc = allocator<pair<const Key, T>>> class unordered_map;
关于hash_map与unordered_map：
由于在C++标准库中没有定义散列表hash_map，标准库的不同实现者将提供一个通常名为hash_map的非标准散列表。因为这些实现不是遵循标准编写的，所以它们在功能和性能保证上都有微妙的差别。
从C++11开始，哈希表实现已添加到C++标准库标准。决定对类使用备用名称，以防止与这些非标准实现的冲突，并防止在其代码中有hash_table的开发人员无意中使用新类。
所选择的备用名称是unordered_map，它更具描述性，因为它暗示了类的映射接口和其元素的无序性质。

Key就是键的类型，T就是值的类型，Hash就是散列函数，Pred是一个二元谓词，用来判断键是否已经存在的，Alloc是分配器。散列函数、谓词和分配器都用默认的就好，我们一般只用定义键和值的类型。需要强调的是哈希表是无序容器，迭代器之间不能用大于小于号比较，可以与队和栈做对比。
一些api也是百度去看吧，做一道简单LeetCode示范一下：

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
		if (nums.size() < 2) {
			return {};
		}
		unordered_map<int, int> hashtable;
		for (int i = 0; i < nums.size(); i++) {
			if (hashtable.find(nums[i]) != hashtable.end()) {
				return { hashtable[nums[i]],i };
			}
			hashtable[target - nums[i]] = i;
		}
		return {};
    }
};

哈希去重还是很好用的，看到题目说没有重复就多想想哈希。

二叉树(Binary Tree)

二叉树是一种非常重要的数据结构，许多实际问题抽象出来的数据结构都是二叉树，或者说是树。

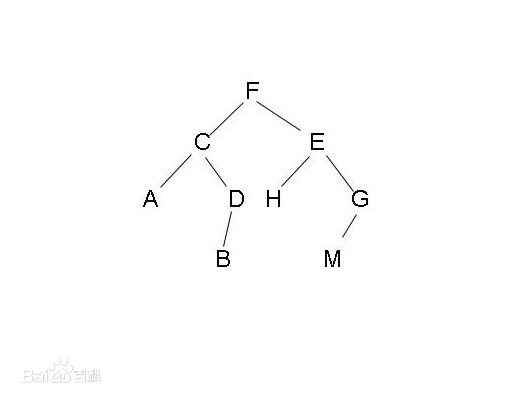
不知道有没有发现，之前的栈、队、哈希表的数据元素前后关系都是一对一的，再看到二叉树，它是一对多的，如果继续往下学，图的数据结构是多对多的，所以二叉树开始就是非线性结构的数据结构了。

基本术语和性质

先介绍一下二叉树相关的术语：二叉树顶端称为根节点，二叉树的节点包含一个数据元素及指向其左、右子树的两个分支，分别成为左分支和右分支。节点的左、右子树的根称为该节点的左、右孩子，统称为孩子，该节点称为孩子的双亲。同一个孩子之间可互称为兄弟。节点的孩子个数称为节点的度，度为0的节点称为叶子节点，非叶子节点的结构称为内部结构或分支节点。节点的层次从根节点开始定义，根为第1层，根的孩子为第2层，如此类推。二叉树中节点的最大层次称为二叉树的深度或高度。一棵深度为k且有 2^k-1个节点的二叉树称为满二叉树。一棵深度为k的有n个结点的二叉树，对树中的结点按从上至下、从左到右的顺序进行编号，如果编号为i（1≤i≤n）的结点与满二叉树中编号为i的结点在二叉树中的位置相同，则这棵二叉树称为完全二叉树。
应该看晕了吧，下面上点图：

层的定义

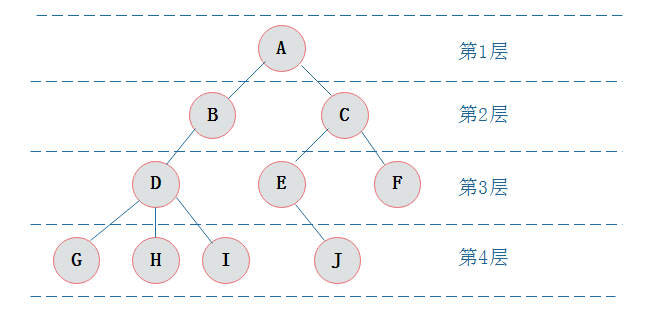
度的定义

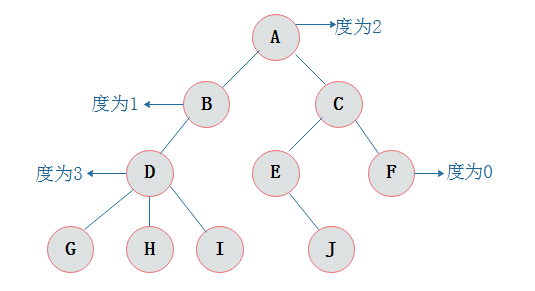
满二叉树的定义

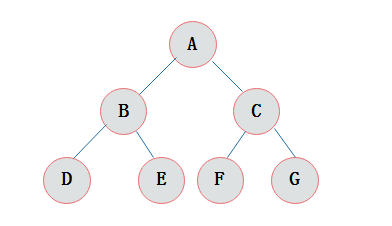
完全二叉树的定义

最后再补充一下二叉树的性质，这些性质对后面的使用会很有帮助：

存储与遍历

上面那些只不过是二叉树的术语，下面才是这个数据结构的使用。
在存储二叉树时，除了存储它的每个节点数据以外，还要表示节点之间的一对多逻辑，也就是父子关系。根据二叉树的性质5，我们可以用一维数组去存储完全二叉树，每个节点的双亲和孩子都可以根据性质5计算得出。

但是一般的二叉树就不太方便用一维数组存了，因此我们可以定义自己的数据结构。

#pragma once
#include<iostream>
#include<queue>

template<typename T>
struct TreeNode {
	T data;
	TreeNode<T>* leftChild, * rightChild;
	TreeNode() {}
	TreeNode(T x) : data(x), leftChild(nullptr), rightChild(nullptr) {}
};

template<typename T>
class BinaryTree {
private:
	TreeNode<T>* root;

	void DeleteNode(TreeNode<T>* head);
	void InsertNode(const T& x, TreeNode<T>*& head);
	void Pre(TreeNode<T>* head) const;		// 前序遍历
	void In(TreeNode<T>* head) const;		// 中序遍历
	void Post(TreeNode<T>* head) const;		// 后序遍历
public:
	BinaryTree() :root(nullptr) {};
	BinaryTree(const T& data);
	~BinaryTree();

	void Insert(const T& x);
	void PreTraversal() const;
	void InTraversal() const;
	void PostTraversal() const;
};

template<typename T>
void BinaryTree<T>::DeleteNode(TreeNode<T>* head) {
	if (head != nullptr) {
		DeleteNode(head->leftChild);
		DeleteNode(head->rightChild);
		delete head;
	}
}

template<typename T>
void BinaryTree<T>::InsertNode(const T& x, TreeNode<T>*& head) {
	if (head == nullptr) {
		head = new TreeNode<T>(x);
		return;
	}

	std::queue<TreeNode<T>*> level;
	TreeNode<T>* temp;
	level.push(head);
	while (!level.empty()) {
		temp = level.front();
		level.pop();

		if (temp->leftChild) {
			level.push(temp->leftChild);
		}
		else {
			InsertNode(x, temp->leftChild);
			break;
		}

		if (temp->rightChild) {
			level.push(temp->rightChild);
		}
		else {
			InsertNode(x, temp->rightChild);
			break;
		}
	}
}

template<typename T>
void BinaryTree<T>::Pre(TreeNode<T>* head) const {
	if (head != nullptr) {
		std::cout << head->data << " ";
		Pre(head->leftChild);
		Pre(head->rightChild);
	}
}

template<typename T>
void BinaryTree<T>::In(TreeNode<T>* head) const {
	if (head != nullptr) {
		In(head->leftChild);
		std::cout << head->data << " ";
		In(head->rightChild);
	}
}

template<typename T>
void BinaryTree<T>::Post(TreeNode<T>* head) const {
	if (head != nullptr) {
		Post(head->leftChild);
		Post(head->rightChild);
		std::cout << head->data << " ";
	}
}

template<typename T>
BinaryTree<T>::BinaryTree(const T& data) {
	root = new TreeNode<T>(data);
}

template<typename T>
BinaryTree<T>::~BinaryTree() {
	DeleteNode(root);
}

template<typename T>
void BinaryTree<T>::Insert(const T& x) {
	InsertNode(x, root);
}

template<typename T>
void BinaryTree<T>::PreTraversal() const {
	Pre(root);
}

template<typename T>
void BinaryTree<T>::InTraversal() const {
	In(root);
}

template<typename T>
void BinaryTree<T>::PostTraversal() const {
	Post(root);
}

上面是一个简单的二叉树。先定义一个struct，把一个结点该有的东西写进去，要注意的是，我的定义里面并没有包含指向父结点的指针，只有指向左右孩子的指针，这种是双叉链表。某些情况下可能需要频繁调用父结点的数据，这个时候你可以写一个包含指向父结点的指针的结构体，变成一个三叉链表。
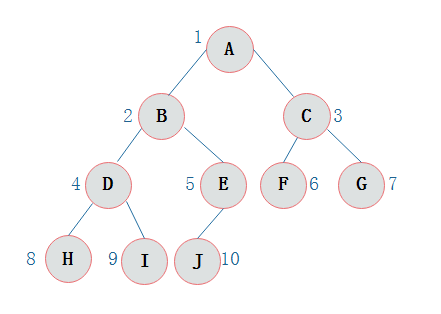
接下来就是一些常规的函数，插入啦、查找啦还有重要的三种遍历。下面解释遍历的时候都会用这个二叉树做说明：

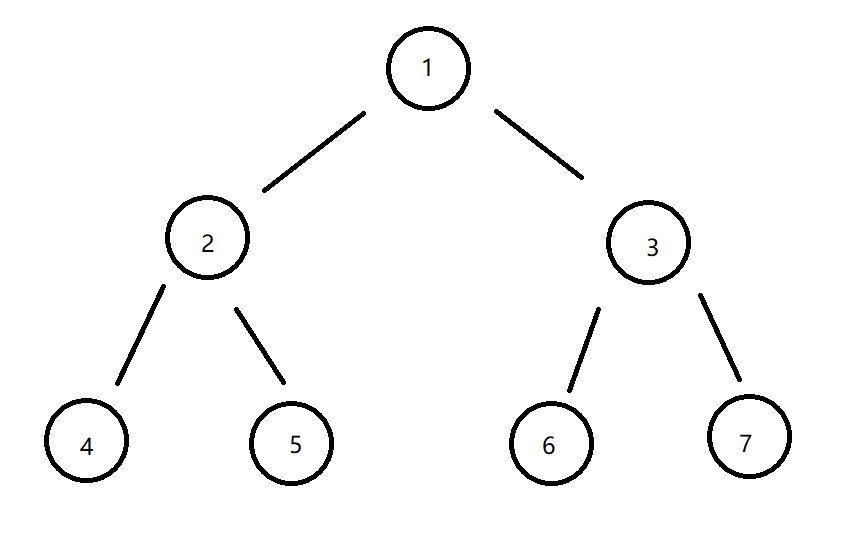
前序遍历是先访问根结点，再访问左子树，最后访问右子树。像上面这个二叉树，它最后会输出“1 2 4 5 3 6 7 ”，稍微看一下前序遍历的代码就看的出来。中序遍历则是先访问左子树，再访问根结点，最后访问右子树。同样是上面的二叉树，最后输出结果为“4 2 5 1 6 7 3 ”。后序遍历就是先访问左子树，再访问右子树，最后访问根结点，输出的结果为“4 5 2 6 7 3 1 ”。其实再认真看看三种遍历的算法，其实差别真的很小，就是cout放的位置不一样而已，但是这就意味着输出的时机不一样，三种遍历方法记起来也很容易。
其实除了这三种遍历，还有一种遍历叫做层次遍历，它是按二叉树的层次从小到大且每层从左到右的顺序一次访问结点，如果遍历上图的二叉树，输出的结果就是“1 2 3 4 5 6 7 ”。这种遍历我把它用在了插入的代码上，为了把二叉树插成完全二叉树，用层次遍历的方法按顺序插满。为了检验是否为完全二叉树，我们可以稍微测试一下：

很显然，跟上面说的结果一致，证明它确实是完全二叉树。
最后目光聚焦删除二叉树的代码，它其实就是用了后序遍历，不断的删除结点，最终把根结点删掉。关于遍历的应用还很多，留给读者自己摸索了。

堆(Heap)

堆是一类完全二叉树，它可以用于高效地实现排序、选择最大（小）值和优先队列。下面先聊一聊基本的定义和术语。
堆有两类，一类叫小顶堆（小根堆），一类叫大顶堆（大根堆）。若堆中所有非叶子结点均不大于其左右孩子结点，则称为小顶堆（小根堆）。大顶堆（大根堆）的定义可以读者自己推导一下。

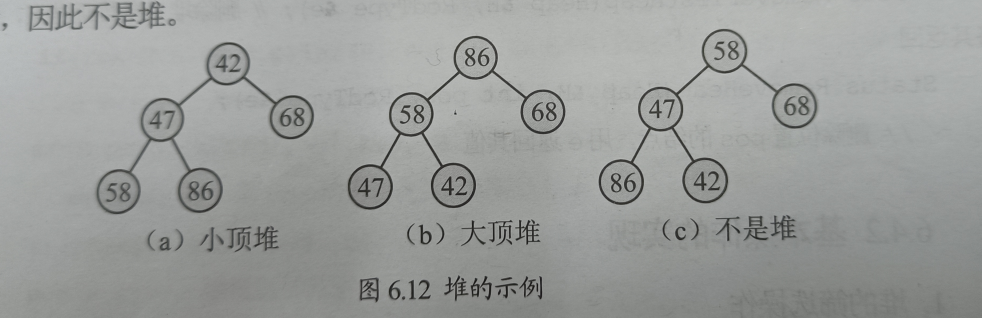
堆中根结点的位置称为堆顶，最后结点的位置称为堆尾，结点的个数称之为堆长度。堆很实用，因为它在每次添加或修改元素时，都可以自动调整自身的结构，使其重新成为一个大根堆或者小根堆。而且这个过程只要付出logN的代价（树的高度），在大样本的情况下优势非常大。

平时用堆的话一般就是用优先队列了，STL中有priority_queue容器去实现。

template <class T, class Container = vector,
class Compare = less > class priority_queue;

第一个参数是数据的类型，第二个参数是实现优先队列底层容器的类型，默认是vector，第三个参数是比较数据的方法，这个比较方法一般是重载了operator()的类，实现两个数据的比较。less实现的是大根堆，greater实现的是小根堆。如果元素的类型不是基本类型，那第三个参数一般需要自己重写一个比较函数的，不然less和greater不知道怎么去比较。
普通的队列是一种先进先出的数据结构，元素在队列尾追加，而从队列头删除。在优先队列中，元素被赋予优先级。当访问元素时，具有最高优先级的元素最先删除。优先队列具有最高级先出（First In Largest Out）的行为特征。
优先队列也是队，实现它的底层容器是vector，所以vector有的一些函数它都会有。
做一道LeetCode来介绍堆的优点：

class MedianFinder {
    priority_queue<int, vector<int>, less<int>> queMin;
	priority_queue<int, vector<int>, greater<int>> queMax;
public:
	MedianFinder() {}

	void addNum(int num) {
		if (queMin.empty() || num <= queMin.top()) {
			queMin.push(num);
			if (queMax.size() + 1 < queMin.size()) {
				queMax.push(queMin.top());
				queMin.pop();
			}
		}
		else {
			queMax.push(num);
			if (queMax.size() > queMin.size()) {
				queMin.push(queMax.top());
				queMax.pop();
			}
		}
	}

	double findMedian() {
		if (queMin.size() > queMax.size()) {
			return queMin.top();
		}
		return (queMin.top() + queMax.top()) / 2.0;
	}
};

这道题的题解很有趣，建了一个大根堆和一个小根堆，相当于两个金字塔塔尖相碰，中间的那个数就是中位数。

二叉查找树(Binary Search Tree)

二叉树的查找一般是通过遍历去实现，效率较低，因为元素的顺序没有规律。二叉查找树就是一种专门为查找而设计的树形数据结构，可以大大提高查找效率。
二叉查找树的定义：
若左子树非空，则左子树上所有的结点的值均小于根节点的值；
若右子树非空，则右子树上所有的结点的值均大于根结点的值；
左、右子树也分别是二叉查找树

其实二叉查找树的定义跟堆的定义挺像的，建议将两者比较着去记。由二叉查找树的定义可以得知，结点的值不允许重复，它的中序遍历是有序的。
下面实现自己定义的二叉查找树：

#pragma once
#include<iostream>

template<typename T>
struct BSTreeNode {
	T data;
	BSTreeNode<T>* leftChild, * rightChild;
	BSTreeNode() :data(NULL), leftChild(nullptr), rightChild(nullptr) {}
	BSTreeNode(T x) :data(x), leftChild(nullptr), rightChild(nullptr) {}
};

template<typename T>
class BinarySearchTree {
	BSTreeNode<T>* root;

	void DeleteTree(BSTreeNode<T>* head);
	void In(BSTreeNode<T>* head) const;
public:

	BinarySearchTree() :root(nullptr) {}
	BinarySearchTree(const T& data);
	~BinarySearchTree();

	bool BSTSearch(const T& target) const;
	void BSTInsert(const T& nodedata);
	void BSTRemove(const T& target);
	void InOrderPrint() const;
};

template<typename T>
void BinarySearchTree<T>::DeleteTree(BSTreeNode<T>* head) {
	if (head != nullptr) {
		DeleteTree(head->leftChild);
		DeleteTree(head->rightChild);
		delete head;
	}
}

template<typename T>
void BinarySearchTree<T>::In(BSTreeNode<T>* head) const {
	if (head != nullptr) {
		In(head->leftChild);
		std::cout << head->data << " ";
		In(head->rightChild);
	}
}

template<typename T>
BinarySearchTree<T>::BinarySearchTree(const T& data) {
	root = new BSTreeNode<T>(data);
}

template<typename T>
BinarySearchTree<T>::~BinarySearchTree() {
	DeleteTree(root);
}

template<typename T>
bool BinarySearchTree<T>::BSTSearch(const T& target) const {
	BSTreeNode<T>* node = root;
	while (node) {
		if (target < node->data) {
			node = node->leftChild;
		}
		else if (target > node->data) {
			node = node->rightChild;
		}
		else {
			break;
		}
	}
	if (node) {
		return true;
	}
	else {
		return false;
	}
}

template<typename T>
void BinarySearchTree<T>::BSTInsert(const T& nodedata) {
	if (!root) {
		root = new BSTreeNode<T>(nodedata);
		return;
	}

	BSTreeNode<T>* temp = nullptr;
	BSTreeNode<T>* current = root;
	while (current) {
		if (nodedata < current->data) {
			temp = current;
			current = current->leftChild;
			continue;
		}
		else if (nodedata > current->data) {
			temp = current;
			current = current->rightChild;
			continue;
		}
		else {
			break;
		}
	}
	if (!temp) {
		return;
	}

	current = new BSTreeNode<T>(nodedata);
	if (temp->data > current->data) {
		temp->leftChild = current;
	}
	else {
		temp->rightChild = current;
	}
}

template<typename T>
void BinarySearchTree<T>::BSTRemove(const T& target) {
	if (!root) {
		std::cout << "Root is empty. " << std::endl;
		return;
	}

	BSTreeNode<T>* tempParent = nullptr;
	BSTreeNode<T>* tempChild = root;
	while (tempChild) {
		if (target < tempChild->data) {
			tempParent = tempChild;
			tempChild = tempChild->leftChild;
			continue;
		}
		else if (target > tempChild->data) {
			tempParent = tempChild;
			tempChild = tempChild->rightChild;
			continue;
		}
		else {
			break;
		}
	}
	if (!tempChild) {
		std::cout << "Don't exist. " << std::endl;
		return;
	}

	if (tempChild->leftChild == nullptr && tempChild->rightChild == nullptr) {
		delete tempChild;
	}
	else if (tempChild->leftChild != nullptr && tempChild->rightChild == nullptr) {
		if (tempParent->leftChild == tempChild) {
			tempParent->leftChild = tempChild->leftChild;
			delete tempChild;
		}
		else {
			tempParent->rightChild = tempChild->leftChild;
			delete tempChild;
		}
	}
	else if (tempChild->leftChild == nullptr && tempChild->rightChild != nullptr) {
		if (tempParent->leftChild == tempChild) {
			tempParent->leftChild = tempChild->rightChild;
			delete tempChild;
		}
		else {
			tempParent->rightChild = tempChild->rightChild;
			delete tempChild;
		}
	}
	else {
		BSTreeNode<T>* temp = tempChild->rightChild;
		while (temp->rightChild) {
			temp = temp->rightChild;
		}
		if (tempParent->leftChild == tempChild) {
			tempParent->leftChild = temp;
			temp->rightChild = tempChild->rightChild;
			temp->leftChild = tempChild->leftChild;
			delete tempChild;
		}
		else {
			tempParent->rightChild = temp;
			temp->leftChild = tempChild->leftChild;
			temp->rightChild = tempChild->rightChild;
			delete tempChild;
		}
	}
	std::cout << "Done. " << std::endl;
}

template<typename T>
void BinarySearchTree<T>::InOrderPrint() const {
	In(root);
}

实现了一些基本的功能：查找、插入、移除、中序遍历，最后测试一下成果：

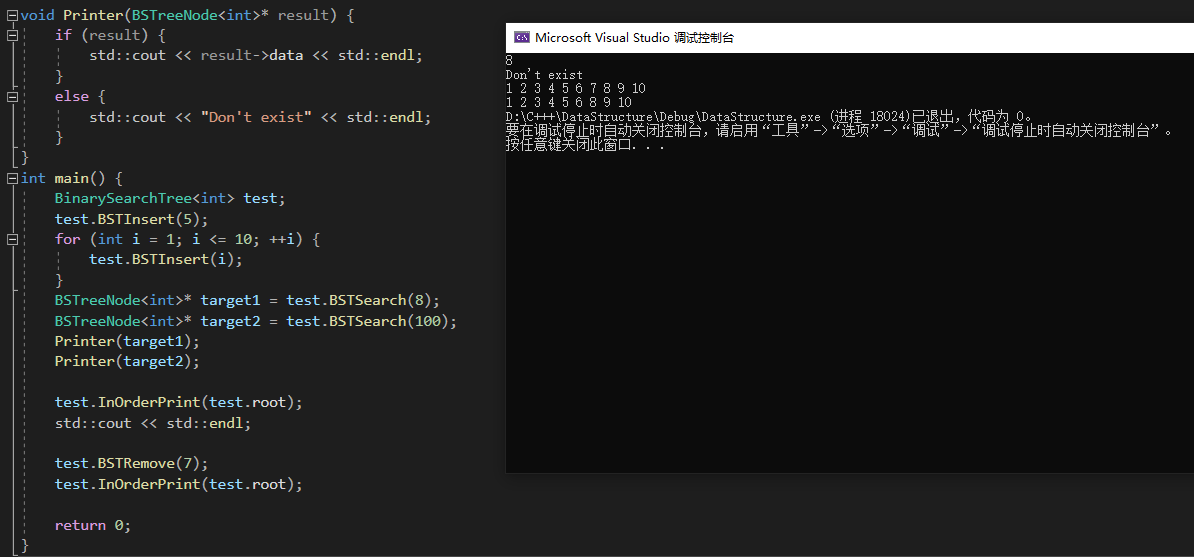
可以看出来中序遍历就是升序排序之后再输出的结果，这点非常好用。
另外需要注意的是移除操作，如果只是单纯删除目标结点，有可能导致删除后的二叉树不满足查找树的性质，所以为了解决这个问题，有两种做法：

在目标结点的左子树中找到最大值所在的结点补到被移除结点处
在目标结点的右子树中找到最小值所在的结点补到被移除结点处

两种方法都能保证删除后的二叉树依然满足查找树的性质，我用了第一种方法，就是在左子树中找最右的结点。还有一点要指出，在实现插入、移除功能的时候，频繁使用了父节点的数据，所以如果希望代码好看点，可以把树的结点设计成带父节点指针的三叉链表，方便读取父节点的信息。

平衡二叉树(Balanced Binary Sort Tree)

在写完查找树之后可以思考一下，怎样的查找树查找性能最优？答案是：树的高度应该为最小。满二叉树和完全二叉树的高度都是最小的，但是要在插入或者删除结点之后维持其高度最小的代价较大。平衡二叉查找树是一种可以兼顾查找和维护性能的折中方案。
平衡二叉查找树，简称平衡二叉树，它是具有以下性质的二叉树：

左子树和右子树的高度之差绝对值不超过1
它的左子树和右子树都是平衡二叉树

定义的第二条需要注意，平衡二叉树本身是二叉查找树。我们把左子树和右子树的高度之差定义为平衡因子（Balance Factor），按照平衡二叉树的定义，每个结点的平衡因子只可能为-1、0、1，只要有一个结点的平衡因子的绝对值大于1，那么这棵树就失去了平衡。
在平衡二叉树中插入一个新的结点后，从该结点起向上寻找第一个不平衡的结点（平衡因子变成了2或-2），以确定该树是否失衡。如果找到了，则以该结点为根的子树称为最小失衡树。如下图，在插入了49之后，以55为根结点的子树即为最小失衡树。

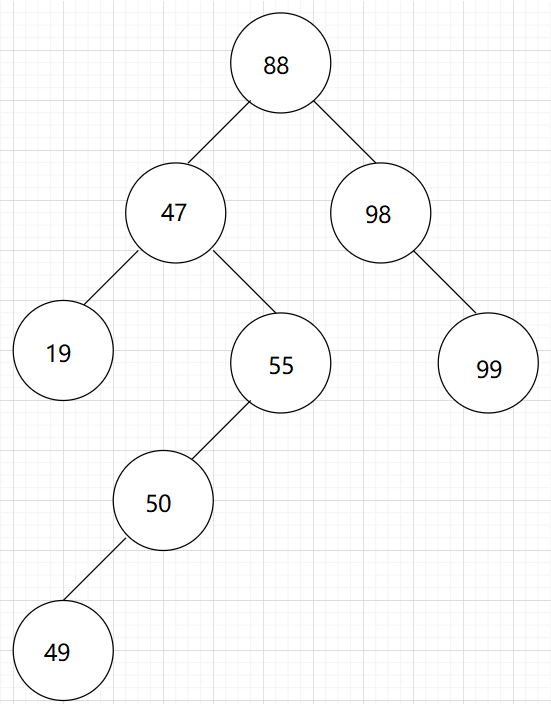
我们根据插入结点的位置，把最小失衡树分了四类：

LL型：在最小失衡树的左孩子的左子树上插入结点
RR型：在最小失衡树的右孩子的右子树上插入结点
LR型：在最小失衡树的左孩子的右子树上插入结点
RL型：在最小失衡树的右孩子的左子树上插入结点

对于简单的LL和RR型只需要一次右旋和左旋就能恢复平衡：

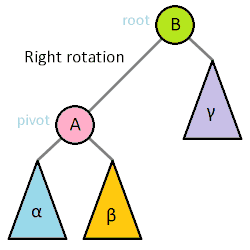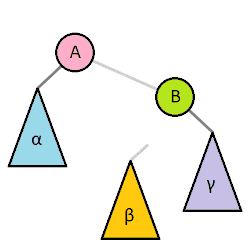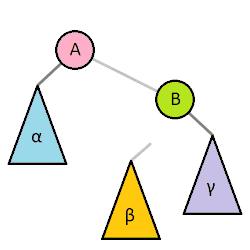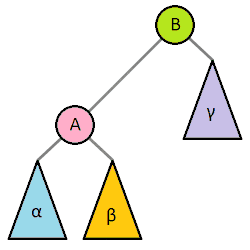
左旋和右旋

右旋是以最小失衡树的左孩子为轴（A结点），对根节点进行右旋（B结点），同时A结点的右子树会成为B结点的左子树。
左旋就是跟右旋相反的操作。它是以B结点为轴进行旋转，B结点的左子树会成为A结点的右子树。
简单的LL和RR型很好解决~~（其实也不是很好解决= =）~~，那对于复杂一点的LR和RL型其实就是需要两次旋转。对于LR型，可以先进行左旋，再进行右旋；对于RL型，则先进行右旋再进行左旋。实在找不到好的动图，大家自己画图理解一下吧。~~（摸了）~~
事实上平衡二叉树有很多种，最出名的是由前苏联数学家Adelse-Velskil和Landis在1962年提出的高度平衡二叉树，根据提出者的英文名字首写字母简称为AVL树。接下来我们实现一下平衡二叉树：

template <typename T>
struct AVLTreeNode {
	T data;
	int height;
	AVLTreeNode<T>* leftChild;
	AVLTreeNode<T>* rightChild;
	AVLTreeNode<T>(const T& theData) : data(theData), leftChild(nullptr), rightChild(nullptr), height(0) {}
};

template <typename T>
class AVLTree {
public:
	AVLTree<T>() :root(nullptr) {}
	~AVLTree<T>() {}

	void Insert(T nodedata);
	void DeleteNode(T nodedata);
	void Search(T& nodedata);
	void InorderPrinter();

private:
	AVLTreeNode<T>* root;

	void Add(AVLTreeNode<T>*& t, T& x);					//插入的内部接口
	bool Delete(AVLTreeNode<T>*& t, T& x);				//删除的内部接口
	bool Find(AVLTreeNode<T>* t, const T& x) const;		//查找的内部接口
	void InorderTraversal(AVLTreeNode<T>* t);			//中序遍历的内部接口
	AVLTreeNode<T>* FindMin(AVLTreeNode<T>* t) const;	//查找最小值结点
	AVLTreeNode<T>* FindMax(AVLTreeNode<T>* t) const;	//查找最大值结点
	int GetHeight(AVLTreeNode<T>* t);					//求树的高度
	AVLTreeNode<T>* LL_Rotate(AVLTreeNode<T>* t);		//左旋
	AVLTreeNode<T>* RR_Rotate(AVLTreeNode<T>* t);		//右旋
	AVLTreeNode<T>* LR_Rotate(AVLTreeNode<T>* t);		//双旋，右左
	AVLTreeNode<T>* RL_Rotate(AVLTreeNode<T>* t);		//双旋，左右
};

template<typename T>
void AVLTree<T>::Insert(T nodedata) {
	Add(root, nodedata);
}

template<typename T>
void AVLTree<T>::DeleteNode(T nodedata) {
	Delete(root, nodedata);
}

template<typename T>
void AVLTree<T>::Search(T& nodedata) {
	Find(root, nodedata);
}

template<typename T>
void AVLTree<T>::InorderPrinter() {
	InorderTraversal(root);
}

template <typename T>
void AVLTree<T>::Add(AVLTreeNode<T>*& t, T& x) {
	if (!t) {
		t = new AVLTreeNode<T>(x);
	}
	else if (x < t->data) {
		Add(t->leftChild, x);
		if (GetHeight(t->leftChild) - GetHeight(t->rightChild) > 1) {
			if (x < t->leftChild->data) {
				t = LL_Rotate(t);
			}
			else {
				t = LR_Rotate(t);
			}
		}
	}
	else if (x > t->data) {
		Add(t->rightChild, x);
		if (GetHeight(t->rightChild) - GetHeight(t->leftChild) > 1) {
			if (x > t->rightChild->data) {
				t = RR_Rotate(t);
			}
			else {
				t = RL_Rotate(t);
			}
		}
	}
	else {

	}
	t->height = std::max(GetHeight(t->leftChild), GetHeight(t->rightChild)) + 1;
}

template <typename T>
bool AVLTree<T>::Delete(AVLTreeNode<T>*& t, T& x) {
	if (t == nullptr) {
		return false;
	}
	else if (t->data == x) {
		if (t->leftChild != nullptr && t->rightChild != nullptr) {
			if (GetHeight(t->leftChild) > GetHeight(t->rightChild)) {
				t->data = FindMax(t->leftChild)->data;
				Delete(t->leftChild, t->data);
			}
			else {
				t->data = FindMin(t->rightChild)->data;
				Delete(t->rightChild, t->data);
			}
		}
		else {
			AVLTreeNode<T>* old = t;
			t = t->leftChild ? t->leftChild : t->rightChild;
			delete old;
		}
	}
	else if (x < t->data) {
		Delete(t->leftChild, x);
		if (GetHeight(t->rightChild) - GetHeight(t->leftChild) > 1) {
			if (GetHeight(t->rightChild->leftChild) > GetHeight(t->rightChild->rightChild)) {
				t = RL_Rotate(t);
			}
			else {
				t = RR_Rotate(t);
			}
		}
		else {
			t->height = std::max(GetHeight(t->leftChild), GetHeight(t->rightChild)) + 1;
		}
	}
	else {
		Delete(t->rightChild, x);
		if (GetHeight(t->leftChild) - GetHeight(t->rightChild) > 1) {
			if (GetHeight(t->leftChild->rightChild) > GetHeight(t->leftChild->leftChild)) {
				t = LR_Rotate(t);
			}
			else {
				t = LL_Rotate(t);
			}
		}
		else {
			t->height = std::max(GetHeight(t->leftChild), GetHeight(t->rightChild)) + 1;
		}
	}
	return true;
}

template <typename T>
bool AVLTree<T>::Find(AVLTreeNode<T>* t, const T& x) const {
	if (t == nullptr) {
		return false;
	}
	if (x < t->data) {
		return Find(t->leftChild, x);
	}
	else if (x > t->data) {
		return Find(t->rightChild, x);
	}
	else {
		return true;
	}
}

template <typename T>
void AVLTree<T>::InorderTraversal(AVLTreeNode<T>* t) {
	if (t) {
		InorderTraversal(t->leftChild);
		std::cout << t->data << ' ';
		InorderTraversal(t->rightChild);
	}
}

template <typename T>
AVLTreeNode<T>* AVLTree<T>::FindMax(AVLTreeNode<T>* t) const {
	if (t == nullptr) {
		return nullptr;
	}
	if (t->rightChild == nullptr) {
		return t;
	}
	return FindMax(t->rightChild);
}

template <typename T>
AVLTreeNode<T>* AVLTree<T>::FindMin(AVLTreeNode<T>* t) const {
	if (t == nullptr) {
		return nullptr;
	}
	if (t->leftChild == nullptr) {
		return t;
	}
	return FindMin(t->leftChild);
}

template <typename T>
int AVLTree<T>::GetHeight(AVLTreeNode<T>* t) {
	if (t == nullptr) {
		return -1;
	}
	else {
		return t->height;
	}
}

template <typename T>
AVLTreeNode<T>* AVLTree<T>::LL_Rotate(AVLTreeNode<T>* t) {
	AVLTreeNode<T>* q = t->leftChild;
	t->leftChild = q->rightChild;
	q->rightChild = t;
	t = q;
	t->height = std::max(GetHeight(t->leftChild), GetHeight(t->rightChild)) + 1;
	q->height = std::max(GetHeight(q->leftChild), GetHeight(q->rightChild)) + 1;
	return q;
}

template <typename T>
AVLTreeNode<T>* AVLTree<T>::RR_Rotate(AVLTreeNode<T>* t) {
	AVLTreeNode<T>* q = t->rightChild;
	t->rightChild = q->leftChild;
	q->leftChild = t;
	t = q;
	t->height = std::max(GetHeight(t->leftChild), GetHeight(t->rightChild)) + 1;
	q->height = std::max(GetHeight(q->leftChild), GetHeight(q->rightChild)) + 1;
	return q;
}

template <typename T>
AVLTreeNode<T>* AVLTree<T>::LR_Rotate(AVLTreeNode<T>* t) {
	AVLTreeNode<int>* q = RR_Rotate(t->leftChild);
	t->leftChild = q;
	return LL_Rotate(t);
}

template <typename T>
AVLTreeNode<T>* AVLTree<T>::RL_Rotate(AVLTreeNode<T>* t) {
	AVLTreeNode<int>* q = RR_Rotate(t->rightChild);
	t->rightChild = q;
	return RR_Rotate(t);
}

上面简单实现了一下AVL树的一些基本操作，旋转和删除结点操作是我个人认为最难实现的部分，建议画图去辅助理解，同时还能对比查找树的做法，因为平衡树也是一种查找树，他们二者肯定是有很多相似之处的。
最后写一个例子测试一下：

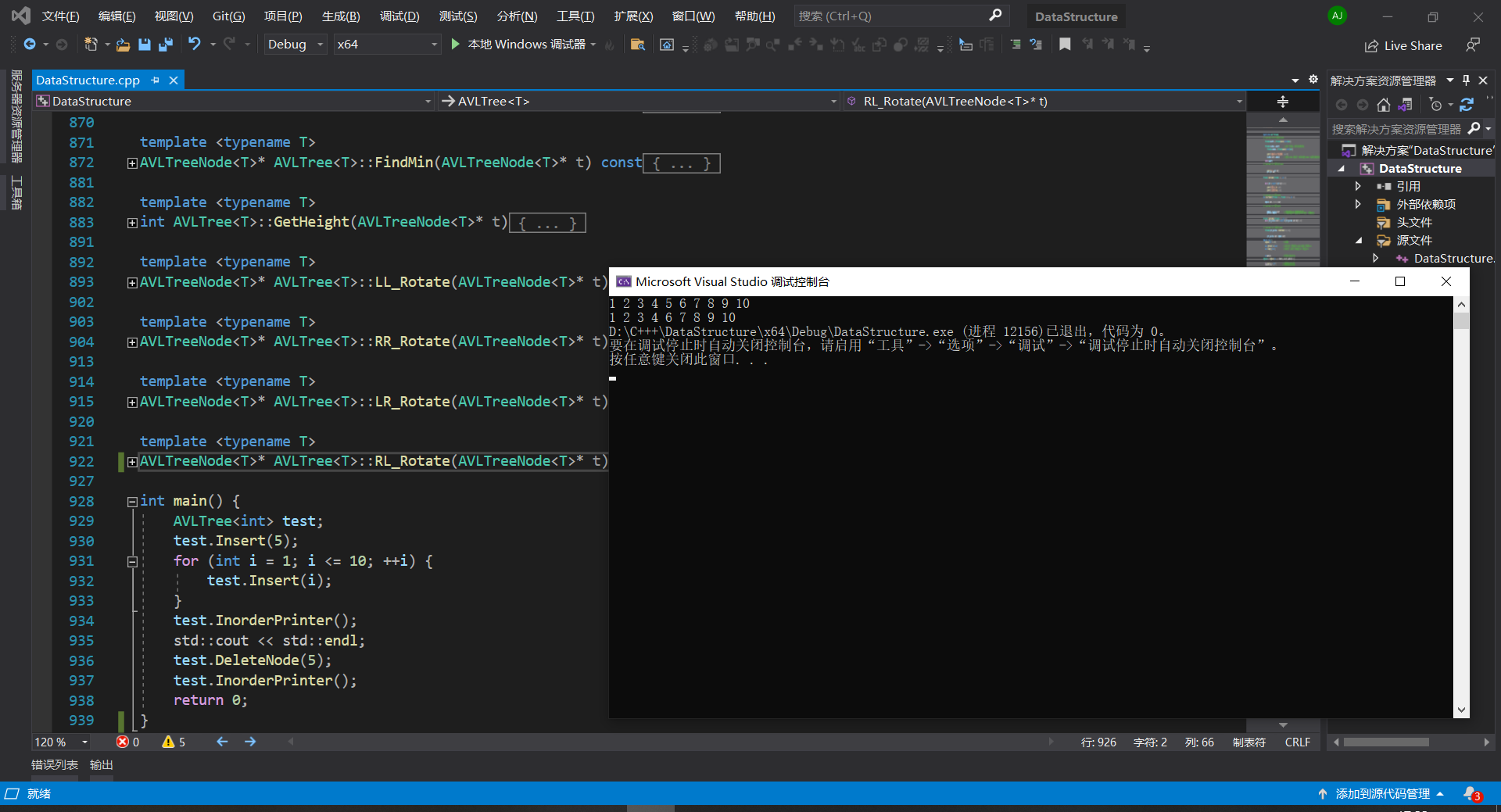
中序遍历还是有序的输出，符合我们的要求。

图（Graph）

图形结构是一种比树形结构更复杂的非线性数据结构，而且概念也特别多，下面一点点地来了解它。

基本术语

在图中，将数据元素称为顶点（Vertex），顶点之间的关系称为边（Edge），图由有限顶点集V和有限边集E组成，记为：G=(V, E)，其中顶点总数记为n，边的总数记为e。
为了解释方便，用一张图来形容有向图和无向图：

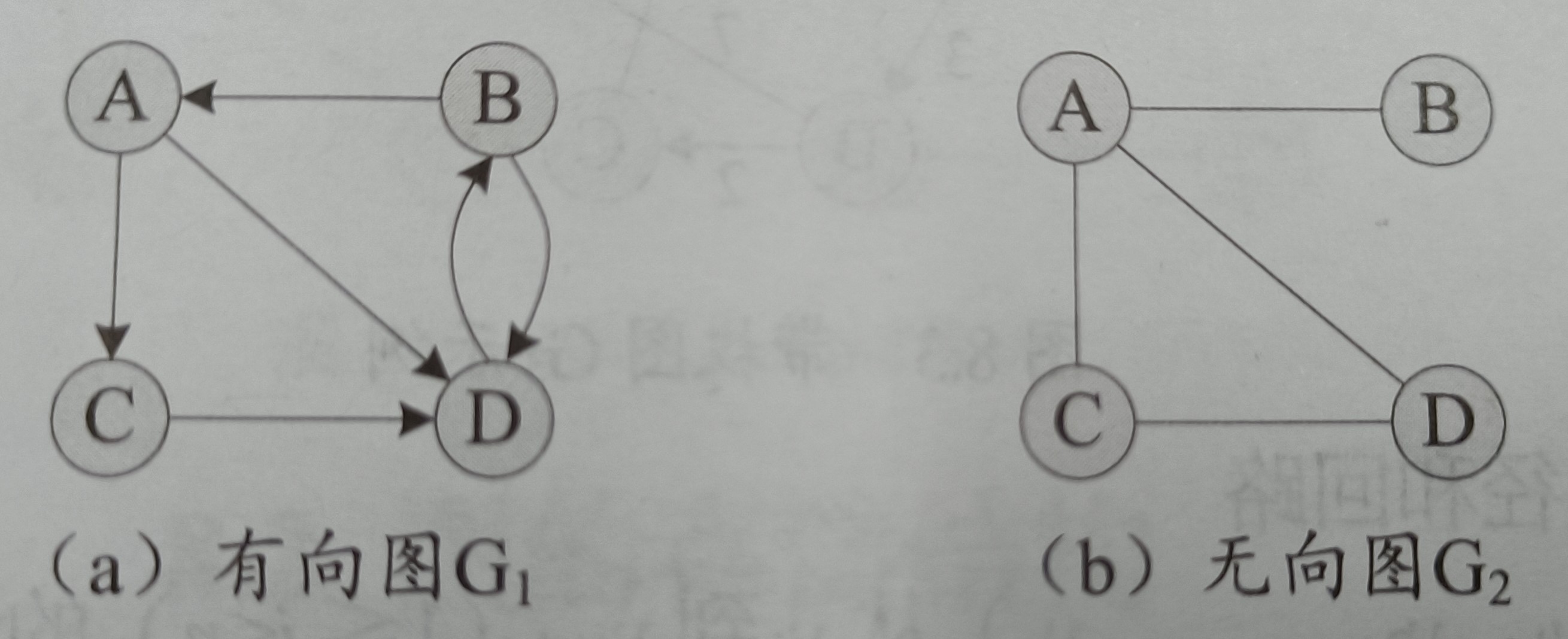
有向图的边是带方向的，只能按照箭头的方向去访问其他顶点。有向图的边称为有向边，或者弧（Arc）。无向图的边则没有方向性，称为无向边，简称边，两顶点间可以相互访问。
假设两个图G=(V, E)和G'=(V', E')，如果V'⊆V且E'⊆E，则称G'为G的子图。说人话就是在G中切割一部分出来，不改变边的方向，那切割的那些部分都是G的子图。
包含所有可能的边的图称为完全图。无向完全图包含n (n - 1) / 2条边，有向完全图包含n (n - 1)条弧。说人话就是把所有顶点之间都牵条线，无向图就变无向完全图了。对于有向图就要考虑方向性，除了“过去”还要“回来”，所以每个顶点之间牵两条线，就这么简单。
在图中，顶点的度（Degree）是指依附于该顶点的边数。无向图中就看顶点有多少条边就行了。对于有向图，还要区分入度（InDegree）和出度（OutDegree），入度是指该顶点为终点的弧的数目，出度是指以该顶点为起点的弧的数目，有向图顶点的度是出度和入度之和。
有时候，边或弧需要附加一些属性信息，比如两个顶点之间的距离、旅行时间或者某种代价等，通常称此信息为权（Weight），带权的图又称为带权图，或简称为网（Network）。
如果从顶点A₁到顶点Aₙ的边（弧）都存在，则称存在从顶点A₁到顶点Aₙ的长度为n - 1的路径。如果路径上顶点都不同，则称这个路径为简单路径。路径长度是指路径包含的边数。如果一条路径从某个顶点出发，最终连接到它自身，则称此路径为回路。
在无向图中，如果顶点A₁到顶点Aₙ有路径，则称A₁和Aₙ是连通的。如果图中任意两个顶点都是连通的，则称此图为连通图（Connected Graph）。在有向图中，如果顶点A₁到顶点Aₙ有路径，顶点Aₙ到顶点A₁也有路径，则称A₁和Aₙ是连通的。如果图中任意两个顶点都是连通的，则称此图为强连通图（Strong Connected Graph）。
连通图的生成树（Spanning Tree）是含有所有顶点且只有n - 1条边的连通子图。首先，它包含了所有的顶点；齐次，它只有n - 1条边；最后，它是子图。这三点很重要，不要看到有n - 1条边就说这是生产树。

邻接矩阵和邻接表

图这么复杂，我们要怎么去存它呢？基于多对多这一性质，我们可以设计一种叫邻接矩阵（Adjacency Matrix）和邻接表（Adjacency List）的结构去储存它，下面是两种结构的示意图：

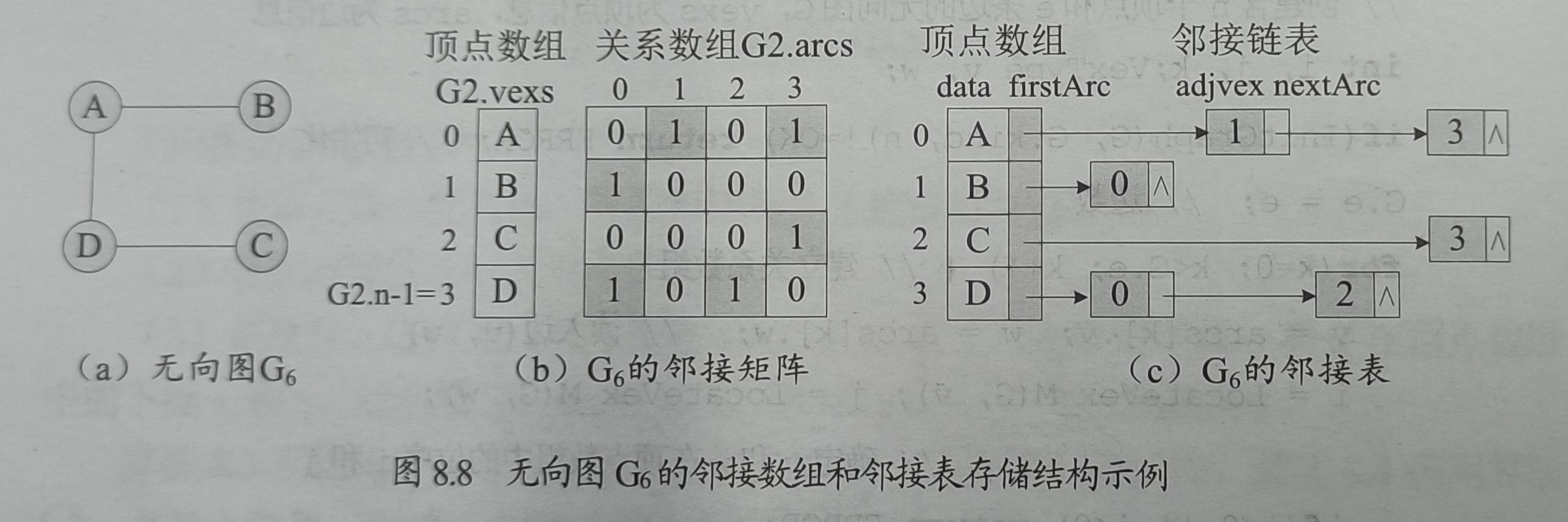
两种结构都有一个顶点数组，用来存放顶点的一些信息，比如名字、顺序等。邻接矩阵的关系数组是存边的信息，它是一个二维数组，如果存在顶点V[i]到V[j]的边，关系数组的A[i][j]就等于1，如果没有，就等于0，对于网还可以存权。容易得出，左上到右下的对角线自然全是0，因为自己不用跟自己连线。而邻接表就更直观了，用了单链表的方法，把相邻的顶点接在一起。对于有向图和无向图，两者的实现上有是区别的，这也导致两者在性能上有所不同。当图的边数很少时（即稀疏图），关系数组含有大量0，浪费了大量内存。在存储稀疏图的时候会更常用邻接表。
在设计上，邻接矩阵本质上就是矩阵，所以可以用一个二维数组去存。对于邻接表，本质上是若干链表组成的，所以可以用一个数组去存每个链表的头节点。

图的遍历

图的遍历有两种：广度优先遍历和深度优先遍历，又叫广度优先搜索（BFS）和深度优先搜索（DFS）。其实对于深度优先遍历，我们在二叉树那一块用的比较多了，前、中、后序遍历的思想都是深度优先遍历：一条路走到底。对于广度优先遍历，其实二叉树的层次遍历就是这样的思想：把邻接的、尚未访问过的节点都访问一遍。对于两种遍历我通过两道LeetCode来说明。

深度优先搜索

首先是深度优先搜索：

class Solution {
public:
	vector<vector<int>> result;
	vector<int> temp;
	void dfs(vector<vector<int>>& graph, int x, int n) {
		if (x == n) {
			result.push_back(temp);
			return;
		}
		for (auto& y : graph[x]) {
			temp.push_back(y);
			dfs(graph, y, n);
			temp.pop_back();
		}
	}
	vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
		temp.push_back(0);
		dfs(graph, 0, graph.size() - 1);
		return result;
	}
};

题目中的有向无环图（Directed Acyclic Graph）是指不存在回路的有向图。对于搜索路径，我们可以从起点出发，顺着任意路径探索到达终点的路径，如果找到了，就将路径保存到数组中。由于这是一个有向无环图，所以不用担心会原地转圈。这里的搜索路径是沿着一条路走到底的，符合DFS的思想。

广度优先搜索

同意是上面的题目，我也可以用广度优先搜索：

class Solution {
public:
    vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
        queue<vector<int>> que;
        que.push({0});

        while (!que.empty()) {
            auto path = que.front();
            que.pop();

            auto cur = path.back();
            for (auto& next : graph[cur]) {
                path.push_back(next);

                if (next == (int)graph.size() - 1) {
                    ans.push_back(path);
                }
                else {
                    que.push(path);
                }

                path.pop_back();
            }
        }

        return ans;
    }

private:
    vector<vector<int>> ans;
};

我用的是DFS，BFS是在题解里面找的。道理也很简单，用一个队列存图，然后暴力遍历，直到找到目的地。

结语

断断续续写了两个月，有懒的原因，也有学习上的原因。这学期的课超多作业，每周都要写40道大题，传热学和工程热力学简直要我命= =。另外腾讯的UE公开课也占用了我不少时间，最近也开始学UE了，时间完全不够用。我知道最后的图论介绍太少了，一些经典算法没有展示。但是我想这只是对数据结构的基本介绍，感兴趣的可以自己的往深学，比如我现在还没写出来的Dijkstra算法。另外平衡树之前的代码有点臭，但是有点懒得改了。总之，这篇博客暂时先这样了，后面可能会慢慢更新，再说吧。

posted @ 2021-11-13 17:31 Jay_Auditore 阅读(231) 评论(3) 编辑收藏举报

刷新页面返回顶部

Jay_Auditore

You can't fool me with your crocodile tears.