20182305 2019-2020-1 《数据结构与面向对象程序设计》实验九报告

20182305 2019-2020-1 《数据结构与面向对象程序设计》实验八报告

课程：《程序设计与数据结构》
班级： 1823
姓名： 孙铭泽
学号：20182305 
实验教师：王志强
实验日期：2019年12月2日
必修/选修： 必修

1.实验内容

• (1) 初始化：根据屏幕提示（例如：输入1为无向图，输入2为有向图）初始化无向图和有向图（可用邻接矩阵，也可用邻接表），图需要自己定义（顶点个数、边个数，建议先在草稿纸上画出图，然后再输入顶点和边数）（2分）

• (2) 图的遍历：完成有向图和无向图的遍历（深度和广度优先遍历）（4分）

• (3) 完成有向图的拓扑排序，并输出拓扑排序序列或者输出该图存在环（3分）

• (4) 完成无向图的最小生成树（Prim算法或Kruscal算法均可），并输出（3分）

• (5) 完成有向图的单源最短路径求解（迪杰斯特拉算法）（3分）

2. 实验过程及结果

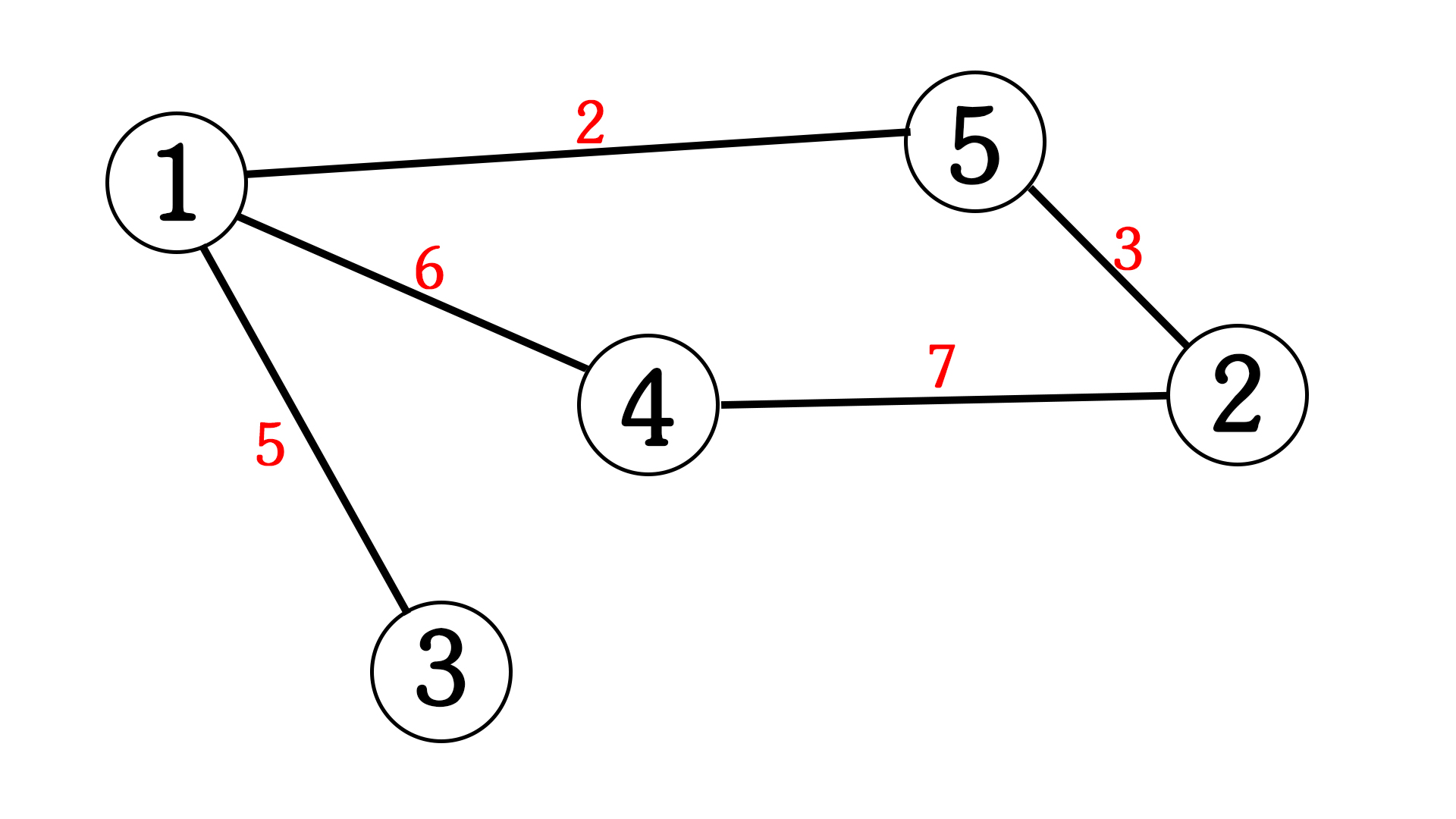
• 按照实验要求进行每一步的操作。
  初始化图

 public void create()
    {
        System.out.print("请输入结点数:");
        vexnum = input.nextInt();
        vexs = new char[vexnum]; // vexnum长度的顶点数组
        isVisited = new int[vexnum];
        System.out.print("请输入边数:");
        arcnum = input.nextInt();
        adjMatrix = new int[vexnum][vexnum];
        //构建顶点数组
        System.out.println("请依次输入顶点：");

        for(int i=0;i<vexnum;i++)
        {
            vexs[i] = input.next().charAt(0);
        }

        //初始化邻接矩阵
        for(int i=0;i<vexnum;i++)
            for(int j=0;j<vexnum;j++)
                adjMatrix[i][j]=0;

        int i = 0;
        int vexA, vexB;
        while (i < arcnum) {
            System.out.println("请输入相连接的结点");
            vexA = input.nextInt();
            while (vexA < 1 || vexA > vexnum)
            {
                System.out.println("范围不符合，请重新输入：");
                vexA = input.nextInt();
            }
            vexB = input.nextInt();
            while (vexB < 1 || vexB > vexnum)
            {
                System.out.println("范围不符合，请重新输入：");
                vexB = input.nextInt();
            }
            adjMatrix[vexA - 1][vexB - 1] = 1;
            adjMatrix[vexB - 1][vexA - 1] = 1;

            if (i == arcnum - 1)
            {
                System.out.println("Ending!");
            }
            else
            {
                System.out.println("Continue!");
            }
            i++;
        }
    }
![](https://img2018.cnblogs.com/blog/1780041/201912/1780041-20191208152413735-451025846.png)

对图进行遍历操作

    public void DFS(int i)
    {
        isVisited[i]=1;
        System.out.print(vexs[i]);
        for(int j=0;j<vexnum;j++){
            if(adjMatrix[i][j]==1&&isVisited[j]==0)
            {
                System.out.print("—>");
                DFS(j);
            }
        }

    }

public void BFS()
    {
        char temp=(char)list.poll();
        int x=temp-'0'; // 转换为数字
        isVisited[x-1]=1;
        System.out.print(temp);
        List nerborpointlist=getCurrent(x-1);
        for(int i=0;i<nerborpointlist.size();i++){
            char j=(char)nerborpointlist.get(i);
            list.add(j);
            int k=j-'0';
            isVisited[k-1]=1;
        }
        if(!list.isEmpty()){
            System.out.print("—>");
            BFS();
        }
    }

prim算法：

 public void prim( float[][] weight) {  //num为顶点数，weight为权
        float[] lowcost = new float[vexnum + 1];  //到新集合的最小权
        int[] closest = new int[vexnum + 1];  //代表与s集合相连的最小权边的点

        boolean[] s = new boolean[vexnum + 1];  //s[i] == true代表i点在s集合中

        s[1] = true;  //将第一个点放入s集合

        for(int i = 2; i <= vexnum; i++) {  //初始化辅助数组
            lowcost[i] = weight[1][i];
            closest[i] = 1;
            s[i] = false;
        }
        for(int i = 1; i < vexnum; i++) {
            float min = Float.MAX_VALUE;
            int j = 1;
            for(int k = 2; k <= vexnum; k++) {
                if((lowcost[k] < min) && (!s[k])) {//根据最小权加入新点
                    min = lowcost[k];
                    j = k;
                }
            }

            System.out.println("加入点" + j + ". " + j + "---" + closest[j]);//新加入点的j和与j相连的点

            s[j] = true;//加入新点j

            for(int k = 2; k <= vexnum; k++) {
                if((weight[j][k] < lowcost[k]) && !s[k]) {//根据新加入的点j,求得最小权
                    lowcost[k] = weight[j][k];
                    closest[k] = j;
                }
            }
        }
    }

最小生成树加入结点的顺序图

3. 实验过程中遇到的问题和解决过程

• 问题一：输入结点时遇到空指针异常的抛出。
  
• 问题一解决办法：检查代码后发现是vexs[i] = input.next().charAt(0); 这条语句使用前没有初始化定义vexs[]数组的长度，导致这样的错误。加上 vexs = new char[vexnum]; // vexnum长度的顶点数组 语句解决问题。后面的isVisited[]数组用来判断是否访问过的数组也遇上了同样的问题，同样方法解决。
• 问题二：实验过程中对图各个边的权值进行赋值的操作问题
• 问题二解决办法：选择使用二维数组，并将0行和0列设置为0，不使用。便于后面程序编写时的理解，给自己减少负担。这个二维数组需要自己手动写好在代码里，其实是固定死自己的图的样子其他样式的图就没法用。这个问题我还真不知道该怎么解决。
• 问题三：输入时有些麻烦。尤其是对边进行输入时（确定哪些结点是相连的）
• 问题三解决办法：如果输入错误，就要将程序重新开始，重新进行之前的所有步骤，很麻烦。我在写这个代码时候，加入了一些循环和判断，来避免出现输入错误导致程序直接结束。增加容错率。但是有一些关键步骤，比如确定边，没办法用程序进行修正，还是需要在输入时小心。其实自己有一些设想，但是不知道怎么实现。实现起来有一些麻烦。

其他（感悟、思考等）

这次的实验是将之前学过的许多内容进行结合和综合运用，难度并不是很大，但是需要细细思考和耐心理解。不然还有很多地方容易出错。