跳表:Redis中如何实现有序集合?(Leetcode 1206)










练习: 设计跳表
不使用任何库函数,设计一个跳表。
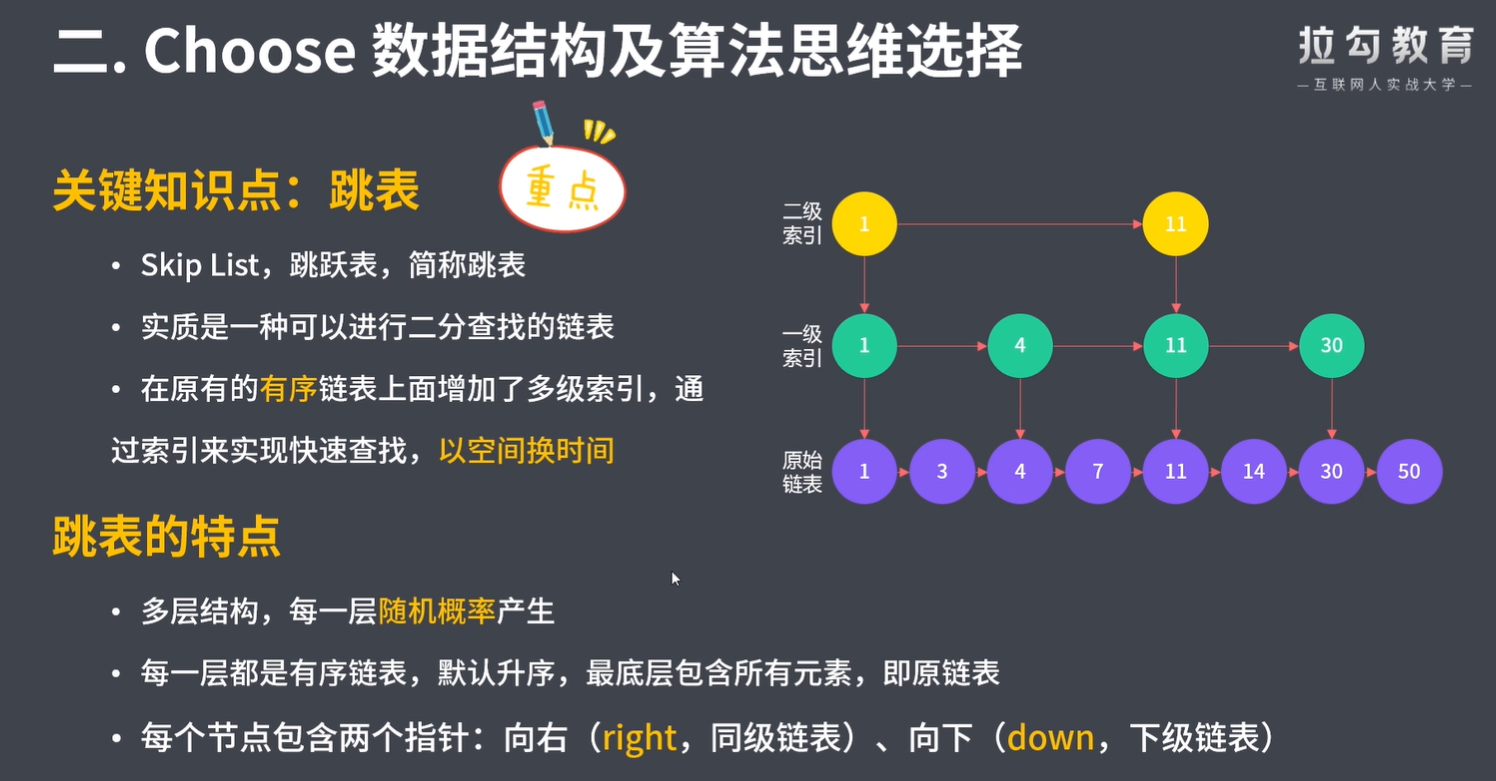
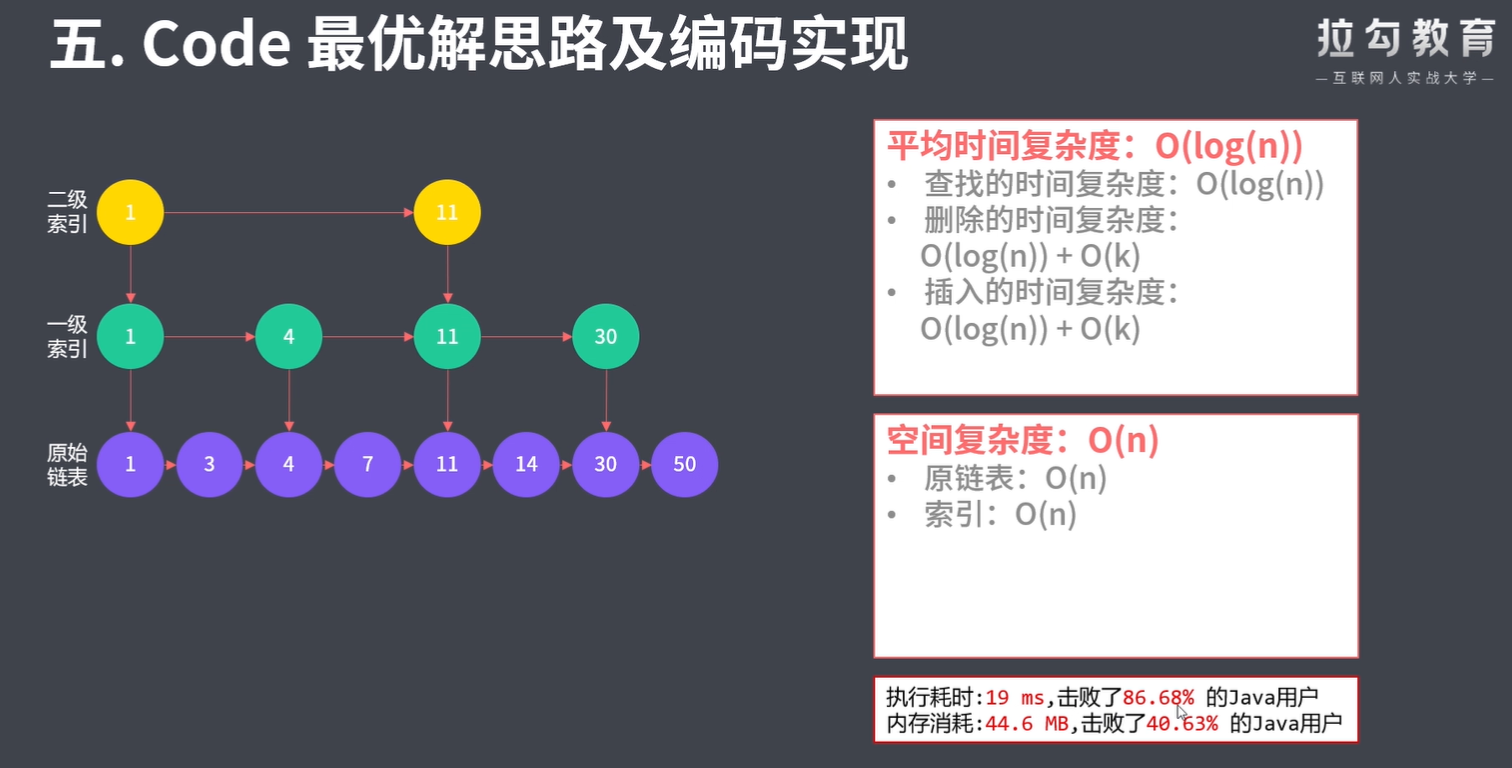
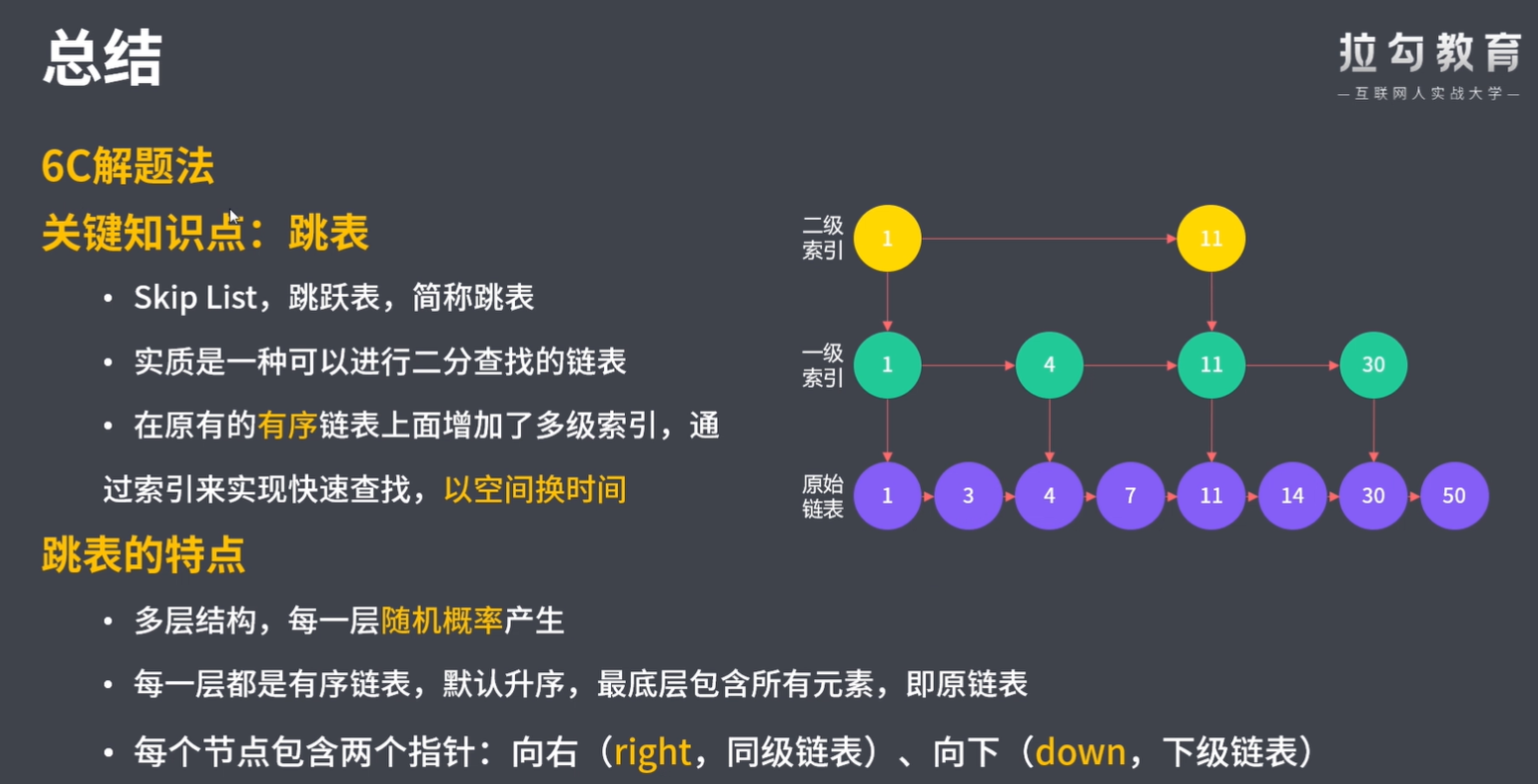
跳表是在 O(log(n)) 时间内完成增加、删除、搜索操作的数据结构。跳表相比于树堆与红黑树,其功能与性能相当,并且跳表的代码长度相较下更短,其设计思想与链表相似。
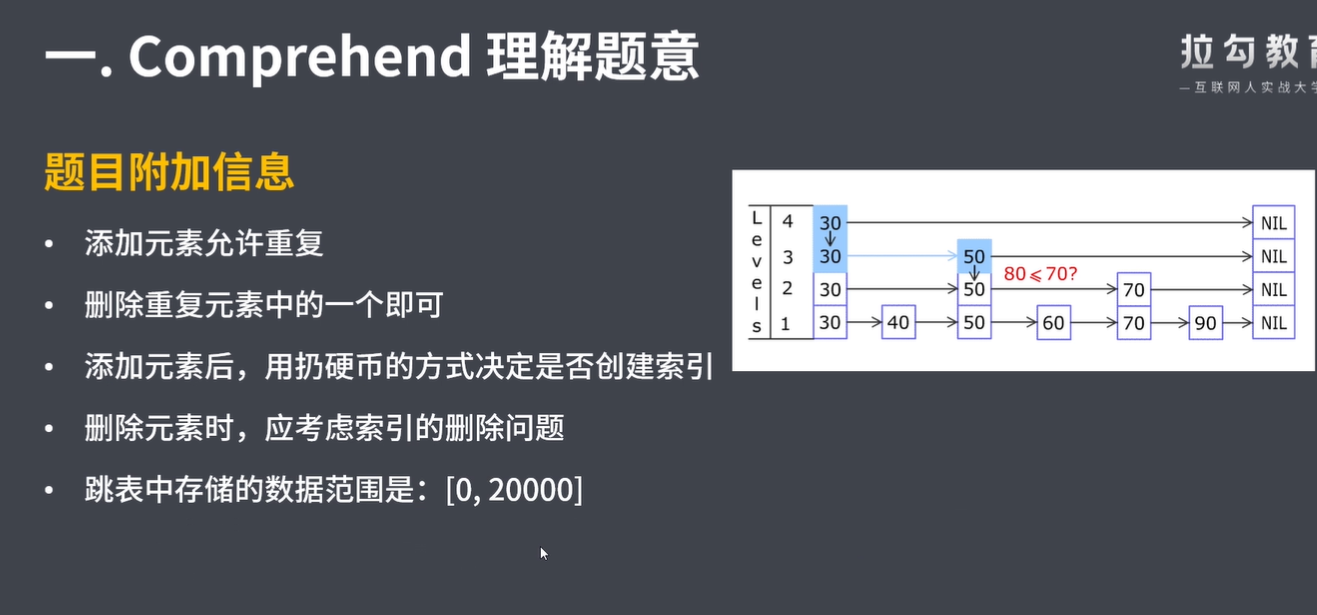
例如,一个跳表包含 [30, 40, 50, 60, 70, 90],然后增加 80、45 到跳表中,以下图的方式操作:
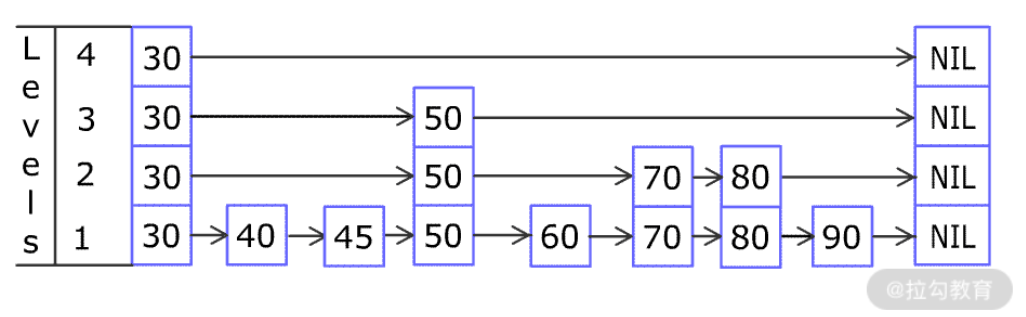
跳表中有很多层,每一层是一个短的链表。在第一层的作用下,增加、删除和搜索操作的时间复杂度不超过 O(n)。跳表的每一个操作的平均时间复杂度是 O(log(n)),空间复杂度是 O(n)。
在本题中,你的设计应该要包含这些函数:
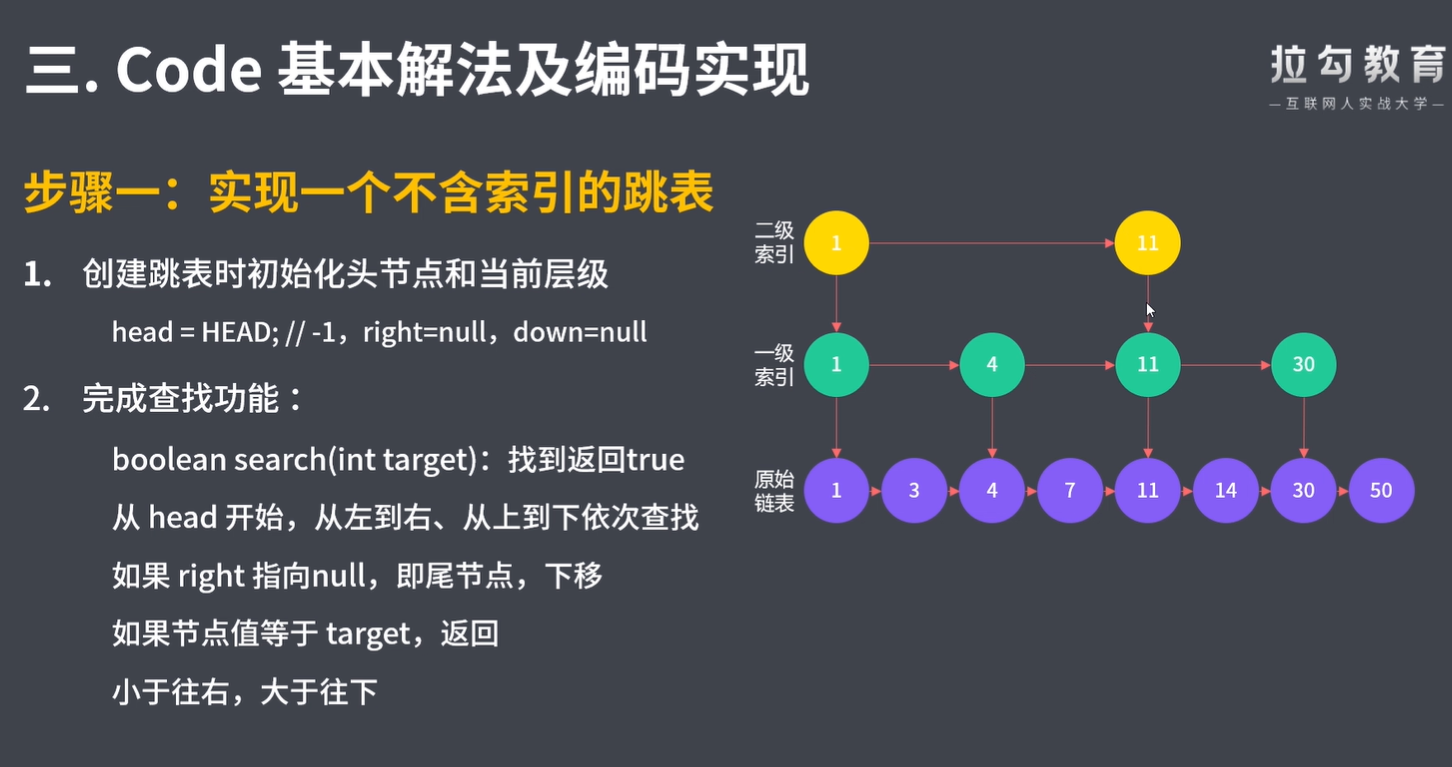
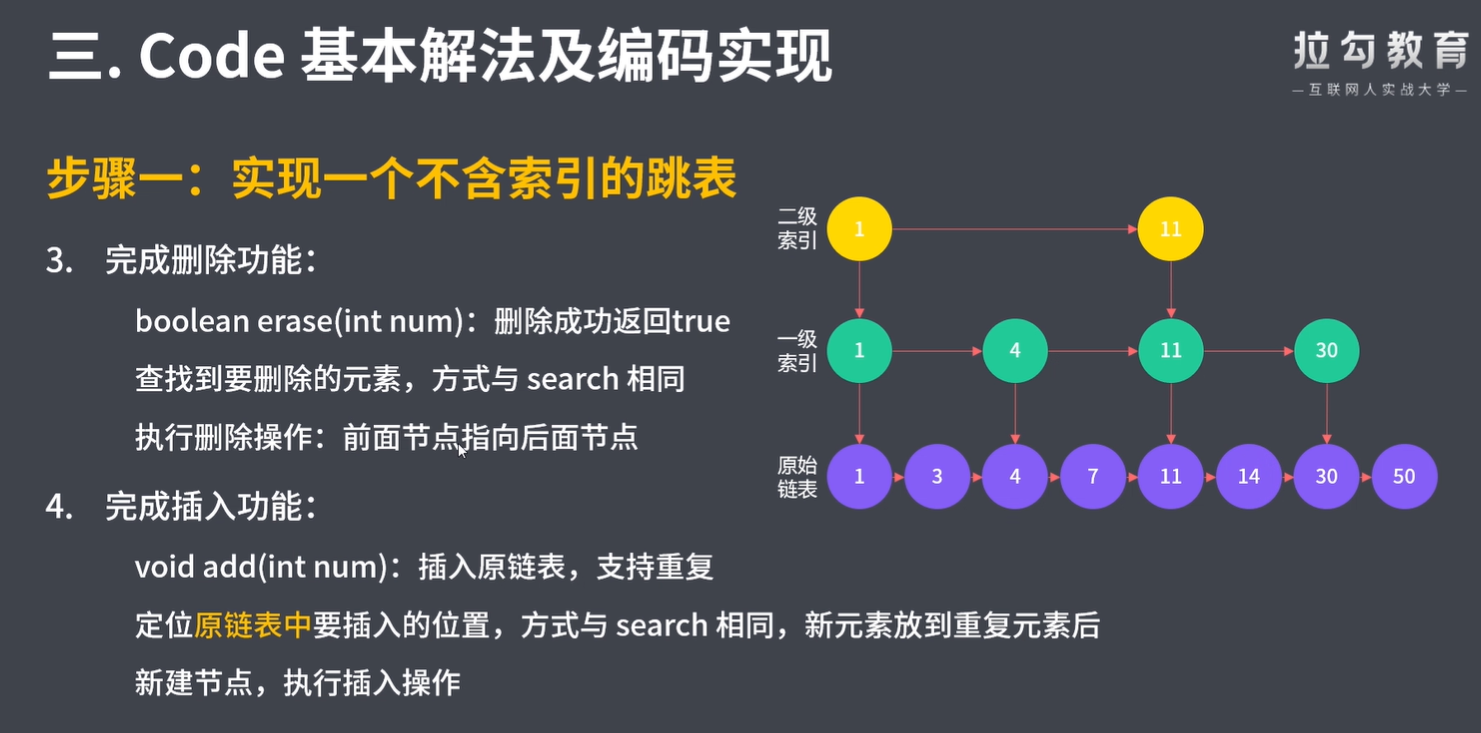
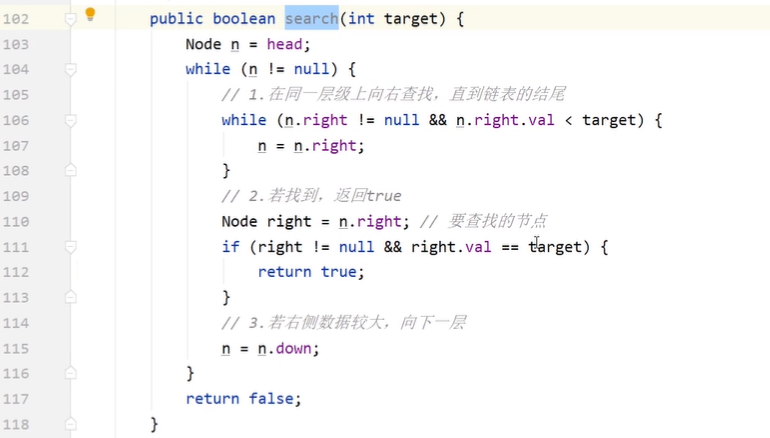
bool search(int target) : 返回target是否存在于跳表中。
void add(int num): 插入一个元素到跳表。
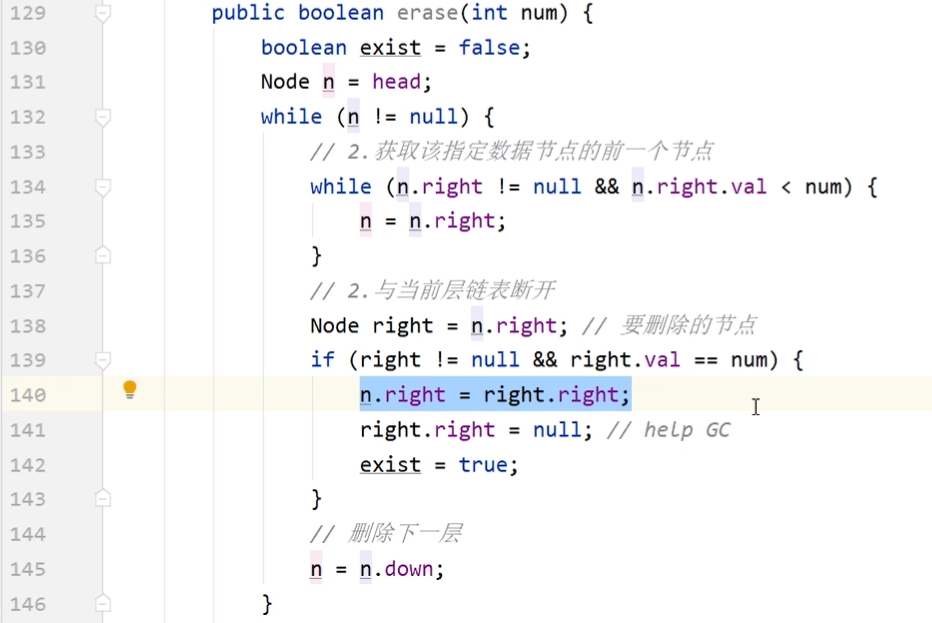
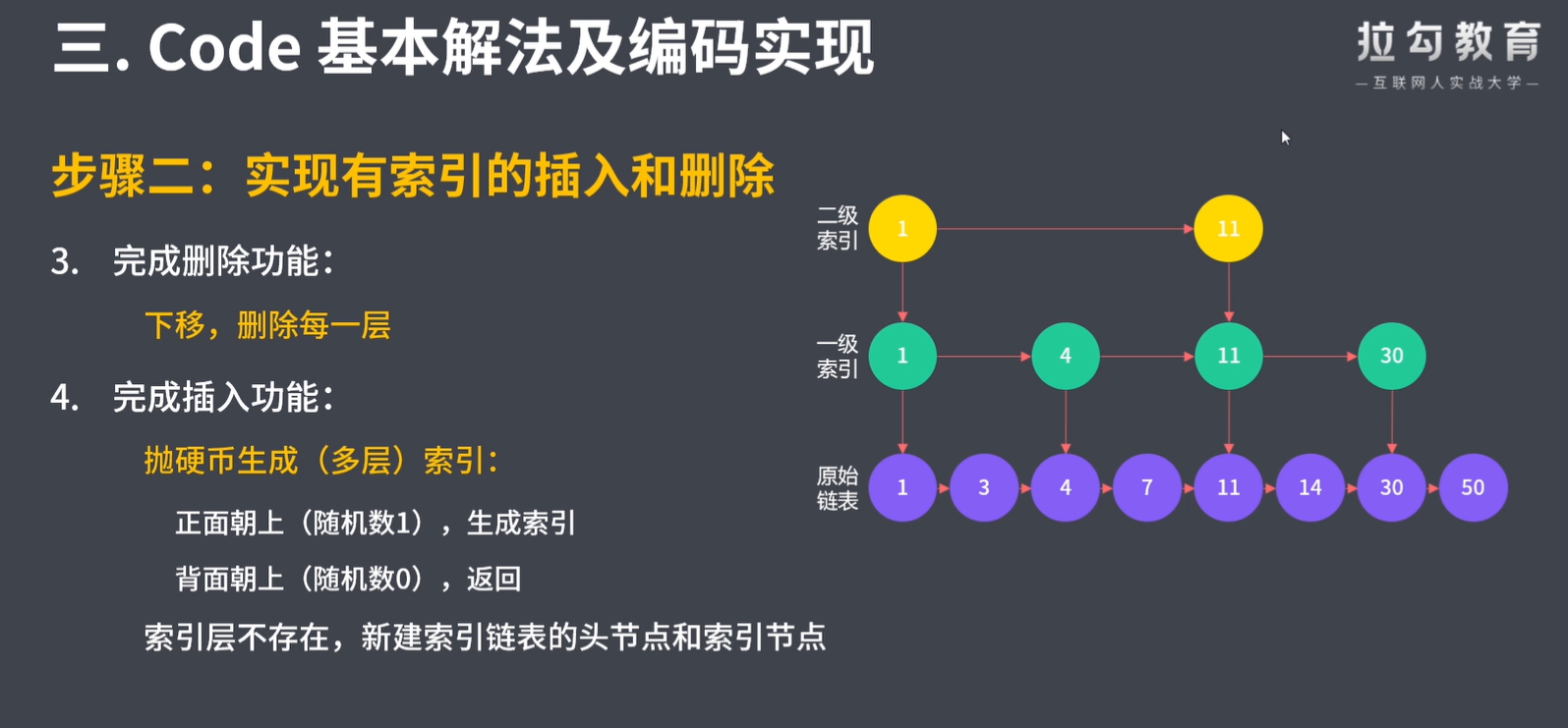
bool erase(int num): 在跳表中删除一个值,如果 num 不存在,直接返回false. 如果存在多个 num ,删除其中任意一个即可。
注意,跳表中可能存在多个相同的值,你的代码需要处理这种情况。
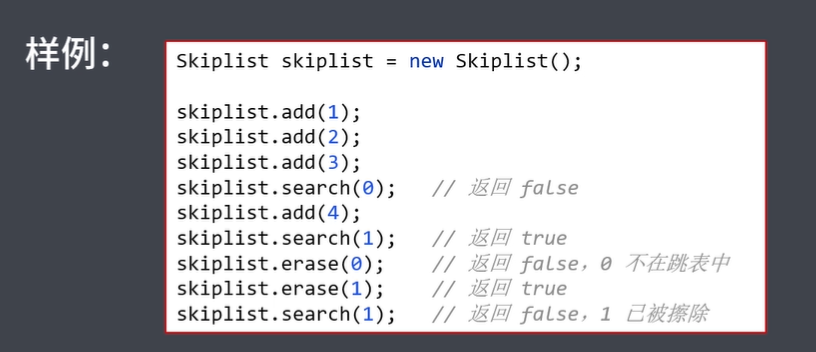
样例:
Skiplist skiplist = new Skiplist();
skiplist.add(1);
skiplist.add(2);
skiplist.add(3);
skiplist.search(0); // 返回 false
skiplist.add(4);
skiplist.search(1); // 返回 true
skiplist.erase(0); // 返回 false,0 不在跳表中
skiplist.erase(1); // 返回 true
skiplist.search(1); // 返回 false,1 已被擦除
约束条件:
0 <= num, target <= 20000
最多调用 50000 次 search, add, 以及 erase操作。
代码
class Skiplist { final int HEAD_VALUE = -1; // 链表头节点的值 final Node HEAD = new Node(HEAD_VALUE); Node head; // 最左上角的头节点,所有操作的开始位置 int levels; // 当前层级,即 head 节点所在的最高层数 int length; // 跳表长度,即原链表节点个数 public Skiplist() { head = HEAD; levels = 1; length = 1; // 仅包含头节点 } class Node { int val; Node right, down; Node(int val) { this(val, null, null); } Node(int val, Node right, Node down) { this.val = val; this.right = right; this.down = down; } } /** * 插入节点。将节点插入到原链表中正确的排序位置。 * * 1.定位插入位置:原链表中 >= num 的最小节点前 * 2.插入新节点 * 3.根据扔硬币决定(是否)生成索引 * * @param num */ public void add(int num) { // 1.定位插入位置:原链表中 > num 的最小节点前 Node node = head; // 从 head 开始查找 // 节点向下,可能是生成索引的位置,使用数组记录这些节点 Node[] nodes = new Node[levels]; int i = 0; // 操作上述数组 while (node != null) { // node==null 时,到达原链表 // 在同一层级上向右查找,直到链表结尾,或者找到 while (node.right != null && node.right.val < num) { node = node.right; } // 右侧为结尾 or 右侧值大 or 右侧值相同 nodes[i++] = node; // 继续查找下一层的位置 node = node.down; } // 2.插入新节点 node = nodes[--i]; // nodes中最后一个元素 Node newNode = new Node(num, node.right, null); node.right = newNode; length++; // 每添加一个节点,长度加 1 // 3.根据扔硬币决定(是否)生成索引 addIndicesByCoinFlip(newNode, nodes, i); // i 的值代表索引层数,不包含原链表 } /** * 抛硬币的方式决定是否给新节点建立索引。 * 索引层级可能超出现有跳表的层数,再抛一次决定是否生成索引。 * 1.抛硬币,在现有跳表层数范围内建立索引 * 2.抛硬币,决定是否建立一层超出跳表层数的索引层 * * @param target 新节点 * @param nodes 可能在这些节点后添加新索引节点 * @param indices 当前索引层数 */ private void addIndicesByCoinFlip(Node target, Node[] nodes, int indices) { Node downNode = target; Random random = new Random(); int coins = random.nextInt(2); // 0 or 1, 50% 概率 // 1.抛硬币,在现有跳表层数范围内建立索引 while (coins == 1 && levels < (length >> 6)) { if (indices > 0) { Node prev = nodes[--indices]; // 数组的倒数第二个元素,level 2 Node newIndex = new Node(target.val, prev.right, downNode); prev.right = newIndex; downNode = newIndex; coins = random.nextInt(2); } else { // 新建一个索引层级 // 新建索引节点和 head 节点 Node newIndex = new Node(target.val, null, downNode); Node newHead = new Node(HEAD_VALUE, newIndex, head); head = newHead; // head 指针上移 levels++; // 跳表层数加 1 } } } /** * 从 head 开始,从左到右、从上到下依次查找 * 1.小于,往右 * 2.相同,则返回 * 3.链表结尾,或大于,往下 * * @param target * @return */ public boolean search(int target) { Node n = get(target, head); return n != null; } /** * 遍历跳表,查找与给定值相同的节点,删除每一层 * 1.获取该指定数据节点的前一个节点 * 2.与当前层链表断开 * 3.下移,删除每一层 * * @param num * @return */ public boolean erase(int num) { boolean exist = false; Node node = get(num, head); while (node != null) { Node right = node.right; // 要删除的节点 node.right = right.right; right.right = null; // help GC exist = true; node = get(num, node.down); } if (exist) { length--; // 每删除一个节点,长度减 1 } return exist; } public Node get(int target, Node from) { Node n = from; while (n != null) { // 1.在同一层级上向右查找,直到链表结尾,或者找到 while (n.right != null && n.right.val < target) { n = n.right; } // 2.若找到,返回true Node right = n.right; // 要查找的节点 if (right != null && right.val == target) { return n; // 返回要查找的节点的前一个 } // 3.若右侧数据较大,向下一层 n = n.down; } return null; } } /** * Your Skiplist object will be instantiated and called as such: * Skiplist obj = new Skiplist(); * boolean param_1 = obj.search(target); * obj.add(num); * boolean param_3 = obj.erase(num); */



 浙公网安备 33010602011771号
浙公网安备 33010602011771号