ALG 3-5: Connectivity in Directed Graphs (有向图的连接性)
Directed Graphs
Directed graph. G = (V, E)
- Edge (u, v) goes from node u to node v.
Ex. Web graph -hyperlink points from one web page to another. (网络图——从一个网页到另一个网页的超链接)
- Directedness of graph is crucial. (图的方向性至关重要)
- Modern web search engines exploit hyperlink structure to rank web pages by importance. (搜索引擎利用超链接结构按重要性对网页进行排名)
Graph Search (社交图谱搜索)
Directed reachability. Given a node s, find all nodes reachable from s. (可达性:给定一个节点s,找出s可到达的所有节点。)
Directed s-t shortest path problem. Given two node s and t, what is the length of the shortest path between s and t?
(有向s-t最短路径问题: 给定两个节点s和t, s和t之间的最短路径的长度是多少?)
Graph search. BFS extends naturally to directed graphs. (图搜索: BFS这一方法可以自然地应用到有向图搜索)
Web crawler. Start from web page s. Find all web pages linked from s, either directly or indirectly.
(网络爬虫:从网页s开始,找到所有直接或间接从s链接的网页)
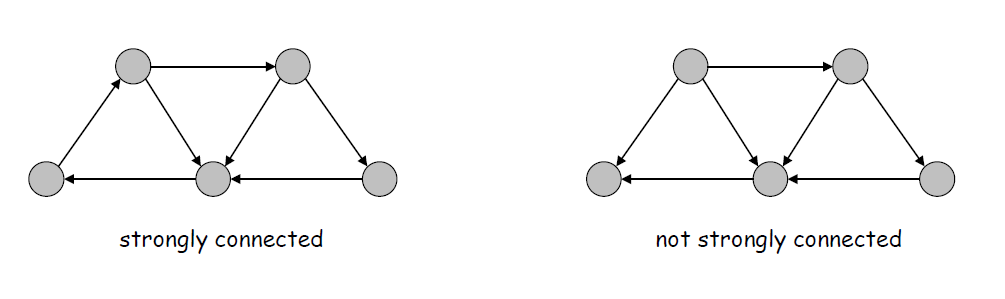
Strong Connectivity (强连通性)
Def. Node u and v are mutually reachable if there is a path from u to v and also a path from v to u.
(定义: 如果存在一条从u到v的路径和一条从v到u的路径,则节点u和v是相互可达的)
Def. A graph is strongly connected if every pair of nodes is mutually reachable.
(定义:一个图是强连通的,如果每个节点对都是相互可达的)
Lemma. Let s be any node. G is strongly connected iff every node is reachable from s, and s is reachable from every node.
(引理: 取任意节点。当且仅当 每个节点都可从s到达时,且s也是每个节点都可到达的 时,G是强连通的)
Pf. ⇐ Path from u to v: concatenate u-s path with s-v path. (从u到v的路径: 将u-s路径与s-v路径连接)
Path from v to u: concatenate v-s path with s-u path. (从v到u的路径:将v-s路径与s-u路径连接)

Strong Connectivity: Algorithm
Theorem. Can determine if G is strongly connected in O(m + n) time. (可以在O(m + n)时间内, 判断G是否强连通)
Proof.
- Pick any node s.
- Run BFS from s in G. // 从s节点出发, 正向运行BFS算法
- Run BFS from s in G_rev. (reverse orientation of every edge in G) // 从s节点出发, 反向运行BFS算法
- Return true iff all nodes reached in both BFS executions.
- Correctness follows immediately from previous lemma.