练习选讲(2023.7-8)
7 月
7.5
P2607 [ZJOI2008] 骑士:基环树,树上 dp(紫)
考虑断环成链,在每棵基环树上找到环上的两个点 \(r_1,r_2\),断开边 \((r_1,r_2)\),分别做一次树上 dp:令 \(f_{i,0/1}\) 表示对于第 \(i\) 个节点,选/不选的战斗力最大值,则状态转移方程为:
其中,\(j\) 为 \(i\) 的儿子节点。
则这棵基环树对答案的贡献为 \(\max(f_{r_1,0},f_{r_2,0})\)。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
typedef long long ll;
const int N = 1e6+10;
int n, r1, r2, w[N];
ll ans, f[N][2];
bool check[N], del[N<<1];
int idx = 1, h[N<<1], e[N<<1], ne[N<<1];
void add(int a, int b) {
e[++ idx] = b, ne[idx] = h[a], h[a] = idx;
}
bool find(int u, int edge) { // 找环上相邻两点
check[u] = 1;
for (int i = h[u]; i != -1; i = ne[i]) {
int v = e[i];
if ((i^1) == edge) continue;
if (!check[v]) {if (find(v, i)) return 1;}
else {del[i] = del[i^1] = 1, r1 = u, r2 = v; return 1;}
}
return 0;
}
ll dfs(int u, int edge) { // 树上 dp
check[u] = 1, f[u][0] = 0, f[u][1] = w[u];
for (int i = h[u]; i != -1; i = ne[i]) {
int v = e[i];
if ((i^1) == edge || del[i]) continue;
dfs(v, i);
f[u][0] += max(f[v][0], f[v][1]), f[u][1] += f[v][0];
}
return f[u][0];
}
int main() {
memset(h, -1, sizeof h);
scanf("%d", &n);
for (int i = 1, x; i <= n; ++i) {
scanf("%d%d", &w[i], &x);
add(i, x), add(x, i);
}
for (int i = 1; i <= n; ++i) {
if (check[i]) continue;
r1 = r2 = 0;
find(i, 0);
if (r1) {
ll ans1 = dfs(r1, 0), ans2 = dfs(r2, 0);
ans += max(ans1, ans2);
}
}
printf("%lld\n", ans);
return 0;
}
P1453 城市环路:基环树,树上 dp(蓝)
上面那道题的弱化版 qwq
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <iomanip>
#include <cstring>
using namespace std;
const int N = 1e5+10;
int n, r1, r2, p[N]; double k;
int ans, f[N][2];
bool check[N], del[N<<1];
int idx = 1, e[N<<1], h[N<<1], ne[N<<1];
void add(int a, int b) {
e[++ idx] = b, ne[idx] = h[a], h[a] = idx;
}
bool find(int u, int edge) {
check[u] = 1;
for (int i = h[u]; i != -1; i = ne[i]) {
int v = e[i];
if ((i^1) == edge) continue;
if (!check[v]) {if (find(v, i)) return 1;}
else {del[i] = del[i^1] = 1, r1 = u, r2 = v; return 1;}
}
return 0;
}
int dfs(int u, int edge) {
check[u] = 1, f[u][0] = 0, f[u][1] = p[u];
for (int i = h[u]; i != -1; i = ne[i]) {
int v = e[i];
if ((i^1) == edge || del[i]) continue;
dfs(v, i);
f[u][0] += max(f[v][0], f[v][1]), f[u][1] += f[v][0];
}
return f[u][0];
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
memset(h, -1, sizeof h);
cin >> n;
for (int i = 1; i <= n; ++i) cin >> p[i];
for (int i = 1; i <= n; ++i) {
int u, v; cin >> u >> v;
u ++, v ++;
add(u, v), add(v, u);
}
cin >> k;
for (int i = 1; i <= n; ++i) {
if (check[i]) continue;
r1 = r2 = 0;
find(i, 0);
if (r1) {
int ans1 = dfs(r1, 0), ans2 = dfs(r2, 0);
ans = max(ans1, ans2);
}
}
cout << fixed << setprecision(1) << ans * k << '\n';
return 0;
}
7.6
P5022 [NOIP2018 提高组] 旅行:基环树(紫)
\(m=n-1\) 时,该图为一棵树,贪心 dfs 即可。
\(m=n\) 时,该图为一棵基环树,可以发现必定有一条边是不会经过的,枚举这一条边,取字典序最小的答案(注意判断树是否联通)。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <vector>
using namespace std;
typedef pair<int, int> pii;
const int N = 5010;
int n, m, pos; bool cmp;
vector<int> ans; vector<pii> ed[N];
int idx = 1, s[N<<1], e[N<<1], h[N], ne[N<<1];
void add(int a, int b) {
e[++ idx] = b, ne[idx] = h[a], h[a] = idx, s[idx] = a;
ed[a].push_back({b, idx});
}
void dfs(int u, int fa) {
printf("%d ", u);
for (auto edg : ed[u]) {
int v = edg.first;
if (v != fa) dfs(v, u);
}
}
bool check(int u, int v, int fa, int num, int edge) { // 判断删掉 edge 边后是否为一棵树
if (v == u) return 1; if (num > n) return 0;
for (int i = h[v]; i != -1; i = ne[i]) {
int k = e[i];
if (i == edge || (i^1) == edge || k == fa) continue;
if (check(u, k, v, num+1, edge)) return 1;
}
return 0;
}
bool solve(int u, int fa, int edge) {
if (u > ans[pos] && !cmp) return 0;
if (u < ans[pos]) cmp = 1;
if (cmp) ans[pos] = u;
pos ++;
for (auto edg : ed[u]) {
int v = edg.first, t = edg.second;
if (v == fa || t == edge || (t^1) == edge) continue;
if (!solve(v, u, edge))
return 0;
}
return 1;
}
int main() {
memset(h, -1, sizeof h);
scanf("%d%d", &n, &m);
int u, v;
for (int i = 1; i <= m; ++i) {
scanf("%d%d", &u, &v);
add(u, v), add(v, u);
}
for (int i = 1; i <= n; ++i) sort(ed[i].begin(), ed[i].end());
if (m == n-1) dfs(1, 0);
else {
for (int i = 1; i <= n; ++i) ans.push_back(n);
for (int j = 1, i; j <= m; ++j) {
i = 2*j, pos = 0, cmp = 0;
if (!check(s[i], e[i], 0, 0, i)) continue;
solve(1, 1, i);
}
for (auto u : ans) printf("%d ", u);
}
return 0;
}
7.8
P1344 [USACO4.4] 追查坏牛奶 Pollutant Control:网络流(紫)
最小割模版题。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <queue>
using namespace std;
typedef long long ll;
const int N = 35, M = 2e3+10, INF = 2e9;
int n, m;
bool check[M];
int idx = 1, e[M], ne[M], h[N], c[M];
int pre[N], f[N];
void add(int u, int v, int w) {
e[++ idx] = v, ne[idx] = h[u], c[idx] = w, h[u] = idx;
}
bool bfs() {
memset(f, 0, sizeof f), memset(pre, 0, sizeof pre), f[1] = INF;
queue<int> q; q.push(1);
while (q.size()) {
int u = q.front(); q.pop();
for (int i = h[u]; i != -1; i = ne[i]) {
int v = e[i];
if (!f[v] && c[i]) {
f[v] = min(f[u], c[i]), pre[v] = i;
q.push(v);
if (v == n) return 1;
}
}
}
return 0;
}
ll EK() {
ll flow = 0;
while (bfs()) {
int v = n;
while (v != 1) {
int i = pre[v];
c[i] -= f[n], c[i^1] += f[n], v = e[i^1];
}
flow += (ll)f[n];
}
return flow;
}
int main() {
memset(h, -1, sizeof h);
scanf("%d%d", &n, &m);
for (int i = 1; i <= m; ++i) {
int u, v, w; scanf("%d%d%d", &u, &v, &w);
add(u, v, w), add(v, u, 0);
if (w) check[i*2] = 1;
}
ll max_flow = EK();
printf("%lld ", max_flow);
for (int i = 2; i <= m*2; i += 2) {
if (!c[i] && check[i]) c[i] = 1; else c[i] = INF;
c[i^1] = 0;
}
ll min_cut = EK();
printf("%lld ", min_cut);
return 0;
}
P2740 [USACO4.2] 草地排水Drainage Ditches:网络流(蓝)
最大流的双倍经验,用来练 Dinic。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <queue>
using namespace std;
typedef long long ll;
const int N = 210, M = 10010, INF = 2e9;
int n, m, S, T;
int idx = 1, e[M], ne[M], h[N]; ll c[M];
int d[N], cur[N]; // 当前弧
void add(int u, int v, int w) {
e[++ idx] = v, ne[idx] = h[u], c[idx] = w, h[u] = idx;
}
bool bfs() {
memset(d, 0, sizeof d);
queue<int> q; q.push(S), d[S] = 1, cur[S] = h[S];
while (!q.empty()) {
int u = q.front(); q.pop();
for (int i = h[u]; i != -1; i = ne[i]) {
int v = e[i];
if (!d[v] && c[i] > 0) {
d[v] = d[u] + 1, q.push(v), cur[v] = h[v];
if (v == T) return 1;
}
}
}
return 0;
}
ll dfs(int u, ll mf) {
if (u == T) return mf;
ll sum = 0;
for (int i = cur[u]; i != -1; i = ne[i]) {
cur[u] = i;
int v = e[i];
if (d[v] == d[u]+1 && c[i] > 0) {
ll f = dfs(v, min(mf, c[i]));
c[i] -= f, c[i^1] += f, sum += f, mf -= f;
if (!mf) break;
}
}
if (!sum) d[u] = 0;
return sum;
}
ll dinic() {
ll flow = 0;
while (bfs()) flow += dfs(S, INF);
return flow;
}
int main() {
memset(h, -1, sizeof h);
scanf("%d%d%d%d", &n, &m, &S, &T);
for (int i = 1; i <= m; ++i) {
int u, v, w; scanf("%d%d%d", &u, &v, &w);
add(u, v, w), add(v, u, 0);
}
ll flow = dinic();
printf("%lld\n", flow);
return 0;
}
P2065 [TJOI2011] 卡片:网络流,线性筛(蓝)
考虑朴素建图:建一个源点和汇点,从源点向 \(a_i\) 连一条容量为 \(1\) 的边,从 \(b_i\) 向汇点连一条容量为 \(1\) 的边,暴力判断是否存在大于 \(1\) 的公因数并连边。
发现这样做会超时。可以将 \(a_i\) 向自己的质因数连一条容量为 \(1\) 的边,\(b_i\) 的质因数向其连一条容量为 \(1\) 的边,再跑 dinic。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <queue>
#include <cstring>
using namespace std;
const int N = 5e5+10, M = 1e6+10, INF = 1e9;
int T, n, m, s, t;
int a[N], b[N];
int idx, e[M], ne[M], h[N], c[M];
int d[N], cur[N];
int prime[N], cnt; bool st[N];
void Euler() {
st[1] = 1;
for (int i = 2; i < N; ++i) {
if (!st[i]) prime[++ cnt] = i;
for (int j = 1; j <= cnt && prime[j] <= N/i; ++j) {
st[i*prime[j]] = 1;
if (i % prime[j] == 0) break;
}
}
}
void add(int u, int v, int w) {
e[++ idx] = v, ne[idx] = h[u], c[idx] = w, h[u] = idx;
}
bool bfs() {
memset(d, 0, sizeof d), d[s] = 1;
queue<int> q; q.push(s), cur[s] = h[s];
while (!q.empty()) {
int u = q.front(); q.pop();
for (int i = h[u]; i != -1; i = ne[i]) {
int v = e[i];
if (!d[v] && c[i] > 0) {
d[v] = d[u]+1, cur[v] = h[v], q.push(v);
if (v == t) return 1;
}
}
}
return 0;
}
int dfs(int u, int mf) {
if (u == t) return mf;
int sum = 0;
for (int i = cur[u]; i != -1; i = ne[i]) {
cur[u] = i;
int v = e[i];
if (d[v] == d[u]+1 && c[i] > 0) {
int f = dfs(v, min(mf, c[i]));
c[i] -= f, c[i^1] += f, sum += f, mf -= f;
if (!mf) break;
}
}
if (!sum) d[u] = 0;
return sum;
}
int dinic() {
int flow = 0;
while (bfs()) flow += dfs(s, INF);
return flow;
}
void solve() {
idx = 1, memset(h, -1, sizeof h);
scanf("%d%d", &n, &m); s = 0, t = n+m+1;
for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
for (int i = 1; i <= m; ++i) scanf("%d", &b[i]);
for (int i = 1; i <= n; ++i) {
add(0, i, 1), add(i, 0, 0);
for (int j = 1; j <= cnt && prime[j] <= a[i]; ++j)
if (a[i] % prime[j] == 0) add(i, n+m+j+1, 1), add(n+m+j+1, i, 0);
}
for (int i = 1; i <= m; ++i) {
add(n+i, n+m+1, 1), add(n+m+1, n+i, 0);
for (int j = 1; j <= cnt && prime[j] <= b[i]; ++j)
if (b[i] % prime[j] == 0) add(n+m+j+1, n+i, 1), add(n+i, n+m+j+1, 0);
}
int ans = dinic();
printf("%d\n", ans);
}
int main() {
Euler();
scanf("%d", &T);
while (T -- ) solve();
return 0;
}
P4001 [ICPC-Beijing 2006] 狼抓兔子:网络流(紫)
最小割板子题。注意反向边的容量和正向边容量都为 \(w\)。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <queue>
using namespace std;
const int N = 1e6+10, M = 6*N;
int n, m, s, t;
int idx = 1, e[M], ne[M], h[N], c[M];
int d[N], cur[N];
void add(int u, int v, int w) {
e[++ idx] = v, ne[idx] = h[u], c[idx] = w, h[u] = idx;
}
bool bfs() {
memset(d, 0, sizeof d), d[s] = 1;
queue<int> q; q.push(s), cur[s] = h[s];
while (!q.empty()) {
int u = q.front(); q.pop();
for (int i = h[u]; i != -1; i = ne[i]) {
int v = e[i];
if (!d[v] && c[i] > 0) {
d[v] = d[u]+1, cur[v] = h[v], q.push(v);
if (v == t) return 1;
}
}
}
return 0;
}
int dfs(int u, int mf) {
if (u == t) return mf;
int sum = 0;
for (int i = cur[u]; i != -1; i = ne[i]) {
cur[u] = i;
int v = e[i];
if (d[v] == d[u]+1 && c[i] > 0) {
int f = dfs(v, min(mf, c[i]));
c[i] -= f, c[i^1] += f, sum += f, mf -= f;
}
if (!mf) break;
}
if (!sum) d[u] = 0;
return sum;
}
int dinic() {
int flow = 0;
while (bfs()) flow += dfs(s, 1e9);
return flow;
}
int main() {
memset(h, -1, sizeof h);
scanf("%d%d", &n, &m); s = 1, t = n*m;
int u, v, w;
for (int i = 1; i <= n; ++i) {
for (int j = 1; j < m; ++j)
scanf("%d", &w), u = (i-1)*m+j, v = (i-1)*m+j+1, add(u, v, w), add(v, u, w);
}
for (int i = 1; i < n; ++i) {
for (int j = 1; j <= m; ++j)
scanf("%d", &w), u = (i-1)*m+j, v = i*m+j, add(u, v, w), add(v, u, w);
}
for (int i = 1; i < n; ++i) {
for (int j = 1; j < m; ++j) {
scanf("%d", &w), u = (i-1)*m+j, v = i*m+j+1, add(u, v, w), add(v, u, w);
}
}
int ans = dinic();
printf("%d\n", ans);
return 0;
}
P2763 试题库问题:网络流(蓝)
建一个源点,\(k\) 个表示题目类型的点,\(n\) 个表示题目的点和一个汇点。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <queue>
using namespace std;
const int N = 5e3+10, M = 1e5+10;
int k, n, m, s, t;
int idx = 1, e[M], ne[M], h[N], c[M];
int d[N], cur[N];
void add(int u, int v, int w) {
e[++ idx] = v, ne[idx] = h[u], c[idx] = w, h[u] = idx;
}
bool bfs() {
memset(d, 0, sizeof d), d[s] = 1;
queue<int> q; q.push(s), cur[s] = h[s];
while (!q.empty()) {
int u = q.front(); q.pop();
for (int i = h[u]; i != -1; i = ne[i]) {
int v = e[i];
if (!d[v] && c[i] > 0) {
d[v] = d[u]+1, cur[v] = h[v], q.push(v);
if (v == t) return 1;
}
}
}
return 0;
}
int dfs(int u, int mf) {
if (u == t) return mf;
int sum = 0;
for (int i = h[u]; i != -1; i = ne[i]) {
cur[u] = i;
int v = e[i];
if (d[v] == d[u]+1 && c[i] > 0) {
int f = dfs(v, min(mf, c[i]));
c[i] -= f, c[i^1] += f, sum += f, mf -= f;
}
if (!mf) break;
}
if (!sum) d[u] = 0;
return sum;
}
int dinic() {
int flow = 0;
while (bfs()) flow += dfs(s, 1e9);
return flow;
}
int main() {
memset(h, -1, sizeof h);
scanf("%d%d", &k, &n), s = 0, t = n+k+1;
int u, v, w;
for (int i = 1; i <= k; ++i) scanf("%d", &w), u = s, v = i, add(u, v, w), add(v, u, 0), m += w;
for (int i = 1; i <= n; ++i) {
int p; scanf("%d", &p);
while (p -- ) scanf("%d", &u), v = k+i, add(u, v, 1), add(v, u, 0);
add(v, t, 1), add(t, v, 0);
}
int ans = dinic();
if (ans != m) puts("No Solution!"), exit(0);
for (int u = 1; u <= k; ++u) {
printf("%d: ", u);
for (int i = h[u]; i != -1; i = ne[i]) {
int v = e[i];
if (!c[i] && v) printf("%d ", v-k);
}
puts("");
}
return 0;
}
惠州集训(7.10-7.19)
7.10(Day 1)
P2590 [ZJOI2008] 树的统计:树链剖分,线段树(蓝)
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <vector>
#include <cstring>
using namespace std;
#define int long long
const int N = 3e4+10, INF = 3e6;
int n, m, a[N];
vector<int> e[N];
int idx, id[N], w[N];
int dep[N], f[N], son[N], size[N], top[N];
void get_son(int u, int fa) {
dep[u] = dep[fa] + 1, f[u] = fa, size[u] = 1;
for (auto v : e[u]) {
if (v == fa) continue;
get_son(v, u), size[u] += size[v];
if (size[v] > size[son[u]]) son[u] = v;
}
}
void get_top(int u, int t) {
if (!u) return ;
top[u] = t, id[u] = ++ idx, w[idx] = a[u];
get_top(son[u], t);
for (auto v : e[u]) {
if (v == f[u] || v == son[u]) continue;
get_top(v, v);
}
}
struct Node {
int l, r, maxl, sum;
} seg[N<<2];
void pushup(int u) {
seg[u].sum = seg[u<<1].sum + seg[u<<1|1].sum;
seg[u].maxl = max(seg[u<<1].maxl, seg[u<<1|1].maxl);
}
void build(int u, int l, int r) {
seg[u].l = l, seg[u].r = r;
if (l == r) seg[u].maxl = seg[u].sum = w[l];
else {
int mid = l + r >> 1;
build(u<<1, l, mid), build(u<<1|1, mid+1, r);
pushup(u);
}
}
int query_maxl(int u, int l, int r) {
if (seg[u].l >= l && seg[u].r <= r) return seg[u].maxl;
int mid = seg[u].l + seg[u].r >> 1, maxl = -INF;
if (l <= mid) maxl = max(maxl, query_maxl(u<<1, l, r));
if (r > mid) maxl = max(maxl, query_maxl(u<<1|1, l, r));
return maxl;
}
int query_sum(int u, int l, int r) {
if (seg[u].l >= l && seg[u].r <= r) return seg[u].sum;
int mid = seg[u].l + seg[u].r >> 1, sum = 0;
if (l <= mid) sum += query_sum(u<<1, l, r);
if (r > mid) sum += query_sum(u<<1|1, l, r);
return sum;
}
void modify(int u, int pos, int v) {
if (seg[u].l == pos && seg[u].r == pos) seg[u].sum = seg[u].maxl = v;
else {
int mid = seg[u].l + seg[u].r >> 1;
if (pos <= mid) modify(u<<1, pos, v);
else modify(u<<1|1, pos, v);
pushup(u);
}
}
int ask_maxl(int u, int v) {
int maxl = -INF;
while (top[u] != top[v]) {
if (dep[top[u]] < dep[top[v]]) swap(u, v);
maxl = max(maxl, query_maxl(1, id[top[u]], id[u]));
u = f[top[u]];
}
if (dep[u] > dep[v]) swap(u, v);
maxl = max(maxl, query_maxl(1, id[u], id[v]));
return maxl;
}
int ask_sum(int u, int v) {
int sum = 0;
while (top[u] != top[v]) {
if (dep[top[u]] < dep[top[v]]) swap(u, v);
sum += query_sum(1, id[top[u]], id[u]);
u = f[top[u]];
}
if (dep[u] > dep[v]) swap(u, v);
sum += query_sum(1, id[u], id[v]);
return sum;
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n;
for (int i = 1; i < n; ++i) {
int u, v; cin >> u >> v;
e[u].push_back(v), e[v].push_back(u);
}
for (int i = 1; i <= n; ++i) cin >> a[i];
get_son(1, 1), get_top(1, 1);
build(1, 1, n);
cin >> m;
string op; int u, v;
while (m -- ) {
cin >> op >> u >> v;
if (op == "CHANGE") modify(1, id[u], v);
else if (op == "QMAX") cout << ask_maxl(u, v) << '\n';
else cout << ask_sum(u, v) << '\n';
}
return 0;
}
P3178 [HAOI2015] 树上操作:树链剖分,线段树(蓝)
由于是 dfs 计算 id,子树内的编号也必然连续。做完了。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <vector>
using namespace std;
#define int long long
const int N = 1e5+10;
int n, m, a[N];
int dep[N], f[N], son[N], size[N], top[N];
int idx, w[N], id[N];
vector<int> e[N];
void get_son(int u, int fa) {
dep[u] = dep[fa]+1, f[u] = fa, size[u] = 1;
for (auto v : e[u]) {
if (v == fa) continue;
get_son(v, u), size[u] += size[v];
if (size[v] > size[son[u]]) son[u] = v;
}
}
void get_top(int u, int t) {
if (!u) return ;
id[u] = ++ idx, w[idx] = a[u], top[u] = t;
get_top(son[u], t);
for (auto v : e[u]) {
if (v == f[u] || v == son[u]) continue;
get_top(v, v);
}
}
struct Node {
int l, r, sum, add;
} seg[N<<2];
void pushup(int u) {
seg[u].sum = seg[u<<1].sum + seg[u<<1|1].sum;
}
void pushdown(int u) {
if (!seg[u].add) return ;
seg[u<<1].sum += seg[u].add * (seg[u<<1].r-seg[u<<1].l+1);
seg[u<<1|1].sum += seg[u].add * (seg[u<<1|1].r-seg[u<<1|1].l+1);
seg[u<<1].add += seg[u].add, seg[u<<1|1].add += seg[u].add;
seg[u].add = 0;
}
void build(int u, int l, int r) {
seg[u].l = l, seg[u].r = r, seg[u].add = 0;
if (l == r) seg[u].sum = w[l];
else {
int mid = l + r >> 1;
build(u<<1, l, mid), build(u<<1|1, mid+1, r);
pushup(u);
}
}
int query(int u, int l, int r) {
if (seg[u].l >= l && seg[u].r <= r) return seg[u].sum;
pushdown(u);
int mid = seg[u].l + seg[u].r >> 1, sum = 0;
if (l <= mid) sum += query(u<<1, l, r);
if (r > mid) sum += query(u<<1|1, l, r);
return sum;
}
void modify(int u, int l, int r, int v) {
if (seg[u].l >= l && seg[u].r <= r) seg[u].sum += (seg[u].r-seg[u].l+1)*v, seg[u].add += v;
else {
pushdown(u);
int mid = seg[u].l + seg[u].r >> 1;
if (l <= mid) modify(u<<1, l, r, v);
if (r > mid) modify(u<<1|1, l, r, v);
pushup(u);
}
}
int ask_path(int u) {
int sum = 0;
while (top[u] != 1) {
sum += query(1, id[top[u]], id[u]);
u = f[top[u]];
}
sum += query(1, id[1], id[u]);
return sum;
}
signed main() {
scanf("%lld%lld", &n, &m);
for (int i = 1; i <= n; ++i) scanf("%lld", &a[i]);
for (int i = 1; i < n; ++i) {
int u, v; scanf("%lld%lld", &u, &v);
e[u].push_back(v), e[v].push_back(u);
}
get_son(1, 1), get_top(1, 1);
build(1, 1, n);
int op, x, a;
while (m -- ) {
scanf("%lld%lld", &op, &x);
if (op == 1) scanf("%lld", &a), modify(1, id[x], id[x], a);
else if (op == 2) scanf("%lld", &a), modify(1, id[x], id[x]+size[x]-1, a);
else printf("%lld\n", ask_path(x));
}
return 0;
}
P2087 GTY的人类基因组计划2:异或 hash,思维(紫)
随机每个人的权值,用一个 unordered_map 记录每个房间的权值(房间的权值为其中所有人的权值异或和)。用一个 set 存储哪些房间对答案有贡献,注意实现细节,以及随机种子的选取。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <set>
#include <unordered_map>
#include <chrono>
#include <random>
using namespace std;
const int N = 1e5+10;
typedef set<int>::iterator it;
int n, m, q, a[N], p[N], now[N], num[N];
set<int> s;
unordered_map<int, bool> nums;
int main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m >> q;
mt19937 gen(chrono::system_clock::now().time_since_epoch().count());
for (int i = 1; i <= n; ++i) a[i] = gen() % 1000000000, num[1] ^= a[i], now[i] = 1;
s.insert(1), p[1] = n;
char op; int x, y;
while (q -- ) {
cin >> op >> x >> y;
if (op == 'C') {
if (now[x] == y) continue;
s.erase(now[x]), s.erase(y);
p[now[x]] --, p[y] ++;
num[now[x]] ^= a[x], num[y] ^= a[x];
if (!nums[num[now[x]]]) s.insert(now[x]);
if (!nums[num[y]]) s.insert(y);
now[x] = y;
} else {
int sum = 0;
it pos = s.lower_bound(x);
for ( ; pos != s.end() && *pos <= y; ) {
sum += p[*pos];
nums[num[*pos]] = 1;
pos ++; it tmp = pos; tmp --;
s.erase(tmp);
}
cout << sum << '\n';
}
}
return 0;
}
P2216 [HAOI2007] 理想的正方形:二维 st 表(蓝)
二维 st 表板子。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
using namespace std;
const int N = 1010;
int a, b, n, ans = 1e9, c[N][N];
int st_max[N][N][8], st_min[N][N][8];
int query_max(int i, int j, int k) {
int t = log2(k);
return max(max(st_max[i][j][t], st_max[i+k-(1<<t)][j+k-(1<<t)][t]),
max(st_max[i+k-(1<<t)][j][t], st_max[i][j+k-(1<<t)][t]));
}
int query_min(int i, int j, int k) {
int t = log2(k);
return min(min(st_min[i][j][t], st_min[i+k-(1<<t)][j+k-(1<<t)][t]),
min(st_min[i+k-(1<<t)][j][t], st_min[i][j+k-(1<<t)][t]));
}
int main() {
scanf("%d%d%d", &a, &b, &n);
for (int i = 1; i <= a; ++i) {
for (int j = 1; j <= b; ++j)
scanf("%d", &c[i][j]);
}
for (int i = 1; i <= a; ++i) {
for (int j = 1; j <= b; ++j)
st_max[i][j][0] = st_min[i][j][0] = c[i][j];
}
for (int k = 1; k <= ceil(log2(n)); ++k) {
for (int i = 1; i <= a-(1<<k)+1; ++i) {
for (int j = 1; j <= b-(1<<k)+1; ++j)
st_max[i][j][k] = max(max(st_max[i][j][k-1], st_max[i+(1<<k-1)][j+(1<<k-1)][k-1]),
max(st_max[i][j+(1<<k-1)][k-1], st_max[i+(1<<k-1)][j][k-1])),
st_min[i][j][k] = min(min(st_min[i][j][k-1], st_min[i+(1<<k-1)][j+(1<<k-1)][k-1]),
min(st_min[i][j+(1<<k-1)][k-1], st_min[i+(1<<k-1)][j][k-1]));
}
}
for (int i = 1; i <= a-n+1; ++i) {
for (int j = 1; j <= b-n+1; ++j)
ans = min(ans, query_max(i, j, n)-query_min(i, j, n));
}
printf("%d\n", ans);
return 0;
}
P2294 [HNOI2005] 狡猾的商人:(*)并查集(蓝)
利用前缀和的思想,边带权并查集。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
#define int long long
const int N = 1010;
int q, n, m, p[N], dis[N]; // dis[i]表示i到父亲的距离
int find(int x) {
if (x == p[x]) return p[x];
int fa = find(p[x]); dis[x] += dis[p[x]], p[x] = fa; // 注意细节
return p[x];
}
signed main() {
scanf("%lld", &q);
while (q -- ) {
scanf("%lld%lld", &n, &m);
for (int i = 0; i <= n; ++i) p[i] = i, dis[i] = 0; // 预处理
int u, v, w; bool check = 1;
while (m -- ) {
scanf("%lld%lld%lld", &u, &v, &w);
u --;
int fu = find(u), fv = find(v);
if (fu != fv) p[fu] = fv, dis[fu] = w - dis[u] + dis[v]; // 前缀和,在纸上画一下
else if (dis[v] != dis[u]-w) check = 0; // 如果当前推出的前缀和与之前的不符
}
(check) ? puts("true") : puts("false");
}
return 0;
}
Day1 练习赛:
CF1194D. 1-2-K Game:NIM 博弈,数学(绿)
分三类讨论:
- \(k=3\) 时,根据取石子游戏的经典结论,可知 \(n\) 为 \(4\) 的倍数时先手必败;
- \(k\bmod 3\ne 0\) 时,\(k\) 对答案实际没有影响。这是因为 \(k\) 个石子时一定先手必胜。
- \(k\bmod 3=0\) 且 \(k\ne 3\):打表可得循环节为 \(k+1\),则 \(n\bmod 3=0\) 且 \(n\ne k\) 或 \(n=k+1\) 时先手必败。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
int t, n, k, f[110];
int main() {
scanf("%d", &t);
while (t -- ) {
scanf("%d%d", &n, &k);
if (k % 3 != 0) ((n % 3 == 0) ? puts("Bob") : puts("Alice"));
else if (k == 3) ((n % 4 == 0) ? puts("Bob") : puts("Alice"));
else {
n %= (k+1);
if ((n != k && n % 3 == 0) || (n == k+1)) puts("Bob");
else puts("Alice");
}
}
return 0;
}
P2389 电脑班的裁员:动态规划(蓝)
令 \(f_{i,j}\) 表示考虑前 \(i\) 个数,当前为第 \(j\) 段的最大值,则状态转移方程:
(其中 \(s_i\) 表示数组 \(a\) 的前缀和)
这样计算的时间复杂度是 \(O(n^3)\) 的,考虑优化。
计算 \(f_{i,j}\) 时,我们需要用到的状态为 \(s_i-s_0+f_{0,j-1},s_i-s_1+f_{1,j-1},\cdots,s_i-s_{i-2}+f_{i-2,j}\)。计算 \(f_{i+1,j}\) 时,我们需要用到的状态为 \(s_{i+1}-s_0+f_{0,j-1},s_{i+1}-s_1+f_{1,j-1},\cdots,s_{i+1}-s_{i-2}+f_{i-2,j}\)。注意到其中 \(f_{k,j-1}-s_0\) 的部分是相同的,可以令 \(premax\) 存储这个值,减少一重枚举 \(k\) 的循环。
时间复杂度 \(O(n^2)\)。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 2010;
int n, k, ans;
int a[N], s[N], f[N][N];
int main() {
scanf("%d%d", &n, &k);
for (int i = 1; i <= n; ++i) scanf("%d", &a[i]), s[i] = s[i-1] + a[i];
for (int j = 1; j <= k; ++j) {
int premax = f[0][j-1] - s[0];
for (int i = 1; i <= n; ++i) {
f[i][j] = max(f[i-1][j], premax+s[i]);
ans = max(ans, f[i][j]);
premax = max(premax, f[i][j-1]-s[i]);
}
}
printf("%d\n", ans);
return 0;
}
P2349 金字塔:最短路(绿)
枚举最长边 \(i\),强制钦定必须走 \(i\),dijkstra 求最短路。
时间复杂度 \(O(mn\log n)\)。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <queue>
using namespace std;
const int N = 210, M = 4010;
typedef pair<int, int> pii;
int n, m, ans = (int)2e9;
int idx = 1, e[M], ne[M], h[N], w[M];
int dist[N]; bool st[N];
void add(int a, int b, int c) {
e[++ idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx;
}
int dijkstra(int s, int t, int c) {
memset(dist, 0x3f, sizeof dist), memset(st, 0, sizeof st);
priority_queue<pii, vector<pii>, greater<pii>> q;
q.push({0, s}); dist[s] = 0;
while (!q.empty()) {
pii p = q.top(); q.pop();
int u = p.second, dis = p.first;
if (st[u]) continue;
if (u == t) break;
st[u] = 1;
for (int i = h[u]; i != -1; i = ne[i]) {
int v = e[i];
if (dist[v] > dis+w[i] && w[i] < c) {
dist[v] = dis+w[i];
if (!st[v]) q.push({dist[v], v});
}
}
}
return (dist[t] == 0x3f3f3f3f) ? 1e9 : dist[t];
}
int main() {
memset(h, -1, sizeof h);
scanf("%d%d", &n, &m);
for (int i = 1; i <= m; ++i) {
int u, v, w; scanf("%d%d%d", &u, &v, &w);
add(u, v, w), add(v, u, w);
}
for (int i = 2; i <= 2*m+1; ++i) {
int u = e[i^1], v = e[i], dist1 = dijkstra(1, u, w[i]), dist2 = dijkstra(v, n, w[i]);
ans = min(ans, dist1+w[i]*2+dist2);
}
printf("%d\n", ans);
return 0;
}
CF1368D. AND, OR and square sum:贪心,位运算(绿)
由于 \((x\text{\&}y)+(x\text{|}y)=x+y\),所以无论如何操作,\(\sum a_i\) 不变, 且所有 \(a_i\) 的二进制表示中 \(1\) 的数量不变。
还需要一个引理:若 \(x\ge 0\),则 \(x^2+(a-x)^2\) 在 \(x=a\) 或 \(0\) 时取得最大值 \(a^2\)。即,和一定,差越大,平方和越大。
那么贪心计算出所有数的平方和即可。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
#define int long long
typedef pair<int, int> pii;
const int N = 2e5+10;
int n, ans, a[N];
pii num[25];
void trans(int x) {
for (int i = 24; i >= 0 && x; --i) {
if (x >= (1<<i))
x -= (1<<i), num[i].first ++;
}
}
signed main() {
scanf("%lld", &n);
for (int i = 0; i <= 24; ++i) num[i].second = i;
for (int i = 1; i <= n; ++i) {
scanf("%lld", &a[i]);
trans(a[i]);
}
sort(num, num+25);
int s = (1 << 25) - 1;
for (int i = 0; i <= 24; ++i) {
ans += num[i].first * (s * s), s -= (1 << num[i].second);
for (int j = i+1; j <= 24; ++j) num[j].first -= num[i].first;
}
printf("%lld\n", ans);
return 0;
}
7.11(Day 2)
P3620 [APIO/CTSC2007] 数据备份:(*)反悔贪心,双向链表,堆(蓝)
由于要求电缆距离之和最短,所以一定选择相邻的两栋楼。令 \(d_i\) 表示第 \(i\) 座大楼和第 \(i+1\) 座大楼之间的距离,考虑贪心:选出当前最小的 \(d_i\),将 \(d_{i-1},d_i,d_{i+1}\) 删除。但这样可能会导致无法求得全局最小值。我们需要能够反悔的贪心。
考虑在取出 \(d_i\) 后如何才能取出 \(d_{i-1}\) 和 \(d_{i+1}\):令 \(d_i'=d_{i-1}+d_{i+1}-d_i\)。双向链表维护。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <queue>
using namespace std;
#define int long long
typedef pair<int, int> pii;
const int N = 1e5+10;
int n, k, ans, a[N]; bool check[N];
priority_queue<pii, vector<pii>, greater<pii>> q;
int L[N], R[N], val[N];
void del(int u) {
L[u] = L[L[u]], R[u] = R[R[u]];
R[L[u]] = u, L[R[u]] = u;
}
signed main() {
scanf("%lld%lld", &n, &k);
for (int i = 1; i <= n; ++i) {
scanf("%lld", &a[i]);
if (i == 1) continue;
int d = a[i]-a[i-1];
q.push({d, i}), L[i] = i-1, R[i] = i+1, val[i] = d;
}
val[1] = val[n+1] = (int)1e9;
while (k -- ) {
while (check[q.top().second]) q.pop();
auto t = q.top();
int u = t.second, v = t.first; q.pop();
check[L[u]] = check[R[u]] = 1;
ans += v;
val[u] = val[L[u]] + val[R[u]] - val[u];
q.push({val[u], u});
del(u);
}
printf("%lld\n", ans);
return 0;
}
P1484 种树:反悔贪心(蓝)
同上。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <queue>
using namespace std;
#define int long long
typedef pair<int, int> pii;
const int N = 5e5+10;
int n, k, ans, a[N];
int L[N], R[N]; bool check[N];
priority_queue<pii, vector<pii>> q;
void del(int u) {
L[u] = L[L[u]], R[u] = R[R[u]];
R[L[u]] = u, L[R[u]] = u;
}
signed main() {
scanf("%lld%lld", &n, &k);
for (int i = 1; i <= n; ++i) {
scanf("%lld", &a[i]);
L[i] = i-1, R[i] = i+1;
q.push({a[i], i});
}
while (k -- ) {
while (check[q.top().second]) q.pop();
auto t = q.top(); q.pop();
int u = t.second, v = t.first;
if (v < 0) break;
check[L[u]] = check[R[u]] = 1;
ans += v;
a[u] = a[L[u]] + a[R[u]] - a[u];
q.push({a[u], u});
del(u);
}
printf("%lld\n", ans);
return 0;
}
P1392 取数:堆(蓝)
借鉴 P1631 序列合并 的方法。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <queue>
#include <cstring>
using namespace std;
typedef pair<int, int> pii;
const int N = 810;
int n, m, k, a[N][N], idx, b[N], pos[N];
int main() {
scanf("%d%d%d", &n, &m, &k);
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= m; ++j)
scanf("%d", &a[i][j]);
}
sort(a[1]+1, a[1]+m+1);
for (int i = 2; i <= n; ++i) {
sort(a[i]+1, a[i]+m+1); idx = 0;
priority_queue<pii, vector<pii>, greater<pii>> q;
for (int j = 1; j <= k; ++j) q.push({a[i-1][j]+a[i][1], j}), pos[j] = 1;
for (int j = 1; j <= k; ++j) {
auto t = q.top(); q.pop();
int v = t.first, p = t.second;
b[++ idx] = v, pos[p] ++;
if (p*pos[p] <= k) q.push({a[i-1][p]+a[i][pos[p]], p}); // 关键优化,若p*pos[p]>k,则它前面一定有至少k个比它小的数,一定不会成为答案
}
for (int j = 1; j <= k; ++j) a[i][j] = b[j];
}
for (int i = 1; i <= k; ++i) printf("%d ", b[i]);
return 0;
}
P7453 [THUSCH2017] 大魔法师:线段树,矩阵乘法(紫)
线段树的节点维护矩阵 \([A\;B\;C\;1]\),通过转移矩阵进行区间操作。注意空间和时间优化。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
typedef long long ll;
const int N = 2.5e5+10, P = 998244353;
int n, m;
struct Matrix {
int a[5][5];
Matrix() {
memset(a, 0, sizeof a);
}
} base, op[8], ball[N];
void set_base(Matrix &a) {
for (int i = 1; i < 5; ++i) a.a[i][i] = 1;
}
Matrix operator*(const Matrix &x, const Matrix &y) {
Matrix ans;
for (int k = 1; k < 5; ++k) {
for (int i = 1; i < 5; ++i)
for (int j = 1; j < 5; ++j)
ans.a[i][j] = (ans.a[i][j] + (ll)x.a[i][k]*y.a[k][j]) % P;
}
return ans;
}
Matrix operator+(const Matrix &x, const Matrix &y) {
Matrix ans;
for (int i = 1; i < 5; ++i) {
for (int j = 1; j < 5; ++j)
ans.a[i][j] = ((ll)x.a[i][j] + y.a[i][j]) % P;
}
return ans;
}
void init() {
set_base(base);
for (int i = 1; i <= 6; ++i) set_base(op[i]);
op[1].a[2][1] = 1, op[2].a[3][2] = 1, op[3].a[1][3] = 1, op[6].a[3][3] = 0;
}
struct Node {
int l, r; Matrix t, tag;
} seg[N<<2];
void pushup(int u) {
seg[u].t = seg[u<<1].t + seg[u<<1|1].t;
}
void pushdown(int u) {
seg[u<<1].t = seg[u<<1].t * seg[u].tag, seg[u<<1|1].t = seg[u<<1|1].t * seg[u].tag;
seg[u<<1].tag = seg[u<<1].tag * seg[u].tag, seg[u<<1|1].tag = seg[u<<1|1].tag * seg[u].tag;
seg[u].tag = base;
}
void build(int u, int l, int r) {
seg[u].l = l, seg[u].r = r, seg[u].tag = base;
if (l == r) {
seg[u].t = ball[l];
return ;
}
int mid = l + r >> 1;
build(u<<1, l, mid), build(u<<1|1, mid+1, r);
pushup(u);
}
Matrix query(int u, int l, int r) {
if (seg[u].l >= l && seg[u].r <= r) return seg[u].t;
pushdown(u);
int mid = seg[u].l + seg[u].r >> 1; Matrix ans;
if (l <= mid) ans = ans + query(u<<1, l, r);
if (r > mid) ans = ans + query(u<<1|1, l, r);
return ans;
}
void modify(int u, int l, int r, int p) {
if (seg[u].l >= l && seg[u].r <= r) {
seg[u].t = seg[u].t * op[p], seg[u].tag = seg[u].tag * op[p];
return ;
}
pushdown(u);
int mid = seg[u].l + seg[u].r >> 1;
if (l <= mid) modify(u<<1, l, r, p);
if (r > mid) modify(u<<1|1, l, r, p);
pushup(u);
}
int main() {
init();
scanf("%d", &n);
int a, b, c;
for (int i = 1; i <= n; ++i) {
scanf("%d%d%d", &a, &b, &c);
ball[i].a[1][1] = a, ball[i].a[1][2] = b, ball[i].a[1][3] = c, ball[i].a[1][4] = 1;
}
build(1, 1, n);
scanf("%d", &m);
int p, l, r, v;
while (m -- ) {
scanf("%d%d%d", &p, &l, &r);
if (p == 1) modify(1, l, r, 1);
else if (p == 2) modify(1, l, r, 2);
else if (p == 3) modify(1, l, r, 3);
else if (p == 4) scanf("%d", &v), op[4].a[4][1] = v, modify(1, l, r, 4);
else if (p == 5) scanf("%d", &v), op[5].a[2][2] = v, modify(1, l, r, 5);
else if (p == 6) scanf("%d", &v), op[6].a[4][3] = v, modify(1, l, r, 6);
else {
Matrix ans = query(1, l, r);
printf("%d %d %d\n", ans.a[1][1], ans.a[1][2], ans.a[1][3]);
}
}
return 0;
}
P1901 发射站:单调栈(黄)
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <stack>
using namespace std;
const int N = 1e6+10;
stack<int> q;
int n, ans, h[N], v[N], s[N];
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) {
scanf("%d%d", &h[i], &v[i]);
while (q.size() && h[q.top()] < h[i]) s[i] += v[q.top()], q.pop();
if (q.size()) s[q.top()] += v[i]; q.push(i);
}
for (int i = 1; i <= n; ++i) ans = max(ans, s[i]);
printf("%d\n", ans);
return 0;
}
Day 2 模拟赛:
P1823 [COI2007] Patrik 音乐会的等待:(*)单调栈(蓝)
单调栈维护单调不升的 \(h_i\),每次弹出的数量(包括与 \(h_i\) 相等的数)即为 \(h_i\) 对答案的贡献。注意到直接弹出会 TLE,需要用一个 pair 来存储单调栈中的下标和出现的次数。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <stack>
using namespace std;
#define int long long
typedef pair<int, int> pii;
const int N = 5e5+10;
stack<pii> q;
int n, ans, h[N];
signed main() {
scanf("%lld", &n);
for (int i = 1; i <= n; ++i) {
scanf("%lld", &h[i]);
int cnt = 1;
while (q.size() && h[i] >= h[q.top().first]) {
if (h[q.top().first] == h[i]) cnt += q.top().second;
ans += q.top().second, q.pop();
}
if (q.size()) ans ++;
q.push({i, cnt});
}
printf("%lld\n", ans);
return 0;
}
P1836 数页码:打表 数学(?)(绿)
打表:每 \(10^7\) 个数记录一次前缀和。
\(0\sim 10^k-1\) 中,\(0\sim 9\) 总共出现了 \(k\cdot 10^k\) 次,所以每个数字出现了 \(k\cdot 10^{k-1}\) 次,数字和为 \(45k\cdot 10^{k-1}\)。由此可得,\(0\sim a\times 10^k-1\) 中,数字和为 \(45ak\cdot 10^{k-1}+\dfrac{a(a-1)}{2} \cdot 10^{k}\)。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
using namespace std;
typedef long long ll;
int n; ll ans;
int main() {
scanf("%d", &n);
for (int i = log10(n); i >= 0; --i) {
int t = n / (int)pow(10, i);
ans += (ll)45 * t * i * pow(10, i) / 10 + (ll)t * (t-1) / 2 * pow(10, i); // 处理t*10^i
ans += (ll)t * (n-t*pow(10, i)+1); // 处理最高位多余的部分
n -= t * pow(10, i);
}
printf("%lld\n", ans);
return 0;
}
P2596 [ZJOI2006] 书架:(*)文艺平衡树(蓝)
vector 水过。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <vector>
using namespace std;
int n, m;
vector<int> nums;
int main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m;
int x;
for (int i = 1; i <= n; ++i) {cin >> x; nums.push_back(x);}
string op; int s, t;
while (m -- ) {
cin >> op >> s;
if (op == "Top") {
for (int i = 0; i < nums.size(); ++i) {
if (nums[i] == s) {
nums.erase(nums.begin()+i);
break;
}
}
nums.insert(nums.begin(), s);
}
else if (op == "Bottom") {
for (int i = 0; i < nums.size(); ++i) {
if (nums[i] == s) {
nums.erase(nums.begin()+i);
break;
}
}
nums.push_back(s);
}
else if (op == "Insert") {
cin >> t;
int i;
for (i = 0; i < nums.size(); ++i) {
if (nums[i] == s) {
nums.erase(nums.begin()+i);
break;
}
}
nums.insert(nums.begin()+i+t, s);
}
else if (op == "Ask") {
for (int i = 0; i < nums.size(); ++i) {
if (nums[i] == s) {
cout << i << '\n';
break;
}
}
}
else {s --; cout << nums[s] << '\n';}
// for (auto i : nums) cout << i << ' '; cout << '\n';
}
return 0;
}
P5939 [POI1998] 折线:数学,dp(蓝)
题目中 \([-45^{\circ},45^{\circ}]\) 的条件看起来很奇怪,我们可以用一个 trick 来处理:旋转坐标轴。将坐标轴逆时针旋转 \(\theta\),新坐标 \((x',y')\) 满足:
\(\theta=45^{\circ}\) 时,可以都约去 \(\dfrac{\sqrt2}{2}\),则 \(x'=x+y,y'=y-x\)。这时题目变为:折线与 \(x\) 轴夹角 \(\in[0^{\circ}, 90^{\circ}]\)。将所有点按以 \(x'\) 为第一关键字升序排列,以 \(y'\) 为第二关键字降序排列,则答案即为将所有点划分为若干个不下降子序列的最小数量。根据 Dilworth 定理,问题转变为求最长上升子序列长度。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <vector>
using namespace std;
typedef pair<int, int> pii;
const int N = 3e4+10;
int n;
pii pos[N];
vector<int> s;
bool cmp(pii a, pii b) {
if (a.first != b.first) return a.first < b.first;
return a.second > b.second;
}
int main() {
scanf("%d", &n);
int x, y;
for (int i = 1; i <= n; ++i) {
scanf("%d%d", &x, &y);
pos[i] = {x+y, y-x};
}
sort(pos+1, pos+n+1, cmp);
for (int i = 1; i <= n; ++i) {
int p = lower_bound(s.begin(), s.end(), pos[i].second) - s.begin();
if (p == s.size()) s.push_back(pos[i].second);
else s[p] = pos[i].second;
}
printf("%d\n", s.size());
return 0;
}
7.12(Day 3)
SWOJ#1300. 使两数相等:数学(黄)
显然我们只需要考虑 \(a,b\) 的差,那么我们可以把 \(a,b\) 变为 \(0,|a-b|\)。不妨设两个数分别加上 \(x,y\),则
其中,\(i\) 为正整数。
解这个方程,可以得到 \(\left\{\begin{matrix}x=\dfrac{i(i+1)+2|a-b|}{4}\\y=\dfrac{i(i+1)-2|a-b|}{4}\end{matrix}\right.\)。
由于 \(x,y\ge 0\),所以 \(\dfrac{i(i+1)-2|a-b|}{4}\ge 0\),可得 $i\ge \sqrt{2|a-b|+\dfrac{1}{4}}-\dfrac{1}{2} $。注意到 \(i(i+1)-2|a-b|\) 不一定为 \(4\) 的倍数,需要枚举。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
using namespace std;
#define int long long
#define ll double
int t, a, b;
signed main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> t;
while (t -- ) {
cin >> a >> b;
int ans = ceil((sqrt((8*(__int128)abs(a-b)+1)/4.0)) - 1.0/2);
while (((__int128)ans*(ans+1) - 2*abs(a-b)) % 4) ans ++;
cout << ans << '\n';
}
return 0;
}
Codeforces Round 884 (Div. 1 + Div. 2)
CF1844A. Subtraction Game:博弈论,数学(橙)
令 \(n=a+b\),则无论先手取 \(a\) 或 \(b\),后手都必胜。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
int t, a, b;
int main() {
scanf("%d", &t);
while (t -- ) {
scanf("%d%d", &a, &b);
printf("%d\n", a+b);
}
return 0;
}
CF1844B. Permutations & Primes:构造,数学(橙)
若区间 \([l,r]\) 内没有 \(1\),则 \(\text{mex}(a_l,\cdots,a_r)\) 一定为 \(1\)。那么我们需要让有 \(1\) 的区间尽可能多,把 \(1\) 放在中间。
同理,为了让 \(\text{mex}(a_l,\cdots,a_r)\) 为质数,可以把 \(2,3\) 分别放在数列两端。中间的数顺序随意。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 2e5+10;
int t, n, a[N];
int main() {
scanf("%d", &t);
while (t -- ) {
scanf("%d", &n);
if (n == 1) puts("1");
else if (n == 2) puts("2 1");
else {
int idx = 4;
a[1] = 2, a[n] = 3, a[(n+1)/2] = 1;
for (int i = 1; i <= n; ++i) {
if (i == (n+1)/2 || i == 1 || i == n) ;
else a[i] = idx ++;
printf("%d ", a[i]);
}
puts("");
}
}
return 0;
}
CF1844C. Particles:思维(黄)
首先有一个特判:若 \(a_i<0\),则只能留下最大的那个。
接下来考虑存在 \(a_i>0\) 的情况。由于相邻的两个数一定会删去一个,所以最后留下的要么都是奇数项,要么都是偶数项。以奇数项为例:若 \(a_i>0\),则其对答案一定有贡献(可以通过手动模拟发现)。那么答案是奇数项的贡献和偶数项的贡献的最大值。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <queue>
#include <cstring>
using namespace std;
#define int long long
typedef pair<int, int> pii;
const int N = 2e5+10, inf = 2e16;
int t, n, a[N];
signed main() {
scanf("%lld", &t);
while (t -- ) {
scanf("%lld", &n);
bool check = 0;
for (int i = 1; i <= n; ++i) {
scanf("%lld", &a[i]);
if (a[i] > 0) check = 1;
}
if (!check) {
int maxl = -(int)1e16+1;
for (int i = 1; i <= n; ++i) maxl = max(maxl, a[i]);
printf("%lld\n", maxl);
} else {
int odd = 0, even = 0;
for (int i = 1; i <= n; ++i) {
if (i % 2 == 1 && a[i] > 0) odd += a[i];
if (i % 2 == 0 && a[i] > 0) even += a[i];
}
printf("%lld\n", max(odd, even));
}
}
return 0;
}
CF1844D. Row Major:数学,思维,构造(绿)
先给出结论:若 \(c\) 为第一个不能整除 \(n\) 的正整数,则 \(c\) 即为 \(A\) 的循环节。
引理 1:若 \((1\sim d)|n\),则至少需要 \(d+1\) 种字符。
\(d=1\) 时,显然成立。
若 \(d=k-1\) 时成立,则需要 \(k\) 种颜色。\(d=k\) 时,由于 \(k+1\) 与 \(k,k-1,\cdots,1\) 均有连边,所以需要 \(k+1\) 种颜色,得证。
那么 \(c\) 是答案的一个下限,我们只需要证明 \(c\) 的合法性即可。
引理 2:\(c\) 一定可以满足题意。
显然相邻的两项一定不等,我们只需考虑列上的数是否相同。由于 \(c\not\mid k\),所以 \(s_i,s_{i+c},\cdots,s_{i+kc}\) 一定互不相同。得证。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
int t, n;
int main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> t;
while (t -- ) {
cin >> n;
int k = 1;
while (n % k == 0) k ++;
for (int i = 1; i <= n; ++i) cout << (char)('a' + (i-1) % k);
cout << '\n';
}
return 0;
}
CF1844E. Great Grids:图论,搜索(蓝)
根据题目条件,可以知道一个 \(2\times 2\) 的小矩阵中两条对角线上的字母不能都相等。也就是说,如果存在两个约束条件 \((x,y),(x+1,y+1)\) 和 \((x,y+1),(x+1,y)\),则它们不可能同时被满足。
对于一个约束条件 \((x,y),(x+1,y+1)\),我们可以在第 \(x\) 行和第 \(y\) 列之间连一条边权为 \(0\) 的边。对于一个约束条件 \((x,y+1),(x+1,y)\),我们可以在第 \(x\) 行和第 \(y\) 列之间连一条边权为 \(1\) 的边。建完边后,我们用 bfs 搜索判断是否存在矛盾。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <queue>
using namespace std;
typedef pair<int, int> pii;
const int N = 5e4+10;
int t, n, m, k, col[N];
vector<pii> e[N];
void solve() {
scanf("%d%d%d", &n, &m, &k);
for (int i = 1; i <= n+m; ++i) col[i] = -1, e[i].clear();
for (int i = 1; i <= k; ++i) {
int x1, y1, x2, y2; scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
if (y2 == y1+1) e[x1].push_back({n+y1+1, 0}), e[n+y1+1].push_back({x1, 0});
else e[x1].push_back({n+y2+1, 1}), e[n+y2+1].push_back({x1, 1});
}
for (int i = 1; i <= n; ++i) {
if (col[i] != -1) continue;
queue<int> q; q.push(i);
col[i] = 1;
while (!q.empty()) {
int u = q.front(); q.pop();
for (auto edge : e[u]) {
int v = edge.first, w = edge.second;
if (col[v] == -1) {
q.push(v), col[v] = col[u] ^ w;
continue;
} else if (col[v] == col[u] ^ w ^ 1) {
puts("NO");
return ;
}
}
}
}
puts("YES");
return ;
}
int main() {
scanf("%d", &t);
while (t -- ) solve();
return 0;
}
Day 3 模拟赛:
P5322 [BJOI2019] 排兵布阵:dp(绿)
令 \(f_{i,j}\) 表示考虑前 \(i\) 个城堡,总兵数为 \(j\) 的方案数。状态转移方程为:
注意要先将 \(a_{i,k}\) 排序。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 110, M = 20010;
int s, n, m, a[N][N];
int f[N][M];
int main() {
scanf("%d%d%d", &s, &n, &m);
for (int i = 1; i <= s; ++i) {
for (int j = 1; j <= n; ++j)
scanf("%d", &a[j][i]);
}
for (int i = 1; i <= n; ++i) sort(a[i]+1, a[i]+s+1);
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= m; ++j) {
f[i][j] = f[i-1][j];
for (int k = 1; k <= s && 2*a[i][k] < j; ++k)
f[i][j] = max(f[i][j], f[i-1][j-2*a[i][k]-1]+k*i);
}
}
printf("%d\n", f[n][m]);
return 0;
}
CF1119D. Frets On Fire:差分,前缀和,二分(绿)
有一个重要的性质:区间 \([l,r]\) 可以平移为 \([0,r-l]\)。
先将 \(a_i\) 升序排列。令 \(d_i=a_{i+1}-a_i\),则 \(d_i\le r-l+1\) 时,\(a_i\) 和 \(a_{i+1}\) 不会重合。显然这个东西有单调性,再将 \(d_i\) 升序排列,二分查找最后一个 \(d_{pos}\) 满足 \(d_{pos}\le r-l+1\),则询问 \([l,r]\) 的答案为 \(s_{pos}+(r-l+1)(n-pos)\)。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
#define int long long
const int N = 1e5+10;
int n, m, a[N], d[N], s[N];
signed main() {
scanf("%lld", &n);
for (int i = 1; i <= n; ++i) scanf("%lld", &a[i]);
sort(a+1, a+n+1);
for (int i = 1; i < n; ++i) d[i] = a[i+1] - a[i];
sort(d+1, d+n);
for (int i = 1; i < n; ++i) s[i] = s[i-1] + d[i];
int l, r;
scanf("%lld", &m);
while (m -- ) {
scanf("%lld%lld", &l, &r);
int t = r - l + 1, pos = upper_bound(d+1, d+n, t) - d - 1;
printf("%lld ", s[pos]+(n-pos)*t);
}
return 0;
}
P6280 [USACO20OPEN] Exercise G:数学,dp(蓝)
显然奶牛的路径构成一个环,则 \(k=\text{lcm}(len_i)\)。这个不好直接计算,可以枚举 \(k\) 的质因数(均小于 \(n\))。DFS 可以拿到 50 pts。
正解应该是 dp。令 \(f_{i,j}\) 表示用前 \(i\) 个质数(一定用第 \(i\) 个),构成环的总长度为 \(j\) 的 \(\sum k\)。初始状态为 \(f_{0,0}=1\),答案为 \(\sum f_{i,n}\)。
状态转移方程为:
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
using namespace std;
typedef long long ll;
const int N = 1e4+10;
int n, m, ans = 1;
int f[1500][N];
int prime[N], cnt;
bool st[N];
int power(int a, int b, int p) {
int ans = 1;
while (b) {
if (b & 1) ans = (ll)ans * a % p;
a = (ll)a * a % p;
b >>= 1;
}
return ans;
}
void Euler(int n) {
st[1] = 1;
for (int i = 2; i <= n; ++i) {
if (!st[i]) prime[++ cnt] = i;
for (int j = 1; prime[j] <= n/i && j <= cnt; ++j) {
st[i*prime[j]] = 1;
if (i % prime[j] == 0) break;
}
}
}
int main() {
scanf("%d%d", &n, &m);
Euler(n);
f[0][0] = 1;
for (int i = 1; i <= cnt; ++i) {
for (int j = 0; j <= n; ++j) {
f[i][j] = f[i-1][j];
for (int t = prime[i]; t <= j; t *= prime[i])
f[i][j] = (f[i][j] + (ll)f[i-1][j-t] * t % m) % m;
}
}
for (int i = 1; i <= n; ++i) ans = (ans + f[cnt][i]) % m;
printf("%d\n", ans);
return 0;
}
P2286 [HNOI2004] 宠物收养场:平衡树,STL(蓝)
老师老师,我会写平衡树!做完了。
老师老师,我会用 set!做完了。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <set>
using namespace std;
typedef set<int>::iterator it;
const int P = 1e6, inf = 1e9;
int n, c, p, ans;
set<int> cats, people;
int main() {
cats.insert(inf), cats.insert(-inf);
people.insert(inf), people.insert(-inf);
scanf("%d", &n);
int op, x;
while (n -- ) {
scanf("%d%d", &op, &x);
if (!op) {
if (!c && p) {
it suf = people.lower_bound(x), pre = -- suf; suf ++;
if (x - *pre <= *suf - x) {
ans += x - *pre;
people.erase(pre);
} else {
ans += *suf - x;
people.erase(suf);
}
p --;
} else c ++, cats.insert(x);
} else {
if (c) {
it suf = cats.lower_bound(x), pre = -- suf; suf ++;
if (x - *pre <= *suf - x) {
ans += x - *pre;
cats.erase(pre);
} else {
ans += *suf - x;
cats.erase(suf);
}
c --;
} else p ++, people.insert(x);
}
ans %= P;
}
printf("%d\n", ans);
return 0;
}
7.13(Day 4)
HDU2089. 不要62:数位 dp(蓝)
详见注释。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
using namespace std;
int n, m;
int f[8][10]; // f[i][j]表示以j为开头,位数为i的合法答案
void init() {
int now = 9; // now 表示 f[i-1][j] 的和
for (int i = 0; i <= 9; ++i) f[1][i] = (i == 4) ? 0 : 1;
for (int i = 2; i <= 7; ++i) {
int tmp = 0;
for (int j = 0; j <= 9; ++j) {
if (j == 4) continue; // 不能包含 4
else if (j == 6) f[i][j] = now - f[i-1][2]; // 如果当前最高位是6,后一位就不能为2
else f[i][j] = now;
tmp += f[i][j];
}
now = tmp;
}
}
int get(int n) {
int ans = 0, last = 0; // last 表示上一位
for (int i = log10(n); i >= 0; --i) { // 从高位向低位枚举
int t = n / (int)pow(10, i); // 取出当前位
for (int j = 0; j < t; ++j) {
if ((last == 6) && j == 2) continue;
ans += f[i+1][j];
}
if ((t == 4) || (t == 2 && last == 6)) break; // 后面的答案都无法做出贡献
last = t, n -= t * pow(10, i);
}
return ans;
}
int main() {
init();
while (~scanf("%d%d", &n, &m)) {
if (!n && !m) break;
printf("%d\n", get(m+1)-get(n));
}
return 0;
}
P4161 [SCOI2009] 游戏:数学,dp(蓝)
昨天 T3 的双倍经验,但是统计的是数量。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, ans, f[N];
int cnt, prime[N];
bool st[N];
void Euler(int n) {
st[1] = 1;
for (int i = 2; i <= n; ++i) {
if (!st[i]) prime[++ cnt] = i;
for (int j = 1; prime[j] <= n/i && j <= cnt; ++j) {
st[i*prime[j]] = 1;
if (i % prime[j] == 0) break;
}
}
}
int main() {
scanf("%d", &n);
Euler(n);
f[0] = 1;
for (int i = 1; i <= cnt; ++i) {
for (int j = n; j >= prime[i]; --j) {
for (int k = prime[i]; k <= j; k *= prime[i])
f[j] += f[j-k];
}
}
for (int i = 0; i <= n; ++i) ans += f[i];
printf("%d\n", ans);
return 0;
}
P2949 [USACO09OPEN] Work Scheduling G:反悔贪心(绿)
将所有工作按截止时间排序,用一个小根堆存储当前完成的工作的价值。对于一个工作 \((t,v)\),若 \(t<\) 小根堆内元素个数,说明在截止前仍然可以完成该工作;否则从小根堆中取出最小值,判断其能否替换。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <queue>
using namespace std;
#define int long long
typedef pair<int, int> pii;
const int N = 1e5+10;
int n, ans; pii work[N];
priority_queue<int, vector<int>, greater<int>> q;
signed main() {
scanf("%lld", &n);
for (int i = 1; i <= n; ++i) {
int t, v; scanf("%lld%lld", &t, &v);
work[i] = {t, v};
}
sort(work+1, work+n+1);
for (int i = 1; i <= n; ++i) {
int t = work[i].first, v = work[i].second;
if (t <= q.size()) {
int u = q.top();
if (v > u) q.pop(), q.push(v), ans += v-u;
else continue;
} else {
q.push(v), ans += v;
}
}
printf("%lld\n", ans);
return 0;
}
P4053 [JSOI2007] 建筑抢修:反悔贪心(蓝)
先按截止时间排序。大根堆存储施工建筑所需的时间,若时间不够则取出堆头,判断是否更优。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <queue>
using namespace std;
#define int long long
typedef pair<int, int> pii;
const int N = 1.5e5+10;
int n, tot, ans; pii build[N];
priority_queue<int, vector<int>> q;
signed main() {
scanf("%lld", &n);
int last, line;
for (int i = 1; i <= n; ++i) {
scanf("%lld%lld", &last, &line);
build[i] = {line, last};
}
sort(build+1, build+n+1);
for (int i = 1; i <= n; ++i) {
last = build[i].second, line = build[i].first;
if (last + tot > line) {
int t = q.top();
if (t > last) q.pop(), q.push(last), tot += last-t;
else continue;
} else {
q.push(last);
ans ++, tot += last;
}
}
printf("%lld\n", ans);
return 0;
}
P2107 小Z的AK计划:反悔贪心(蓝)
显然应该一直从左往右走,按 \(x\) 坐标升序排列。然后转化为上面的模型。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <queue>
using namespace std;
#define int long long
typedef pair<int, int> pii;
const int N = 1e5+10;
int n, m, tot, last; pii test[N];
priority_queue<int, vector<int>> q;
signed main() {
scanf("%lld%lld", &n, &m);
int pos, time;
for (int i = 1; i <= n; ++i) {
scanf("%lld%lld", &pos, &time);
test[i] = {pos, time};
}
sort(test+1, test+n+1);
for (int i = 1; i <= n; ++i) {
pos = test[i].first, time = test[i].second;
if (tot+pos-last > m) {
auto t = q.top();
if (time+pos-last < t) q.pop(), q.push(time), tot += pos-last+time-t, last = pos;
else continue;
} else {
q.push(time);
tot += pos-last+time, last = pos;
}
}
printf("%lld\n", q.size());
return 0;
}
Day4 模拟赛:
P3147 [USACO16OPEN] 262144 P:区间 dp(绿)(弱化版:P3146 [USACO16OPEN] 248 G)
令 \(f_{i,j}\) 表示以 \(i\) 为区间左端点,合成的数为 \(j\) 时的右端点位置。初始时 \(f_{i,a_i}=i\)。
状态转移方程:
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 3e5+10, M = 60;
int n, ans, a[N];
int f[N][M]; // f[i][j]表示以i为左端点,最终合成j的区间长度
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) {
scanf("%d", &a[i]);
f[i][a[i]] = i;
}
for (int j = 1; j <= 58; ++j) {
for (int i = 1; i <= n; ++i) {
if (f[i][j-1]) f[i][j] = f[f[i][j-1]+1][j-1];
if (f[i][j]) ans = j;
}
}
printf("%d\n", ans);
return 0;
}
P3010 [USACO11JAN] Dividing the Gold S:01 背包(绿)
看起来不太好搞,实际上就是 01 背包判断可行性和方案数。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 6e5+10, P = 1e6;
int n, sum;
int a[N], f[N], g[N];
int ans;
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%d", &a[i]), sum += a[i];
f[0] = 1, g[0] = 1;
sort(a+1, a+n+1);
for (int i = 1; i <= n; ++i) {
for (int j = sum; j >= a[i]; --j) {
f[j] |= f[j-a[i]], g[j] += g[j-a[i]], g[j] %= P;
if (f[j] && abs(j*2-sum) < abs(ans*2-sum)) ans = j;
}
}
// for (int j = 0; j <= sum; ++j) printf("f[%d]=%d, g[%d]=%d\n", j, f[j], j, g[j]);
printf("%d\n%d\n", abs(2*ans-sum), g[ans]);
return 0;
}
P3049 [USACO12MAR] Landscaping S:反悔贪心(绿)(*加强版 P2748 [USACO16OPEN] Landscaping P)
令 \(c_i=a_i-b_i\)。以 \(c_i>0\) 的情况为例,令 \(v_i\) 表示当前从第 \(i\) 个数中移走一个单位的最小花费。我们有两种选择:
- 直接移走,花费为 \(x\);
- 补到第 \(j\;(i>j)\) 个数里,花费为 \(z|i-j|=zi-zj\),还要减去之前的贡献 \(v_j\)。
那么有 \(v_i=\min(x,zi-zj-v_j)=\min(x,zi+(-zj-v_j))\)。
根据反悔贪心的思想,我们需要让 \(v_i\) 最小,就要让 \(-zj-v_j\) 尽可能小。可以分别用两个小根堆维护 \(c_i>0\) 和 \(c_i<0\) 的 \(-zj-v_j\)。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <queue>
using namespace std;
#define int long long
const int N = 1e5+10;
priority_queue<int, vector<int>, greater<int>> neg, pos;
int n, x, y, z, ans, num[N];
signed main() {
scanf("%lld%lld%lld%lld", &n, &x, &y, &z);
for (int i = 1; i <= n; ++i) {
int a, b; scanf("%lld%lld", &a, &b);
num[i] = a-b;
}
for (int i = 1; i <= n; ++i) {
if (num[i] < 0) {
for (int j = 1; j <= -num[i]; ++j) {
int v = x;
if (pos.size() > 0) v = min(v, z*i+pos.top()), pos.pop();
neg.push({-z*i-v});
ans += v;
}
} else {
for (int j = 1; j <= num[i]; ++j) {
int v = y;
if (neg.size() > 0) v = min(v, z*i+neg.top()), neg.pop();
pos.push({-z*i-v});
ans += v;
}
}
}
printf("%lld\n", ans);
return 0;
}
P1110 [ZJOI2007] 报表统计:平衡树(蓝)
直接用 set 模拟即可。注意 set 中一个数只能出现一次,由于 MIN_GAP 需要删除,所以需要用一个 pair 来存储它们的值和位置。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <set>
using namespace std;
typedef pair<int, int> pii;
typedef set<int>::iterator it;
typedef set<pii>::iterator itp;
const int N = 5e5+10, inf = 1e9;
int n, m, a[N], b[N];
int idx, L[N], R[N];
set<pii> Gap; set<int> Nums, Sort_Gap;
int main() {
// ios::sync_with_stdio(0);
// cin.tie(0), cout.tie(0);
Nums.insert(-inf), Nums.insert(inf);
cin >> n >> m;
for (int i = 1; i <= n; ++i) {
cin >> a[i]; b[i] = a[i]; L[i] = R[i] = ++ idx;
if (i > 1) Gap.insert({abs(a[i]-a[i-1]), L[i]});
it suf = Nums.lower_bound(a[i]), pre = -- suf; suf ++;
Sort_Gap.insert(min(abs(*suf-a[i]), abs(a[i]-*pre)));
Nums.insert(a[i]);
}
// for (auto i : Gap) cout << i.first << ' ' << i.second << " / "; cout << '\n';
string op; int i, k;
while (m -- ) {
cin >> op;
if (op == "INSERT") {
cin >> i >> k;
if (i < n) Gap.erase({abs(b[i]-a[i+1]), L[i+1]});
Gap.insert({abs(k-b[i]), R[i]});
if (i < n) Gap.insert({abs(a[i+1]-k), L[i+1]});
b[i] = k;
it suf = Nums.lower_bound(k), pre = -- suf; suf ++;
Sort_Gap.insert(min(abs(*suf-k), abs(k-*pre)));
Nums.insert(k);
} else if (op == "MIN_GAP") {
cout << (*Gap.begin()).first << '\n';
} else {
cout << *Sort_Gap.begin() << '\n';
}
// for (auto i : Gap) cout << i.first << ' ' << i.second << " / "; cout << '\n';
}
return 0;
}
7.14(Day 5)
P1503 鬼子进村:树状数据结构(蓝)
set 维护删去的数并二分查找。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <vector>
#include <set>
using namespace std;
const int N = 5e4+10;
int n, m;
int idx, stack[N];
set<int> Del;
int main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m;
char op; int x;
Del.insert(0), Del.insert(n+1);
while (m -- ) {
cin >> op;
if (op == 'D') {
cin >> x;
stack[++ idx] = x, Del.insert(x);
} else if (op == 'R') {
int t = stack[idx --]; Del.erase(t);
} else {
cin >> x;
auto suf = Del.lower_bound(x), pre = -- suf; suf ++;
if (*suf == x) cout << 0 << '\n';
else cout << (*suf) - (*pre) - 1 << '\n';
}
}
return 0;
}
P3850 [TJOI2007] 书架:平衡树(紫)
直接用 vector 存储 string 会超时,需要映射。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <vector>
#include <unordered_map>
using namespace std;
int n, m, q, idx; string s;
vector<int> S;
unordered_map<int, string> Map;
int main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n;
while (n -- ) {cin >> s; S.push_back(++ idx), Map[idx] = s;}
int pos;
cin >> m;
while (m -- ) {cin >> s >> pos; S.insert(S.begin()+pos, ++ idx), Map[idx] = s;}
cin >> q;
while (q -- ) {cin >> pos; cout << Map[S[pos]] << '\n';}
return 0;
}
SP19568. PRMQUER - Prime queries:珂朵莉树,线段树(紫)
接近板子。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <set>
using namespace std;
const int N = 1e7+10;
int n, m;
int prime[N], cnt;
bool st[N];
struct Node {
int l, r; mutable int v;
Node (int l, int r = 0, int v = 0) : l(l), r(r), v(v) {}
bool operator < (const Node &T) const {
return l < T.l;
}
};
set<Node> s;
typedef set<Node>::iterator iter;
iter split(int pos) {
iter it = s.lower_bound(Node(pos));
if (it != s.end() && it->l == pos) return it;
it --;
if (it->r < pos) return s.end();
int l = it->l, r = it->r, v = it->v;
s.erase(it), s.insert(Node(l, pos-1, v));
return s.insert(Node(pos, r, v)).first;
}
void assign(int l, int r, int x) {
iter itr = split(r+1), itl = split(l);
s.erase(itl, itr);
s.insert(Node(l, r, x));
}
int query(int l, int r) {
int ans = 0;
iter itr = split(r+1), itl = split(l);
for (iter it = itl; it != itr; ++it) {
int l = it->l, r = it->r, v = it->v;
if (v <= (int)(1e7) && !st[v]) ans += r-l+1;
}
return ans;
}
void Euler(int n) {
st[1] = 1;
for (int i = 2; i <= n; ++i) {
if (!st[i]) prime[++ cnt] = i;
for (int j = 1; prime[j] <= n/i && j <= cnt; ++j) {
st[i*prime[j]] = 1;
if (i % prime[j] == 0) break;
}
}
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m;
Euler((int)(1e7));
int x;
for (int i = 1; i <= n; ++i) {cin >> x; s.insert(Node(i, i, x));}
char op; int l, r, v;
while (m -- ) {
cin >> op;
if (op == 'A') {
cin >> v >> l;
split(l+1); iter it = split(l); int k = it->v;
s.erase(it), s.insert(Node(l, l, v+k));
} else if (op == 'R') {
cin >> v >> l >> r;
assign(l, r, v);
} else {
cin >> l >> r;
cout << query(l, r) << '\n';
}
}
return 0;
}
CF1638E Colorful Operations:(*)线段树,珂朵莉树(紫)
对于操作 \(1\),显然就是珂朵莉树的区间推平操作。
对于操作 \(2\),我们直接用一个桶维护每个颜色的增加量 \(tag_c\)。
对于操作 \(3\),显然就是 \(a_i+tag_{col_i}\)。
接下来考虑区间推平对 \(a_i\) 的影响。显然要先加上 \(tag_{col_i}\),为了不计算变化后的颜色 \(col_i'\) 之前的的增加量,还需要再减去 \(tag_{col_i'}\)。
所以用线段树维护单点值,并支持区间修改;珂朵莉树维护颜色段。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <set>
using namespace std;
#define int long long
const int N = 1e6+10;
int n, m, col[N];
struct CthNode {
int l, r; mutable int v;
CthNode (int l, int r = 0, int v = 0) : l(l), r(r), v(v) {}
bool operator < (const CthNode &T) const {
return l < T.l;
}
};
set<CthNode> s;
typedef set<CthNode>::iterator iter;
iter split(int pos) {
iter it = s.lower_bound(CthNode(pos));
if (it != s.end() && it->l == pos) return it;
it --;
if (it->r < pos) return s.end();
int l = it->l, r = it->r, v = it->v;
s.erase(it), s.insert(CthNode(l, pos-1, v));
return s.insert(CthNode(pos, r, v)).first;
}
void assign(int l, int r, int x) {
iter itr = split(r+1), itl = split(l);
s.erase(itl, itr), s.insert(CthNode(l, r, x));
}
struct SegNode {
int l, r, sum, add;
} seg[N<<2];
void Pushdown(SegNode &u, SegNode &fa) {
u.sum += (u.r - u.l + 1) * fa.add, u.add += fa.add;
}
void pushdown(int u) {
if (seg[u].add) {
Pushdown(seg[u<<1], seg[u]), Pushdown(seg[u<<1|1], seg[u]);
seg[u].add = 0;
}
}
void build(int u, int l, int r) {
seg[u].l = l, seg[u].r = r;
if (l == r) return ;
int mid = l + r >> 1;
build(u<<1, l, mid), build(u<<1|1, mid+1, r);
}
int query(int u, int pos) {
if (seg[u].l == pos && seg[u].r == pos) return seg[u].sum;
pushdown(u);
int mid = seg[u].l + seg[u].r >> 1;
if (pos <= mid) return query(u<<1, pos);
else return query(u<<1|1, pos);
}
void modify(int u, int l, int r, int v) {
if (seg[u].l >= l && seg[u].r <= r) {SegNode t; t.add = v, Pushdown(seg[u], t); return ;}
pushdown(u);
int mid = seg[u].l + seg[u].r >> 1;
if (l <= mid) modify(u<<1, l, r, v);
if (r > mid) modify(u<<1|1, l, r, v);
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m; build(1, 1, n), s.insert(CthNode(1, n, 1));
string op; int l, r, c;
while (m -- ) {
cin >> op;
if (op == "Color") {
cin >> l >> r >> c;
iter itr = split(r+1), itl = split(l);
for (iter it = itl; it != itr; ++it) {
int l = it->l, r = it->r, v = it->v;
modify(1, l, r, col[v]-col[c]);
}
assign(l, r, c);
} else if (op == "Add") {
cin >> c >> l; col[c] += l;
} else {
cin >> l;
split(l+1); iter it = split(l);
cout << query(1, l) + col[it->v] << '\n';
}
}
return 0;
}
P9455 [入门赛 #14] 塔台超频 (Hard Version):二分(绿)
正解是 \(O(n\log V)\) 的,但是我还多带了一个 \(\log n\) 跳右端点。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <queue>
using namespace std;
typedef pair<int, int> pii;
const int N = 5e5+10;
int n, a[N], b[N], f[N];
bool check(int x) {
int maxr = 1;
for (int i = 1; i <= maxr; ++i) {
int t = upper_bound(a+1, a+n+1, a[i]+b[i]+x)-a-1;
maxr = max(maxr, t);
if (maxr >= n) return 1;
}
return 0;
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%d%d", &a[i], &b[i]);
int l = 0, r = a[n]-a[1];
while (l < r) {
int mid = l + r >> 1;
if (check(mid)) r = mid;
else l = mid+1;
}
printf("%d\n", l);
return 0;
}
P9456 [入门赛 #14] Three-View Projection (Hard Version):模拟(黄)
对着样例找下规律就好了。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 210;
int n, m, t;
int a[N][N][N], x[N][N], y[N][N], z[N][N];
int main() {
scanf("%d%d%d", &n, &m, &t);
for (int i = 1; i <= t; ++i) {
for (int j = 1; j <= n; ++j)
for (int k = 1; k <= m; ++k) {
scanf("%d", &a[i][j][k]);
x[i][j] |= a[i][j][k], y[i][k] |= a[i][j][k], z[k][j] |= a[i][j][k];
}
}
for (int i = t; i >= 1; --i) {
for (int j = 1; j <= n; ++j)
printf("%d " , x[i][j]);
puts("");
}
for (int i = t; i >= 1; --i) {
for (int j = m; j >= 1; --j)
printf("%d ", y[i][j]);
puts("");
}
for (int i = m; i >= 1; --i) {
for (int j = 1; j <= n; ++j)
printf("%d ", z[i][j]);
puts("");
}
return 0;
}
Day 5 模拟赛:
P3054 [USACO12OPEN] Running Laps S:(*)数学,平衡树/树状数组(绿)
将 \(v_i\) 升序排列,则此时速度最快的人是 \(v_n\)。第 \(n\) 个人可以跑 \(l\) 圈,则第 \(i\) 个人可以跑 \(num_i=\dfrac{v_i}{v_n}\cdot l\) 圈,最后一圈跑了 \(dis_i=\dfrac{v_i\cdot l\bmod v_n}{v_n}\) 圈。由于所有人多余的部分都有 \(v_n\),所以可以都乘上 \(v_n\)。
那么第 \(i\) 个人对答案的贡献即为 \(i\cdot num_i-\displaystyle\sum_{1\le j\le i}num_i-x\),其中 \(x\) 表示 \(\forall\;1\le j\le i\),满足 \(dis_i<dis_j\) 的数量。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#define int long long
using namespace std;
const int N = 1e6+10;
int n, l, t, ans, v[N];
int a[N], s[N], dis[N];
int c[N];
int lowbit(int x) {
return x & -x;
}
void add(int pos, int x) {
for (int i = pos; i < N; i += lowbit(i))
c[i] += x;
}
int query(int pos) {
int sum = 0;
for (int i = pos; i > 0; i -= lowbit(i))
sum += c[i];
return sum;
}
signed main() {
scanf("%lld%lld%lld", &n, &l, &t);
for (int i = 1; i <= n; ++i) scanf("%lld", &v[i]);
sort(v+1, v+n+1);
for (int i = 1; i <= n; ++i) {
a[i] = v[i]*l/v[n], s[i] = s[i-1]+a[i], dis[i] = v[i]*l%v[n];
ans += i * a[i] - s[i] - ((i-1)-query(dis[i]+1));
add(dis[i]+1, 1);
}
printf("%lld\n", ans);
return 0;
}
U312355 缺席的商人:(*)01 背包(绿)
令 \(f_{i,j}\) 表示考虑第 \(1\sim i\) 个物品,容量为 \(j\) 的最大价值,\(g_{i,j}\) 表示考虑第 \(i\sim n\) 个物品,容量为 \(j\) 的最大价值。显然这两个可以通过 01 背包求出。那么若第 \(k\) 个商人没来,最大价值即为 \(\max_{1\le i\le n}\{f_{k-1,i}+g_{k+1,i}\}\)。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 1010, M = 5010;
int n, m, t, w[N], v[N];
int f[N][M], g[N][M];
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++i) scanf("%d%d", &w[i], &v[i]);
for (int i = 1; i <= n; ++i) {
for (int j = 0; j <= m; ++j) {
f[i][j] = f[i-1][j];
if (j >= v[i]) f[i][j] = max(f[i][j], f[i-1][j-v[i]]+w[i]);
}
}
for (int i = n; i >= 1; --i) {
for (int j = 0; j <= m; ++j) {
g[i][j] = g[i+1][j];
if (j >= v[i]) g[i][j] = max(g[i][j], g[i+1][j-v[i]]+w[i]);
}
}
scanf("%d", &t);
while (t -- ) {
int k; scanf("%d", &k);
int ans = 0;
for (int i = 0; i <= m; ++i) ans = max(ans, f[k-1][i]+g[k+1][m-i]);
printf("%d\n", ans);
}
return 0;
}
P3628 [APIO2010] 特别行动队:(*)斜率优化 dp(紫)
令 \(f_i\) 表示考虑前 \(i\) 个节点的最大战斗力,\(s_i\) 表示 \(x_i\) 的前缀和,则状态转移方程为:
假设 \(f_i\) 可以从 \(f_j\) 转换而来,将其转换为一次函数的形式,可以得到:
此时 \(f_j+as_j^2-bs_j\) 为纵坐标 \(x\),\(s_i\) 为横坐标 \(y\),\(2a\) 为斜率 \(k_i\),\(-as_i^2-bs_i-c+f_i\) 为截距 \(b_i\)。那么要使 \(f_i\) 最大,就要使 \(b\) 最大。由于 \(a\le -1,x_i>0\),所以 \(k_i\) 单调递减,\(y\) 也单调递减,\(x\) 单调递增。画图可以发现我们需要维护一个上凸壳的右半部分,满足对于凸壳内的相邻点 \(j_1<j_2<j_3\),都有 \(k_{j_1,j_2}>k_{j_2,j_3}\)。
对于一个最优斜率 \(k_i\),其应满足 \(k_{j_1,j_2}\ge k_j>k_{j_2,j_3}\)。那么我们需要用一个单调队列维护。
实现细节还是挺多的。
点击查看代码
#include <iostream>
#include <cstdio>
#include <deque>
using namespace std;
#define int long long
const int N = 1e6+10;
int n, a, b, c, s[N], f[N];
deque<int> nums; // 维护上凸壳
int get_y(int pos) {
return f[pos] + a * s[pos] * s[pos] - b * s[pos];
}
signed main() {
scanf("%lld%lld%lld%lld", &n, &a, &b, &c);
for (int i = 1;i <= n; ++i) scanf("%lld", &s[i]), s[i] += s[i-1];
nums.push_back(0);
for (int i = 1; i <= n; ++i) {
while (nums.size() > 1 &&
(get_y(nums[0]) - get_y(nums[1]) < (2*a*s[i] * (s[nums[0]]-s[nums[1]]))))
nums.pop_front();
int j = nums[0]; f[i] = f[j] + a*(s[i]-s[j])*(s[i]-s[j]) + b*(s[i]-s[j]) + c;
int t = nums.size()-1;
while (nums.size() > 1 &&
(get_y(nums[t-1])-get_y(nums[t]))*(s[nums[t]]-s[i]) < (get_y(nums[t])-get_y(i))*(s[nums[t-1]]-s[nums[t]]))
nums.pop_back(), t --;
nums.push_back(i);
}
printf("%lld\n", f[n]);
return 0;
}
P5838 [USACO19DEC] Milk Visits G:树链剖分,分块,可持久化线段树(紫)
树链剖分将重链转化为连续序列,对这个序列分块,存储每一种颜色是否在块内出现过。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <vector>
#include <cmath>
using namespace std;
const int N = 1e5+10;
int n, m, p, T[N];
int idx, id[N], w[N];
int dep[N], f[N], son[N], top[N], size[N];
vector<int> e[N];
void get_son(int u, int fa) {
dep[u] = dep[fa]+1, f[u] = fa, size[u] = 1;
for (auto v : e[u]) {
if (v == fa) continue;
get_son(v, u), size[u] += size[v];
if (size[v] > size[son[u]]) son[u] = v;
}
}
void get_top(int u, int t) {
top[u] = t, id[u] = ++ idx, w[idx] = T[u];
if (son[u]) get_top(son[u], t);
for (auto v : e[u]) {
if (v == f[u] || v == son[u]) continue;
get_top(v, v);
}
}
int block[N], L[N], R[N];
bool col[350][N];
void init_block() {
p = sqrt(n);
for (int i = 1; i <= n; ++i) {
block[i] = (i+p-1) / p, L[i] = (block[i]-1)*p+1, R[i] = min(n, block[i]*p);
col[block[i]][w[i]] = 1;
}
}
bool find(int l, int r, int c) { // 查找区间[l,r]内是否存在 c
if (block[r]-block[l] < 2) {
for (int i = l; i <= r; ++i) {
if (w[i] == c)
return 1;
}
return 0;
}
for (int i = l; i <= R[l]; ++i) {
if (w[i] == c)
return 1;
}
for (int i = block[l]+1; i <= block[r]-1; ++i) {
if (col[i][c])
return 1;
}
for (int i = L[r]; i <= r; ++i) {
if (w[i] == c)
return 1;
}
return 0;
}
bool query(int u, int v, int c) {
while (top[u] != top[v]) {
if (dep[top[u]] < dep[top[v]]) swap(u, v);
if (find(id[top[u]], id[u], c)) return 1;
u = f[top[u]];
}
if (dep[u] > dep[v]) swap(u, v);
return find(id[u], id[v], c);
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++i) scanf("%d", &T[i]);
for (int i = 1; i < n; ++i) {
int u, v; scanf("%d%d", &u, &v);
e[u].push_back(v), e[v].push_back(u);
}
get_son(1, 1), get_top(1, 1);
init_block();
for (int i = 1; i <= m; ++i) {
int u, v, c; scanf("%d%d%d", &u, &v, &c);
printf("%d", query(u, v, c));
}
return 0;
}
7.15(Day 6)
开始学斜率优化。
AcWing 300. 任务安排1:费用提前计算优化 dp(绿+)
令 \(f_{i,j}\) 表示完成前 \(i\) 个任务,第 \(i\) 个任务为第 \(j\) 组任务最后一个时的费用最小值。则状态转移方程为:
其中,\(k\) 表示上一组任务的最后一个任务,\(j\cdot S+\sum_{p = 1}^i T_i\) 表示该任务的结束时间(分为 \(j\) 组任务,需要启动 \(j\) 次,再加上当前所有任务的基础时间),\(\sum_{p=k+1}^iC_i\) 表示该组任务的费用系数之和。
但这样做的时间复杂度是 \(O(n^3)\)。注意到在 dp 的过程中,为了计算 \(S\) 对一组任务 \([l,r]\) 的贡献,我们人为地引入了参数 \(j\)。这里我们可以引用一个思想:费用提前计算。由于一组任务 \([l,r]\) 的启动时间 \(S\) 会影响的任务为 \([l,n]\),我们可以直接把 \([l,n]\) 中的这个 \(S\) 直接累加到当前状态上计算。令 \(f_i\) 表示完成前 \(i\) 个任务的费用最小值,则状态转移方程为:
其中的 \(S\left ( \sum_{p=i+1}^nC_i \right )\) 即为提前计算的量。可以用前缀和优化,时间复杂度 \(O(n^2)\)。
由于我们采用了费用提前计算,所以这里只有 \(f_n\) 的答案是正确的。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
#define int long long
const int N = 5010;
int n, s, t[N], c[N], sumt[N], sumc[N];
int f[N];
signed main() {
memset(f, 0x3f, sizeof f);
scanf("%lld%lld", &n, &s);
for (int i = 1; i <= n; ++i)
scanf("%lld%lld", &t[i], &c[i]), sumt[i] = sumt[i-1]+t[i], sumc[i] = sumc[i-1]+c[i];
f[0] = 0;
for (int i = 1; i <= n; ++i) {
for (int j = 0; j < i; ++j)
f[i] = min(f[i], f[j]+s*(sumc[n]-sumc[j])+sumt[i]*(sumc[i]-sumc[j]));
}
printf("%lld\n", f[n]);
return 0;
}
AcWing 301. 任务安排2:斜率优化 dp,单调队列(蓝)
为了简化公式,我们令 \(sumT_i,sumC_i\) 分别表示 \(T_i,C_i\) 的前缀和。
假设我们可以从 \(f_j\) 推到 \(f_i\)。则有:
我们将 \(f_j,sumC_j\) 视作未知量,将其他均视为已知量,则上式可变形为:
可以将这个式子看作一个一次函数 \(y=k_ix+b_i\),其中 \(k_i=S+sumT_i\),\(b_i=f_i-S\cdot sumC_n-sumT_i\cdot sumC_i\)。显然 \(b_i\) 最小时 \(f_i\) 最小。

以 \(sumC\) 为横坐标,\(f\) 为纵坐标建立平面直角坐标系。假设存在三个点 \(j_1<j_2<j_3\),由于 \(T_i,C_i\) 都是正数,所以 \(sumT_i,sumC_i,f_j\) 单调递增,即 \(x_j,y_j\) 都单调递增。若线段 \((j_1,j_2)\) 和 \((j_2,j_3)\) 构成一个上凸壳,则 \(j_2\) 一定不能成为最优解。
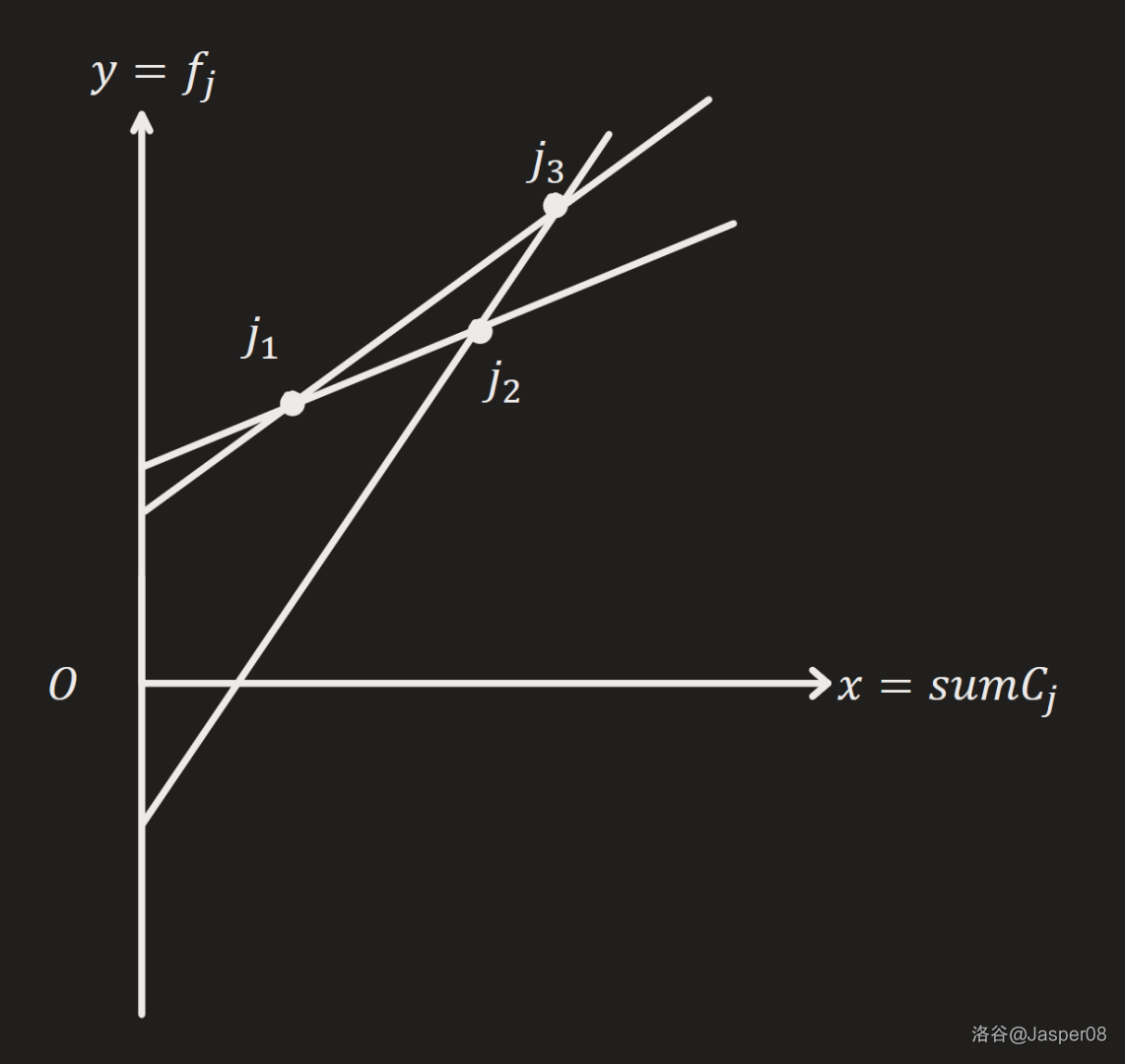
若线段 \((j_1,j_2)\) 和 \((j_2,j_3)\) 构成一个下凸壳,则 \(j_2\) 有可能成为最优解。那么,\(j_2\) 有可能成为最优决策,当且仅当 \(k_{j_1,j_2}<k_{j_2,j_3}\),即:
考虑如何计算答案:

可以看到,对于一个下凸壳的最优斜率 \(k_i\),一定有 \(k_{j_1,j_2}\le k_i<k_{j_2,j_3}\)。此时 \(j_2\) 即为最优决策。
综上,我们需要维护点构成的下凸壳,可以使用单调队列维护(单调队列内相邻两点连接构成的直线 \(k\) 单调递增)。我们需要维护队头 \(h\) 满足 \(k_{h,h}\le k_i<k_{h,h+1}\),每次取出 \(j=h\),将其带入状态转移方程计算即可。将 \(i\) 加入单调队列时,我们需要维护队尾 \(t\) 满足 \(k_{t-1,t}\le k_{t,i}\)。
时间复杂度 \(O(n)\)。注意除法计算 \(k\) 容易爆精度,需要交叉相乘。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <deque>
using namespace std;
#define int long long
const int N = 3e5+10;
int n, s, t[N], c[N], sumt[N], sumc[N];
int f[N];
deque<int> nums; // 维护下凸壳中的有效点
signed main() {
scanf("%lld%lld", &n, &s);
for (int i = 1; i <= n; ++i)
scanf("%lld%lld", &t[i], &c[i]), sumt[i] = sumt[i-1]+t[i], sumc[i] = sumc[i-1]+c[i];
nums.push_back(0), nums.push_back(0);
for (int i = 1; i <= n; ++i) {
int nowk = s+sumt[i];
while (nums.size() > 1 &&
(f[nums[1]]-f[nums[0]] <= nowk*(sumc[nums[1]]-sumc[nums[0]])))
nums.pop_front();
int j = nums[0]; f[i] = f[j] + s*(sumc[n]-sumc[j]) + sumt[i] * (sumc[i]-sumc[j]);
int t = nums.size()-1;
while (nums.size() > 1 &&
((f[i]-f[nums[t]])*(sumc[nums[t]]-sumc[nums[t-1]]) < (f[nums[t]]-f[nums[t-1]])*(sumc[i]-sumc[nums[t]])))
nums.pop_back(), t --;
nums.push_back(i);
}
printf("%lld\n", f[n]);
return 0;
}
Day 6 模拟赛:
U312891 快递:dfs,思维(绿)
从 \(0\) 号节点 dfs 更新能够到达点 \(u\) 的出发时间 \([l_u,r_u]\)。那么有 \(l_u=\max(l_{fa_u}+w_i,s_i)\),\(r_u=\min(r_{fa_u}+w_i,e_i)\)。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
#define int long long
const int N = 5e5+10;
int n, m;
int l[N], r[N];
int idx, h[N], e[N], ne[N], c[N], s[N], t[N];
void add(int u, int v, int w, int x, int y) {
e[++ idx] = v, ne[idx] = h[u], c[idx] = w, s[idx] = x, t[idx] = y, h[u] = idx;
}
void dfs(int u, int fa, int dis) {
for (int i = h[u]; i != -1; i = ne[i]) {
int v = e[i]; if (v == fa) continue;
l[v] = max(l[u], s[i]-dis), r[v] = min(r[u], t[i]-dis), dfs(v, u, dis+c[i]);
}
}
signed main() {
scanf("%lld%lld", &n, &m); memset(h, -1, sizeof h);
for (int i = 1; i < n; ++i) {
int u, v, w, s, t; scanf("%lld%lld%lld%lld%lld", &u, &v, &w, &s, &t);
add(u, v, w, s, t), add(v, u, w, s, t);
}
l[0] = 0, r[0] = (int)1e18;
dfs(0, 0, 0);
while (m -- ) {
int c, t; scanf("%lld%lld", &t, &c);
if ((l[t] <= c && c <= r[t]) || !t) puts("YES");
else puts("NO");
}
return 0;
}
U312894 工资:dfs,线段树(绿)
dfs 处理出 dfn 序,用一棵线段树维护区间修改,单点查询。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <vector>
using namespace std;
#define int long long
const int N = 5e5+10;
int n, m, a[N], w[N];
int idx, dfn[N], size[N];
vector<int> e[N];
void dfs(int u) {
dfn[u] = ++ idx, w[idx] = a[u], size[u] = 1;
for (auto v : e[u]) dfs(v), size[u] += size[v];
}
struct Node {
int l, r, sum, add;
} seg[N<<2];
void Pushdown(Node &u, Node &fa) {
u.sum += (u.r - u.l + 1) * fa.add, u.add += fa.add;
}
void pushdown(int u) {
if (seg[u].add) {
Pushdown(seg[u<<1], seg[u]), Pushdown(seg[u<<1|1], seg[u]);
seg[u].add = 0;
}
}
void build(int u, int l, int r) {
seg[u].l = l, seg[u].r = r;
if (l == r) {seg[u].sum = w[l]; return ;}
int mid = l + r >> 1;
build(u<<1, l, mid), build(u<<1|1, mid+1, r);
}
int query(int u, int pos) {
if (seg[u].l == pos && seg[u].r == pos) return seg[u].sum;
pushdown(u);
int mid = seg[u].l + seg[u].r >> 1;
if (pos <= mid) return query(u<<1, pos);
else return query(u<<1|1, pos);
}
void modify(int u, int l, int r, int v) {
if (seg[u].l >= l && seg[u].r <= r) {Node t; t.add = v, Pushdown(seg[u], t); return ;}
pushdown(u);
int mid = seg[u].l + seg[u].r >> 1;
if (l <= mid) modify(u<<1, l, r, v);
if (r > mid) modify(u<<1|1, l, r, v);
}
signed main() {
cin >> n >> m >> a[1];
for (int i = 2; i <= n; ++i) {
int f; cin >> a[i] >> f;
e[f].push_back(i);
}
dfs(1), build(1, 1, n);
char op; int pos, x;
while (m -- ) {
cin >> op >> pos;
if (op == 'p') {cin >> x; modify(1, dfn[pos], dfn[pos]+size[pos]-1, x), modify(1, dfn[pos], dfn[pos], -x);}
else cout << query(1, dfn[pos]) << '\n';
}
return 0;
}
U312895 坤坤数:数位 dp(蓝)
\(f_{i,j,0/1}\) 表示从低到高 \(i\) 位,模 \(k\) 的值为 \(j\),有/无前导 \(0\) 的情况数量。有几个边界情况:
-
\(j=0\)(当前数模 \(k\) 为 \(0\))且无前导 \(0\):
-
\(i=n\):此时已经遍历到最高位,只有 \(1\) 种情况;
-
\(i\ne n\):则最高位一定为 \(1\sim 9\),第 \(2\sim n-d\) 位可以填 \(0\sim 9\),有 \(9\times 10^{n-d-1}\) 种情况。
-
-
\(i=n\) 且 \(j\ne 0\) 或有前导 \(0\):不可能存在这种情况,答案为 \(0\)。
采用 dfs 的做法,状态转移方程为:
注意我们需要预处理 \(10\) 的幂次。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
#define int long long
const int N = 1010, M = 110;
int n, m, k, powk[N], powm[N];
int f[N][M][2];
int dfs(int digit, int mod, bool zero) {
if (f[digit][mod][zero] >= 0) return f[digit][mod][zero];
if (!mod && zero) {
if (digit == n) return f[digit][mod][zero] = 1;
else return f[digit][mod][zero] = powm[n-digit-1] * 9 % m;
} if (digit == n) return f[digit][mod][zero] = 0;
f[digit][mod][zero] = 0;
for (int i = 0; i <= 9; ++i)
f[digit][mod][zero] = (f[digit][mod][zero] + dfs(digit+1, (mod+powk[digit]*i)%k, zero||i)) % m;
return f[digit][mod][zero];
}
signed main() {
scanf("%lld%lld%lld", &n, &k, &m);
memset(f, -1, sizeof f);
powk[0] = powm[0] = 1;
for (int i = 1; i <= 1000; ++i) powk[i] = powk[i-1]*10 % k, powm[i] = powm[i-1]*10 % m;
printf("%lld\n", dfs(0, 0, 0));
return 0;
}
P3855 [TJOI2008] Binary Land:bfs(绿)
暴力搜索即可。注意实现。
点击查看代码
#include <iostream>
#include <queue>
using namespace std;
const int N = 35, dx[] = {1, -1, 0, 0}, dy[] = {0, 0, -1, 1};
struct State {
int x1, y1, x2, y2, cnt;
};
int r, c;
int x1, y1, x2, y2, xs, ys;
bool st[N][N][N][N];
char map[N][N];
int bfs() {
queue<State> q; q.push({x1, y1, x2, y2, 0});
while (q.size()) {
if (q.size() > 100000) return -1;
auto t = q.front(); q.pop();
int x1 = t.x1, y1 = t.y1, x2 = t.x2, y2 = t.y2, cnt = t.cnt;
if (x1 == xs && y1 == ys && x2 == xs && y2 == ys) return cnt;
st[x1][y1][x2][y2] = 1;
for (int i = 0; i < 4; ++i) {
int x1_ = x1+dx[i], y1_ = y1+dy[i], x2_ = x2+dx[i], y2_ = y2+(-dy[i]);
if (x1_ < 1 || y1_ < 1 || x2_ < 1 || y2_ < 1 || x1_ > r || y1_ > c || x2_ > r || y2_ > c)
continue;
if (map[x1_][y1_] == '#') x1_ = x1, y1_ = y1;
else if (map[x1_][y1_] == 'X') continue;
if (map[x2_][y2_] == '#') x2_ = x2, y2_ = y2;
else if (map[x2_][y2_] == 'X') continue;
if (!st[x1_][y1_][x2_][y2_]) q.push({x1_, y1_, x2_, y2_, cnt+1}), st[x1_][y1_][x2_][y2_] = 1;
}
}
return -1;
}
int main() {
cin >> r >> c;
for (int i = 1; i <= r; ++i) {
for (int j = 1; j <= c; ++j) {
cin >> map[i][j];
if (map[i][j] == 'M') x1 = i, y1 = j;
else if (map[i][j] == 'G') x2 = i, y2 = j;
else if (map[i][j] == 'T') xs = i, ys = j;
}
}
int ans = bfs();
if (ans == -1) cout << "no" << '\n';
else cout << ans << '\n';
return 0;
}
7.16(Day 7)
P3195 [HNOI2008] 玩具装箱:斜率优化 dp(紫)
显然地,令 \(f_i\) 表示前 \(i\) 个玩具所需的总费用,\(s_i=\sum_{j=1}^i c_j\),则状态转移方程为:
用一点数学技巧,假设能从 \(f_j\) 转移至 \(f_i\),可以得到:
则 \(y=2(L+1)(j+s_j)+(j+s_j)^2+f_j\),\(x=(j+s_j)\),\(k=2(i+sum_i)\),单调性显然。
维护一个下凸壳的右半部分即可。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <deque>
using namespace std;
#define int long long
const int N = 5e4+10;
int n, l, s[N], f[N];
deque<int> q;
int get_x(int j) {
return j+s[j];
}
int get_y(int j) {
return 2*(l+1)*(j+s[j]) + (j+s[j])*(j+s[j]) + f[j];
}
signed main() {
scanf("%lld%lld", &n, &l);
for (int i = 1; i <= n; ++i) scanf("%lld", &s[i]), s[i] += s[i-1];
q.push_back(0);
for (int i = 1; i <= n; ++i) {
int k = 2*(i+s[i]);
while (q.size() > 1 &&
(get_y(q[1])-get_y(q[0])) <= k*(get_x(q[1])-get_x(q[0])))
q.pop_front();
int j = q[0]; f[i] = f[j] + (int)pow(i-j-1+s[i]-s[j]-l, 2);
int t = q.size() - 1;
while (q.size() > 1 &&
(get_y(q[t])-get_y(q[t-1]))*(get_x(i)-get_x(q[t])) >= ((get_y(i)-get_y(q[t]))*(get_x(q[t])-get_x(q[t-1]))))
q.pop_back(), t --;
q.push_back(i);
}
printf("%lld\n", f[n]);
return 0;
}
P5785 [SDOI2012] 任务安排:二分斜率优化 dp(紫)
先拿出 \(f_j\) 转移到 \(f_i\) 的式子:
令 \(y=f_j,x+sumC_j,k_i=S+sumT_i\),我们需要让截距最小。
那么我们维护一个下凸壳,单调队列维护斜率单调递增,每次二分查找第一个 \(k_{j-1,j}\le k_i<k_{j,j+1}\)。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <deque>
using namespace std;
#define int long long
const int N = 3e5+10;
int n, s, t[N], c[N], f[N];
deque<int> q;
int find(int num) {
int l = 0, r = q.size()-1;
while (l < r) {
int mid = l + r + 1 >> 1;
if ((f[q[mid]]-f[q[mid-1]]) <= num*(c[q[mid]]-c[q[mid-1]])) l = mid;
else r = mid-1;
}
return l;
}
signed main() {
scanf("%lld%lld", &n, &s);
for (int i = 1; i <= n; ++i) scanf("%lld%lld", &t[i], &c[i]), t[i] += t[i-1], c[i] += c[i-1];
q.push_back(0);
for (int i = 1; i <= n; ++i) {
int j = (q.size() > 1) ? (q[find(s+t[i])]) : 0;
f[i] = f[j] + s*(c[n]-c[j]) + t[i]*(c[i]-c[j]);
int r = q.size()-1;
while (q.size() > 1 &&
(f[i]-f[q[r]])*(c[q[r]]-c[q[r-1]]) <= (f[q[r]]-f[q[r-1]])*(c[i]-c[q[r]]))
q.pop_back(), r --;
q.push_back(i);
}
printf("%lld\n", f[n]);
return 0;
}
Day 7 模拟赛:
U312901 疯狂核电站:dp,矩阵快速幂,分治(紫)
令 \(f_i\) 表示前 \(i\) 个数中的合法序列数量。初始状态为 \(\forall 0\le i\le C,f_i=2^i\),\(f_{C+1}=2^{C+1}-1\)。我们可以在第 \(i\) 位前放 \(j\;(0\le j\le C)\) 个 \(1\),并再在它们前面放一个 \(0\)。则状态转移方程为:
注意到 \(f_{i-1}=\sum_{j=1}^C f_{i-j-1}\),则 \(f_{i}=2f_{i-1}-f_{i-C-1}\)。时间复杂度 \(O(n)\),可以通过后 \(20\%\) 的数据。
这个递推式显然可以用矩阵快速幂优化:
时间复杂度 \(O(C^3\log n)\),可以通过前 \(80\%\) 的数据。但由于矩阵乘法常数巨大,需要一些常数优化(循环展开,减少取模)。
把这两个做法合到一起就可以通过本题。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
typedef long long ll;
const int N = 1e6+10, M = 1010, P = 1e9+7;
ll n; int c, f[N];
void solve1() {
f[0] = 1;
for (int i = 1; i <= n; ++i) {
if (i <= c) f[i] = f[i-1] * 2 % P;
else if (i == c+1) f[i] = (((ll)f[i-1] * 2 - 1) % P + P) % P;
else f[i] = (((ll)2*f[i-1] - f[i-c-2]) % P + P) % P;
}
printf("%lld\n", f[n]);
}
struct Matrix {
int a[M][M];
Matrix () {
memset(a, 0, sizeof a);
}
};
Matrix operator*(const Matrix &x, const Matrix &y) {
Matrix ans;
for (int k = 0; k <= c+1; ++k) {
for (int i = 0; i <= c+1; ++i)
for (int j = 0; j <= c+1; ++j)
ans.a[i][j] = (ans.a[i][j] + (ll)x.a[i][k]*y.a[k][j]) % P;
}
return ans;
}
Matrix power(Matrix &a, ll b) {
if (b < 0) return a;
Matrix res;
for (int i = 0; i <= c+1; i += 8) res.a[i][i] = res.a[i+1][i+1] = res.a[i+2][i+2] = res.a[i+3][i+3] = res.a[i+4][i+4] = res.a[i+5][i+5] = res.a[i+6][i+6] = res.a[i+7][i+7] = 1;
while (b) {
if (b & 1) res = res * a;
a = a * a;
b >>= 1;
}
return res;
}
void solve2() {
Matrix a, trans;
a.a[0][0] = 1;
for (int i = 1; i <= c; i += 3) {
a.a[0][i] = 2ll * a.a[0][i-1]; if (a.a[0][i] > P) a.a[0][i] -= P;
a.a[0][i+1] = 2ll * a.a[0][i] % P; if (a.a[0][i+1] > P) a.a[0][i+1] -= P;
a.a[0][i+2] = 2ll * a.a[0][i+1] % P; if (a.a[0][i+2] > P) a.a[0][i+2] -= P;
}
a.a[0][c+1] = ((2ll*a.a[0][c]-1) % P + P) % P;
for (int i = 1; i <= c+1; i += 8) trans.a[i][i-1] = trans.a[i+1][i] = trans.a[i+2][i+1] = trans.a[i+3][i+2] = trans.a[i+4][i+3] = trans.a[i+5][i+4] = trans.a[i+6][i+5] = trans.a[i+7][i+6] = 1;
trans.a[0][c+1] = P-1, trans.a[c+1][c+1] = 2;
if (n <= c+1) printf("%d\n", a.a[0][n]);
else {
Matrix t = power(trans, n-c-1);
a = a * t;
printf("%d\n", a.a[0][c+1]);
}
}
signed main() {
scanf("%lld%d", &n, &c);
if (n < N) solve1();
else solve2();
return 0;
}
U312902 乖乖和咪咪的游戏2:博弈论(蓝)
先考虑递推的做法。令 \(f_i\) 表示 \(i\) 第一次最少要拿多少个圈才能必胜,初始状态为 \(f_1=1\)。状态转移时,从小到大枚举 \(j\),若 \(2j<f_{i-j}\),则后手一定不能取到只剩 \(i-j\) 个石子时的最小必胜圈数,\(f_i=j\)。
打个小表可以发现,只需要一直将 \(i\) 减去比 \(i\) 小的第一个斐波那契数,最后一个减去的即为答案。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
#define int long long
const int N = 210;
int i, n, f[N];
signed main() {
scanf("%lld", &n);
f[0] = f[1] = 1;
for (i = 2; f[i-1] <= n; ++i) f[i] = f[i-1] + f[i-2];
i --;
while (n > 0) {
if (n-f[i] == 0) printf("%lld\n", f[i]);
while (n >= f[i]) n -= f[i]; i --;
}
return 0;
}
U312903 鲁滨逊漂流记:LCA,树的直径(绿)
维护直径的两个端点 \(u,v\),对于每次新增的点判断其能否成为直径端点。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <vector>
using namespace std;
const int N = 2e5+10;
int u, v, ans;
int n; vector<int> e[N];
int idx, dep[N], dfn[N<<1], pos[N], st[N<<1][25];
void dfs(int u, int fa) {
dfn[++ idx] = u, pos[u] = idx;
for (auto v : e[u]) {
if (v == fa) continue;
dep[v] = dep[u] + 1, dfs(v, u), dfn[++ idx] = u;
}
}
int Min(int a, int b) {
return (pos[a] < pos[b]) ? a : b;
}
void init() {
for (int i = 1; i <= idx; ++i) st[i][0] = dfn[i];
for (int j = 1; (1<<j) <= idx; ++j) {
for (int i = 1; i+(1<<j)-1 <= idx; ++i)
st[i][j] = Min(st[i][j-1], st[i+(1<<j-1)][j-1]);
}
}
int query(int l, int r) {
if (l > r) swap(l, r);
int k = log2(r-l+1);
return Min(st[l][k], st[r-(1<<k)+1][k]);
}
int lca(int u, int v) {
return query(pos[u], pos[v]);
}
int main() {
scanf("%d", &n);
for (int i = 2; i <= n; ++i) {
int fa; scanf("%d", &fa);
e[fa].push_back(i);
}
dfs(1, 1), init();
u = 1, v = 1;
for (int i = 2; i <= n; ++i) {
int len1 = dep[u]+dep[i]-2*dep[lca(u, i)], len2 = dep[v]+dep[i]-2*dep[lca(v, i)];
if (len1 > ans) ans = len1, v = i;
if (len2 > ans) ans = len2, u = i;
printf("%d\n", ans);
}
return 0;
}
P7074 [CSP-J2020] 方格取数:前缀和,dp(黄)
令 \(f_{i,j}\) 表示走到点 \((i,j)\) 时获得的最大价值。由于可以往上下走,但只能往右走而不能往左走,所以我们需要先枚举列再枚举行。那么 \(f_{i,j}\) 可以从左边,上面和下面三个方向转移而来:
这样的时间复杂度是 \(O(n^3)\) 的,我们需要预处理出 \(s_i=\displaystyle\sum_{1\le t\le i} a_{i,j},pre_i=\max_{1\le t\le i}\{f_{t,j-1}-s_{t-1}\},suf_i=\max_{i\le t\le n}(f_{t,j-1}+s_t)\)。那么有:
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
#define int long long
const int N = 1010;
int n, m, a[N][N];
int pre[N], suf[N], s[N], f[N][N];
signed main() {
memset(f, -0x7f, sizeof f);
scanf("%lld%lld", &n, &m);
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= m; ++j)
scanf("%lld", &a[i][j]);
}
f[0][1] = 0;
for (int i = 1; i <= n; ++i) f[i][1] = f[i-1][1] + a[i][1];
for (int i = 2; i <= m; ++i) {
pre[0] = suf[n+1] = -(int)1e16;
for (int j = 1; j <= n; ++j) pre[j] = max(pre[j-1], f[j][i-1]-s[j-1]), s[j] = s[j-1]+a[j][i];
for (int j = n; j >= 1; --j) suf[j] = max(suf[j+1], f[j][i-1]+s[j]);
for (int j = 1; j <= n; ++j) f[j][i] = max(a[j][i]+f[j][i-1], max(pre[j]+s[j], suf[j]-s[j-1]));
}
printf("%lld\n", f[n][m]);
return 0;
}
7.17(Day 8)
CF1848A. Vika and Her Friends:数学(橙)
如果一个朋友 \(i\) 满足 \((|x_i-x|+|y_i-y|)\equiv 0\pmod 2\),则她一定可以把 Vike 逼到角上并抓住她。否则,她一定会与 Vika 擦肩而过。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
int t, n, m, k, x, y;
int main() {
scanf("%d", &t);
while (t -- ) {
scanf("%d%d%d%d%d", &n, &m, &k, &x, &y);
int xt, yt;
bool check = 0;
for (int i = 1; i <= k; ++i) {
scanf("%d%d", &xt, &yt);
if ((abs(xt-x)+abs(yt-y)) % 2 == 0) check = 1;
}
if (check) puts("NO");
else puts("YES");
}
return 0;
}
CF1848B. Vika and the Bridge:枚举(黄)
枚举每种颜色跳跃的最大距离 \(max\) 和次大距离 \(max'\),若增加一块颜色为 \(i\) 的木板,则该种颜色的最大距离变为 \(\max\left\{\left\lfloor \dfrac{max}{2} \right\rfloor,max'\right\}\)。取最小值即可。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 2e5+10;
int t, n, k, ans, c[N];
int last[N], Max[N][2];
int main() {
scanf("%d", &t);
while (t -- ) {
scanf("%d%d", &n, &k); ans = (int)1e9;
for (int i = 1; i <= k; ++i) last[i] = 0, Max[i][0] = Max[i][1] = -1;
for (int i = 1; i <= n; ++i) {
scanf("%d", &c[i]);
if (i-last[c[i]]-1 >= Max[c[i]][0]) Max[c[i]][1] = Max[c[i]][0], Max[c[i]][0] = i-last[c[i]]-1;
else if (i-last[c[i]]-1 > Max[c[i]][1]) Max[c[i]][1] = i-last[c[i]]-1;
last[c[i]] = i;
}
for (int i = 1; i <= k; ++i) {
if (n-last[i] >= Max[i][0]) Max[i][1] = Max[i][0], Max[i][0] = n-last[i];
else if (n-last[i] > Max[i][1]) Max[i][1] = n-last[i];
if (Max[i][0] == -1) continue;
ans = min(ans, max(Max[i][0]/2, Max[i][1]));
}
printf("%d\n", ans);
}
return 0;
}
CF1848C. Vika and Price Tags:数学,gcd(绿)
显然 \(x,y\) 经过一系列辗转相减后一定会变成 \(0\),最后进入 \(d,d,0,d,d,0,\cdots\) 的循环,其中 \(d=\gcd(x,y)\)。所以我们只需要判断 \(a_i,b_i\) 辗转相减得到的操作序列模 \(3\) 的余数是否相同即可。那么我们可以将操作序列中的所有数都除以 \(d\),将奇数视为 \(0\),将偶数视为 \(1\),那么一定会变为 \(\cdots,1,1,0,1,1,0\) 的循环。
观察这个循环可以发现,若 \(x,y\) 在序列中为 \(1,1\),则操作序列长度模 \(3\) 余 \(0\);若 \(x,y\) 在序列中为 \(1,0\),则操作序列长度模 \(3\) 余 \(2\);若 \(x,y\) 在序列中为 \(0,1\),则操作序列长度模 \(3\) 余 \(1\)。注意特判 \(x=y=0\) 的情况。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 1e5+10;
int t, n, cnt = -1, a[N], b[N];
int main() {
scanf("%d", &t);
while (t -- ) {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
for (int i = 1; i <= n; ++i) scanf("%d", &b[i]);
bool check = 1; cnt = -1;
for (int i = 1; i <= n; ++i) {
int mod;
if (!a[i] && !b[i]) continue;
if (!a[i]) mod = 1;
if (!b[i]) mod = 2;
else {
int d = __gcd(a[i], b[i]), x = a[i]/d, y = b[i]/d;
if (x % 2) x = 1; else x = 0;
if (y % 2) y = 1; else y = 0;
if (!x && y) mod = 1; else if (x && y) mod = 0; else mod = 2;
}
if (cnt == -1) cnt = mod;
else if (cnt != mod) check = 0;
}
(check) ? puts("YES") : puts("NO");
}
return 0;
}
Day 8 模拟赛:
U312977 吉利的楼层:数位 dp(蓝)
和上面的 HDU2089. 不要62 方法一样。操作二可以二分解决。
注意要预处理 \(10\) 的幂次,优化常数。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
using namespace std;
#define int long long
int n, t, x, f[20][10], pow10[20];
void init() {
int sum = 0;
for (int i = 0; i <= 9; ++i) f[1][i] = (i == 4) ? 0 : 1, sum += f[1][i];
for (int i = 2; i <= 17; ++i) {
int tmp = 0;
for (int j = 0; j <= 9; ++j) {
if (j == 4) continue;
if (j == 1) f[i][j] = sum - f[i-1][3];
else f[i][j] = sum;
tmp += f[i][j];
}
sum = tmp;
}
}
int get(int x) {
int last = 0, ans = 0;
for (int i = ceil(log10(x)); i >= 1; --i) {
int num = x / (int)pow10[i-1];
for (int j = 0; j < num; ++j) {
if (j == 4) continue;
if (last == 1 && j == 3) continue;
ans += f[i][j];
}
if ((num == 4) || (last == 1 && num == 3)) break;
x -= num * pow10[i-1], last = num;
}
return ans;
}
bool check(int x) {
int last = 0;
while (x) {
int num = x % 10;
if (num == 4 || (last == 3 && num == 1)) return 0;
x /= 10, last = num;
}
return 1;
}
int find(int x) {
int l = 1, r = (int)1e17, cnt = 0;
while (l < r) {
int mid = l + r + 1 >> 1;
if (get(mid+1)-1 >= x) r = mid-1;
else l = mid;
}
return l+1;
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
init();
cin >> n;
pow10[0] = 1;
for (int i = 1; i <= 16; ++i) pow10[i] = pow10[i-1] * 10;
while (n -- ) {
cin >> t >> x;
if (t == 1) cout << ((check(x))?(get(x+1)-1):-1) << '\n';
else cout << find(x) << '\n';
}
return 0;
}
U312978 采蘑菇2(* 加强版 CF436E. Cardboard Box):(反悔)贪心(紫)
对于第 \(i\) 种蘑菇,我们有两种选择:花费 \(a_i\) 的代价得到一个蘑菇,花费 \(a_i+b_i\) 的代价得到两个蘑菇。
那么我们可以将 \(a_i\) 和 \(a_i+b_i\) 分别插入两个小根堆中。每次判断最小的 \(a_i+b_i\) 是否比最小的 \(a_j+a_k\) 更优,权衡选一个还是选两个。最后用一个 \(check\) 数组标记是否取过。
对于加强版,我们还需要为每次花费最小的位置上的星星数量增加 \(1\)。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <queue>
using namespace std;
#define int long long
typedef pair<int, int> pii;
const int N = 2e5+10;
int n, m, ans, a[N<<1], check[N<<1];
priority_queue<pii, vector<pii>, greater<pii>> q1, q2;
void clear(priority_queue<pii, vector<pii>, greater<pii>> &q) { // 找到有效的位置
while (!q.empty() && check[q.top().second]) q.pop();
}
signed main() {
scanf("%lld%lld", &n, &m);
for (int i = 1; i <= n; ++i)
scanf("%lld%lld", &a[i], &a[i+n]), q1.push({a[i], i}), q2.push({a[i]+a[i+n], i});
while (m -- ) {
clear(q1); int pos = q1.top().second; q1.pop();
clear(q1), clear(q2);
if (m && q2.size() && a[pos]+q1.top().first >= q2.top().first)
// 判断选1个还是选1组中的两个
q1.push({a[pos], pos}), pos = q2.top().second, q2.pop();
if (pos <= n) q1.push({a[pos+n], pos+n});
ans += a[pos], check[pos] = 1;
}
printf("%lld\n", ans);
return 0;
}
U312979 乖乖和元宝的游戏:博弈论(蓝)
打表(记忆化搜索)可以发现,若 \(a_i\) 中模 \(0,1,2\) 的个数分别为 \(x,y,z\),则在 \(y,z\) 均为 \(2\) 的倍数时元宝必胜。下面给出打表代码:
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 25;
int f[N][N][N][4];
bool check(int a, int b, int c) {
int cnt0 = 0, cnt1 = 0;
if (a == 0) cnt0 ++; else if (a == 1) cnt1 ++;
if (b == 0) cnt0 ++; else if (b == 1) cnt1 ++;
if (c == 0) cnt0 ++; else if (c == 1) cnt1 ++;
if (cnt1 && !cnt0) return 1;
return 0;
}
int dfs(int a, int b, int c, int sum) {
if (a < 0 || b < 0 || c < 0) return -1;
if (f[a][b][c][sum] != -1) return f[a][b][c][sum];
if (a+b+c == 1) {
if (a) return f[a][b][c][sum] = ((sum%3 == 0) ? 0 : 1);
if (b) return f[a][b][c][sum] = (((1+sum)%3 == 0) ? 0 : 1);
if (c) return f[a][b][c][sum] = (((2+sum)%3 == 0) ? 0 : 1);
}
if (!a && !b && !c) return f[a][b][c][sum] = ((sum == 0) ? 0 : 1);
f[a][b][c][sum] = check(dfs(a-2, b, c, sum), dfs(a-1, b-1, c, (sum+2)%3), dfs(a-1, b, c-1, (sum+1)%3)) |
check(dfs(a, b-2, c, sum), dfs(a-1, b-1, c, (sum+1)%3), dfs(a, b-1, c-1, (sum+2)%3)) |
check(dfs(a, b, c-2, sum), dfs(a-1, b, c-1, (sum+2)%3), dfs(a, b-1, c-1, (sum+1)%3));
return f[a][b][c][sum];
}
int main() {
freopen("C.ans", "w", stdout);
memset(f, -1, sizeof f);
for (int i = 0; i <= 5; ++i) {
for (int j = 0; j <= 10; ++j)
for (int k = 0; k <= 10; ++k) {
dfs(i, j, k, 0);
if (!f[i][j][k][0]) printf("%d %d %d\n", i, j, k);
}
}
return 0;
}
感性理解一下,\(0\) 对答案肯定没有影响,\(1\) 和 \(2\) 如果数量均为偶数,可以通过轮流取的方式来抵消。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
int n, a, b, c;
int main() {
scanf("%d", &n);
while (n -- ) {
int f = 1, sum = 0; string s; cin >> s;
if (s[0] == '-') f = -1;
for (int i = 0; i < s.size(); ++i) {
if (!isdigit(s[i])) continue;
sum += s[i]-'0';
}
sum %= 3; if (f == -1) sum = (3-sum) % 3;
if (!sum) a ++; else if (sum == 1) b ++; else c ++;
}
int cnt = 0;
if (b % 2 == 0 && c % 2 == 0) puts("Yuanbao");
else puts("Guai");
return 0;
}
7.18(Day 9)
P4072 [SDOI2016] 征途:斜率优化 dp(紫)
首先要推一下方差的式子:
后面一项是定值,所以只需要计算 \(\sum_{i=1}^m dis_i\) 的最小值即可。
令 \(f_{i,j}\) 表示考虑前 \(i\) 条路,\(j\) 天走完的最小 \(\sum dis^2\)。则状态转移方程为:
令 \(s_i\) 为 \(a\) 的前缀和。因为我不会写二维的斜率优化,所以先滚掉一维,变为:
假设能从 \(g_k\) 转移到 \(f_i\),则有:
画图可以发现我们需要维护一个下凸壳的右半部分。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <deque>
using namespace std;
typedef long long ll;
const int N = 3010;
int n, m, s[N]; ll f[N], g[N];
int getx(int i) {
return s[i];
}
int gety(int i) {
return s[i]*s[i] + g[i];
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++i) scanf("%d", &s[i]), s[i] += s[i-1], g[i] = s[i]*s[i];
for (int j = 2; j <= m; ++j) {
deque<int> q; q.push_back(0);
for (int i = 1; i <= n; ++i) {
int k = 2 * s[i];
while (q.size() > 1 &&
(gety(q[1])-gety(q[0])) <= k*(getx(q[1])-getx(q[0])))
q.pop_front();
int t = q[0]; f[i] = g[t] + s[t]*s[t] - 2*s[i]*s[t] + s[i]*s[i];
t = q.size() - 1;
while (q.size() > 1 &&
(gety(i)-gety(q[t]))*(getx(q[t])-getx(q[t-1])) <= (gety(q[t])-gety(q[t-1]))*(getx(i)-getx(q[t])))
q.pop_back(), t --;
q.push_back(i);
}
memcpy(g, f, sizeof g);
}
printf("%lld\n", m*f[n]-s[n]*s[n]);
return 0;
}
Day 9 模拟赛:
P2657 [SCOI2009] windy 数:数位 dp(蓝)
记忆化搜索即可。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
int a, b, k, num[15], f[12][12];
int dfs(int digit, int last, bool limit, bool zero) {
// digit: 当前位数, last: 上一位, limit: 当前这一位是否取到最大值, zero: 是否有前导0
if (!digit) return 1;
if (!limit && !zero && f[digit][last] != -1) return f[digit][last];
int res = 0;
int maxl = (limit) ? num[digit] : 9;
for (int i = 0; i <= maxl; ++i) {
if (abs(i-last) >= 2 || zero)
res += dfs(digit-1, i, limit&&(i==num[digit]), zero&&(i==0));
}
if (!limit && !zero) f[digit][last] = res;
return res;
}
int get(int x) {
k = 0;
while (x) {
num[++ k] = x % 10;
x /= 10;
}
memset(f, -1, sizeof f);
return dfs(k, -100, 1, 1);
}
int main() {
scanf("%d%d", &a, &b);
printf("%d\n", get(b)-get(a-1));
return 0;
}
U313891 异或派:01 Trie(黄)
01 Trie 板子题。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
#define int long long
const int N = 4e6+10;
int n, p, idx, son[N][2], a[N], ans;
void insert(int x) {
int u = 0;
for (int i = 35; i >= 0; --i) {
int t = (x>>i) & 1;
if (!son[u][t]) son[u][t] = ++ idx;
u = son[u][t];
}
}
int query(int x) {
int u = 0, ans = 0;
for (int i = 35; i >= 0; --i) {
int t = (x>>i) & 1;
if (!son[u][!t]) u = son[u][t];
else u = son[u][!t], ans += (1<<i);
}
return ans;
}
signed main() {
scanf("%lld%lld", &n, &p);
for (int i = 1; i <= n; ++i) scanf("%lld", &a[i]), insert(a[i]);
for (int i = 1; i <= n; ++i) ans = max(ans, query(a[i]));
printf("%lld\n", ans*(p-1));
return 0;
}
U313893 彩虹桥:Floyd(绿)
倒序处理最短路。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <vector>
using namespace std;
typedef pair<int, int> pii;
const int N = 510, M = 5e5+10, inf = 1e9;
int n, m, s, b, d;
int f[N][N];
bool check[N];
int pre[M];
struct Oper {
int op, x, ans;
} oper[M];
void floyd() {
for (int k = 1; k <= n; ++k) {
if (!check[k])
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= n; ++j)
f[i][j] = min(f[i][j], f[i][k]+f[k][j]);
}
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m >> s >> d >> b;
for (int i = 1; i <= n; ++i) {
for (int j = i+1; j <= n; ++j)
f[i][j] = f[j][i] = inf;
}
for (int i = 1; i <= m; ++i) {
int u, v, w; cin >> u >> v >> w;
f[u][v] = f[v][u] = min(f[u][v], w);
}
for (int i = 1; i <= b+d; ++i) {
char op; int x; cin >> op >> x;
if (op == 'b') oper[i].op = 0, pre[i] = s, s = x;
else oper[i].op = 1, check[x] = 1;
oper[i].x = x, oper[i].ans = -2;
}
floyd();
for (int i = b+d; i >= 1; --i) {
if (oper[i].op) {
for (int j = 1; j <= n; ++j) {
for (int k = 1; k <= n; ++k)
f[j][k] = min(f[j][k], f[j][oper[i].x]+f[oper[i].x][k]);
}
} else oper[i].ans = (f[oper[i].x][pre[i]] == inf) ? -1 : f[oper[i].x][pre[i]];
}
for (int i = 1; i <= b+d; ++i) if (oper[i].ans >= -1) cout << oper[i].ans << '\n';
return 0;
}
CF559C. Gerald and Giant Chess:数学(蓝)(加强版:AT_dp_y. Grid 2.cpp)
先考虑没有陷阱的情况,则答案为 \(\displaystyle\binom{n+m-2}{n-1}\)。
由于陷阱之间的答案会相互影响,我们需要将所有陷阱以 \(x\) 为第一关键字,\(y\) 为第二关键字排序。对于两个陷阱 \((x_1,y_1)\) 和 \((x_2,y_2)\) ,若满足 \(x_1\le x_2,y_1\le y_2\),则陷阱 \((x_1,y_1)\) 会影响 \((x_2,y_2)\),需要减去相应的值。
时间复杂度 \(O(n^2)\)。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
const int N = 2010, M = 3e5+10, P = 1e9+7;
int n, m, k; pii pos[N];
int sum, ans, tot[M];
int fac[M], infac[M];
int power(int a, int b) {
int ans = 1;
while (b) {
if (b & 1) ans = (ll)ans * a % P;
a = (ll)a * a % P;
b >>= 1;
}
return ans;
}
int calC(int b, int a) {
return (ll)fac[a] * infac[b] % P * infac[a-b] % P;
}
int main() {
fac[0] = 1, infac[0] = 1;
for (int i = 1; i <= 200000; ++i) fac[i] = (ll)fac[i-1] * i % P, infac[i] = power(fac[i], P-2);
scanf("%d%d%d", &n, &m, &k);
for (int i = 1; i <= k; ++i) scanf("%d%d", &pos[i].first, &pos[i].second);
sort(pos+1, pos+k+1);
ans = calC(n-1, n+m-2);
for (int i = 1; i <= k; ++i) {
int x = pos[i].first, y = pos[i].second;
int t = calC(x-1, x+y-2); t -= tot[i];
sum = (sum + (ll)t*calC(n-x, n+m-x-y)) % P;
for (int j = i+1; j <= k; ++j) {
if (x <= pos[j].first && y <= pos[j].second)
tot[j] = (tot[j] + (ll)t*calC(pos[j].first-x, pos[j].first+pos[j].second-x-y)) % P;
}
}
printf("%d\n", ((ans-sum)%P+P) % P);
return 0;
}
7.19(Day 10)
P4139 上帝与集合的正确用法:数学,扩展欧拉定理(紫)
由于 \(2^{2^{2^{\cdots}}}\) 有无穷多层,所以我们可以将每一次取模后的指数都视作相同的。
线性筛预处理 \(\varphi(p)\) 即可。
本题时间复杂度为 \(O(\log p)\)。证明:
- 若 \(p\bmod 2=0\):由于
\[ \varphi(p)=p\times\prod_{i=1}^m\left(1-\dfrac{1}{p_i}\right) \]一定有 \(\varphi(p)\le \dfrac{1}{2}p\)。
- 若 \(p\bmod 1=0\):则在上式中的分母至少有一项为偶数,\(\varphi(p)\bmod 2=0\)。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long ll;
const int N = 1e7+10;
int t, p;
int cnt, prime[N], phi[N];
bool st[N];
void Euler(int n) {
st[0] = st[1] = 1, phi[0] = phi[1] = 1;
for (int i = 2; i <= n; ++i) {
if (!st[i]) prime[++ cnt] = i, phi[i] = i-1;
for (int j = 1; prime[j] <= n/i && j <= cnt; ++j) {
st[i*prime[j]] = 1;
if (i % prime[j] == 0) {
phi[i*prime[j]] = phi[i] * prime[j];
break;
}
phi[i*prime[j]] = phi[i] * (prime[j]-1);
}
}
}
int power(int a, int b, int p) {
int res = 1;
while (b) {
if (b & 1) res = (ll)res * a % p;
a = (ll)a * a % p;
b >>= 1;
}
return res;
}
int solve(int p) {
if (p == 1) return 0;
return power(2, solve(phi[p])+phi[p], p);
}
int main() {
Euler((int)1e7);
scanf("%d", &t);
while (t -- ) {
scanf("%d", &p);
printf("%d\n", solve(p));
}
return 0;
}
P3934 [Ynoi2016] 炸脖龙 I:奈芙莲树(树状数组,扩展欧拉定理)(紫)
令 \(f_{l,r}=a_l^{a_{l+1}^{\cdots^{a_r}}}\),根据扩展欧拉定理,可以递归计算它的值。注意扩展欧拉定理需要分类讨论。
需要维护区间修改,单点查值,使用树状数组即可。
点击查看代码
#include <iostream>
#include <algorithm>
#include <cstdio>
using namespace std;
#define int long long
const int N = 5e5+10, M = 2e7+10;
int n, m, c[N];
int cnt, prime[M], phi[M]; bool st[M];
void Euler(int n) {
st[0] = st[1] = 1, phi[0] = phi[1] = 1;
for (int i = 2; i <= n; ++i) {
if (!st[i]) prime[++ cnt] = i, phi[i] = i-1;
for (int j = 1; prime[j] <= n/i && j <= cnt; ++j) {
st[i*prime[j]] = 1;
if (i % prime[j] == 0) {
phi[i*prime[j]] = phi[i] * prime[j];
break;
}
phi[i*prime[j]] = phi[i] * (prime[j]-1);
}
}
}
int lowbit(int x) {
return x & -x;
}
void add(int pos, int x) {
for (int i = pos; i <= n; i += lowbit(i))
c[i] += x;
}
int query(int pos) {
int sum = 0;
for (int i = pos; i >= 1; i -= lowbit(i))
sum += c[i];
return sum;
}
struct Node {
int v; bool flag; // v存储值, flag存储是否>=p
Node (int v = 0, bool flag = false) : v(v), flag(flag) {}
};
Node power(int a, int b, int p) { // 在快速幂的过程中判断是否>=p
Node res = Node(1, 0);
if (a >= p) a %= p, res.flag = 1;
while (b) {
if (b & 1) res.v *= a;
if (res.v >= p) res.flag = 1, res.v %= p;
a *= a;
if (a >= p) res.flag = 1, a %= p;
b >>= 1;
}
return res;
}
Node solve(int l, int r, int p) {
int L = query(l);
if (p == 1) return Node(0, 1);
if (L == 1) return Node(1, 0);
if (l == r) return (L<p) ? Node(L, 0) : Node(L%p, 1);
Node res = solve(l+1, r, phi[p]);
if (res.flag) res.v += phi[p]; // 如果>=p,根据扩展欧拉定理指数还需要加上phi[p]
return power(L, res.v, p);
}
signed main() {
Euler((int)2e7);
scanf("%lld%lld", &n, &m);
for (int i = 1; i <= n; ++i) {
int x; scanf("%lld", &x);
add(i, x), add(i+1, -x);
}
int op, l, r, x;
while (m -- ) {
scanf("%lld%lld%lld%lld", &op, &l, &r, &x);
if (op == 1) add(l, x), add(r+1, -x);
else printf("%lld\n", solve(l, r, x).v);
}
return 0;
}
Day 10 模拟赛:
P5149 会议座位:树状数组,逆序对(绿)
map 存一下每个名字对应的编号,然后就变成树状数组求逆序对的板子。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <unordered_map>
using namespace std;
typedef long long ll;
const int N = 1e5+10;
int n, idx, c[N]; ll ans;
unordered_map<string, int> name;
string ss[N];
int lowbit(int x) {
return x & -x;
}
void add(int pos, int x) {
for (int i = pos; i <= idx; i += lowbit(i))
c[i] += x;
}
int query(int pos) {
int sum = 0;
for (int i = pos; i >= 1; i -= lowbit(i))
sum += c[i];
return sum;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n;
for (int i = 1; i <= n; ++i) {
string s; cin >> s;
name[s] = ++ idx;
}
for (int i = 1; i <= n; ++i) cin >> ss[i];
for (int i = n; i >= 1; --i) {
int now = name[ss[i]];
ans += query(now); add(now, 1);
}
cout << ans << '\n';
return 0;
}
CF1195E. OpenStreetMap:RMQ,单调队列(蓝)
令 \(f_{i,j,k}\) 表示以 \((i,j)\) 为开头,向右 \(2^k\) 个数中的最小值,预处理方式同普通 ST 表。枚举矩形左上角顶点,单调队列维护矩形内最小值。
由于本题非常卡空间,且 RMQ 查询的区间长度相同,需要采用滚动数组优化。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <deque>
#include <cmath>
using namespace std;
const int N = 3002;
typedef long long ll;
typedef pair<int, int> pii;
int n, m, a, b, x, y, z, last, f[N][N][2];
ll ans;
int query(int x, int l, int r) {
int k = log2(r-l+1);
return min(f[x][l][k&1], f[x][r-(1<<k)+1][k&1]);
}
int main() {
scanf("%d%d%d%d%d%d%d%d", &n, &m, &a, &b, &last, &x, &y, &z);
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= m; ++j)
f[i][j][0] = last, last = ((ll)x*last + y) % z;
}
for (int k = 1; 1<<k <= b; ++k) {
for (int i = 1; i <= n; ++i) {
for (int j = 1; j+(1<<k)-1 <= m; ++j)
f[i][j][k&1] = min(f[i][j][(k&1)^1], f[i][j+(1<<k-1)][(k&1)^1]);
}
}
deque<int> q;
for (int j = 1; j <= m-b+1; ++j) {
while (q.size()) q.pop_front();
for (int i = 1; i < a; ++i) {
int t = query(i, j, j+b-1), r = q.size()-1;
while (q.size() && query(q[r], j, j+b-1) >= t) q.pop_back(), r --;
q.push_back(i);
}
for (int i = a; i <= n; ++i) {
int t = query(i, j, j+b-1);
while (q.size() && q[0] < i-a+1) q.pop_front();
int r = q.size()-1;
while (q.size() && query(q[r], j, j+b-1) >= t) q.pop_back(), r --;
q.push_back(i);
ans += query(q[0], j, j+b-1);
}
}
printf("%lld\n", ans);
return 0;
}
7.20
P2073 送花:平衡树(set)(蓝)
fhq-treap 实现。删除最小值和最大值可以先找到排名为 \(1\) 和 \(size_{root}\) 的数,再将其对应的值删除。最后用 dfs 计算答案。细节还是挺多的。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long ll;
const int N = 1e5+10;
int root, idx;
ll beauty, cost;
struct Node {
int l, r;
int w, c, key; // 平衡树里存储w,c,但分裂时只看c的值
int size;
} tree[N];
void pushup(int u) {
tree[u].size = tree[tree[u].l].size + tree[tree[u].r].size + 1;
}
int newNode(int w, int c) {
++ idx;
tree[idx].l = tree[idx].r = 0;
tree[idx].w = w, tree[idx].c = c, tree[idx].key = rand();
tree[idx].size = 1;
return idx;
}
void split(int p, int c, int &x, int &y) {
if (!p) {x = y = 0; return ;}
if (tree[p].c <= c) x = p, split(tree[p].r, c, tree[p].r, y);
else y = p, split(tree[p].l, c, x, tree[p].l);
pushup(p);
}
int merge(int x, int y) {
if (!x || !y) return x+y;
if (tree[x].key <= tree[y].key) {
tree[x].r = merge(tree[x].r, y);
pushup(x); return x;
} else {
tree[y].l = merge(x, tree[y].l);
pushup(y); return y;
}
}
void insert(int w, int c) {
int x, y, z;
split(root, c, x, z), split(x, c-1, x, y);
if (tree[y].size) {root = merge(merge(x, y), z); return ;} // 不能插入也要拼起来
y = newNode(w, c);
root = merge(merge(x, y), z);
}
void del(int c) {
int x, y, z;
split(root, c, x, z), split(x, c-1, x, y);
y = merge(tree[y].l, tree[y].r);
root = merge(merge(x, y), z);
}
int get_num(int p, int k) {
if (tree[tree[p].l].size >= k) return get_num(tree[p].l, k);
else if (tree[tree[p].l].size+1 == k) return tree[p].c;
else return get_num(tree[p].r, k-tree[tree[p].l].size-1);
}
void get_ans(int p) {
if (!p) return ;
beauty += tree[p].w, cost += tree[p].c;
get_ans(tree[p].l), get_ans(tree[p].r);
}
int main() {
int op, w, c, t;
while (scanf("%d", &op)) {
if (op == -1) break;
if (op == 1) {
scanf("%d%d", &w, &c);
insert(w, c);
} else if (op == 2) {
if (!tree[root].size) continue; // 防止 RE
t = get_num(root, tree[root].size);
del(t);
} else {
if (!tree[root].size) continue;
t = get_num(root, 1);
del(t);
}
}
get_ans(root);
printf("%lld %lld\n", beauty, cost);
return 0;
}
P3478 [POI2008] STA-Station:换根 dp(绿)
令 \(f_i\) 表示以 \(i\) 为根节点,所有节点的深度之和。假设 \(i\) 为 \(j\) 的父亲节点,画图可以发现,当 \(j\) 替代 \(i\) 成为根节点时,以 \(j\) 为根的子树内所有节点的深度都减少了 \(1\)(包括 \(j\)),而其他节点的深度都增加了 \(1\)。所以状态转移方程为:
其中 \((i,j)\in E\)。
由于从 \(i\) 推到 \(j\) 的时间复杂度是 \(O(1)\) 的,而我们需要对整棵树进行遍历,时间复杂度 \(O(n)\)。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <vector>
using namespace std;
typedef long long ll;
const int N = 1e6+10;
using namespace std;
int n, size[N], dep[N]; ll ans, f[N];
vector<int> e[N];
void dfs(int u, int fa) {
size[u] = 1;
for (auto v : e[u]) {
if (v == fa) continue;
dep[v] = dep[u]+1, f[1] += dep[v];
dfs(v, u), size[u] += size[v];
}
return ;
}
void get_ans(int u, int fa) {
for (auto v : e[u]) {
if (v == fa) continue;
f[v] = f[u] - size[v] + (n-size[v]);
if (f[v] > f[ans]) ans = v;
get_ans(v, u);
}
return ;
}
int main() {
scanf("%d", &n);
for (int i = 1; i < n; ++i) {
int u, v; scanf("%d%d", &u, &v);
e[u].push_back(v), e[v].push_back(u);
}
dfs(1, 0);
ans = 1, get_ans(1, 0);
printf("%lld\n", ans);
return 0;
}
7.21
P2120 [ZJOI2007] 仓库建设:斜率优化 dp(紫)
令 \(f_i\) 表示考虑前 \(i\) 个工厂的最小花费,则状态转移方程为:
令 \(\displaystyle\sum_{1\le k\le i} p_k=sp_i,\sum_{1\le k\le i}p_kx_k=ss_i\),则有:
假设 \(f_i\) 能从 \(f_j\) 转移而来,变形可得:
斜率优化维护下凸壳右半部分即可。
注意最后连续的一段 \(p_i\sim p_n\) 可能为空,需要找到最后一个非空的工厂 \(last\),答案即为 \(\displaystyle\min_{last\le i\le n} f_i\)。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <deque>
using namespace std;
#define int long long
const int N = 1e6+10;
int n, last, ans = (int)1e18;
int x[N], sp[N], ss[N], c[N], f[N];
int gety(int j) {
return f[j] + ss[j];
}
signed main() {
scanf("%lld", &n);
for (int i = 1; i <= n; ++i) {
scanf("%lld%lld%lld", &x[i], &sp[i], &c[i]);
ss[i] = ss[i-1] + sp[i]*x[i], sp[i] += sp[i-1];
}
last = n; while (!(sp[last]-sp[last-1])) last --;
deque<int> q; q.push_front(0);
for (int i = 1; i <= n; ++i) {
int k = x[i];
while (q.size() > 1 &&
gety(q[1])-gety(q[0]) < k*(sp[q[1]]-sp[q[0]]))
q.pop_front();
int j = q[0];
f[i] = f[j] + x[i]*(sp[i]-sp[j]) - (ss[i]-ss[j]) + c[i];
int t = q.size() - 1;
while (q.size() > 1 &&
(gety(q[t])-gety(q[t-1]))*(sp[i]-sp[q[t]]) > (gety(i)-gety(q[t]))*(sp[q[t]]-sp[q[t-1]]))
q.pop_back(), t --;
q.push_back(i);
}
for (int i = last; i <= n; ++i) ans = min(ans, f[i]); printf("%lld\n", ans);
return 0;
}
P4136 谁能赢呢?:博弈论(绿)
显然最终整个棋盘都会被走完。那么当总格数为 \(2\) 的倍数时,先手必胜;反之后手必胜。由于 \(n^2\) 的奇偶性与 \(n\) 相同,直接判断 \(n\) 的奇偶性即可。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
int n;
int main() {
while (scanf("%d", &n)) {
if (!n) break;
(n % 2) ? puts("Bob") : puts("Alice");
}
return 0;
}
7.23
CF1853A. Desorting:枚举(橙)
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
using namespace std;
const int N = 510;
int t, n, a[N];
int main() {
scanf("%d", &t);
while (t -- ) {
int minl = 1e9;
scanf("%d", &n);
for (int i = 1; i <= n; ++i) {
scanf("%d", &a[i]);
if (i > 1) minl = min(minl, a[i]-a[i-1]);
}
if (minl < 0) puts("0");
else printf("%d\n", (int)ceil((minl+1)/2.0));
}
return 0;
}
CF1853B. Fibonaccharsis:数学,枚举(黄)
题目条件可以转化为求不定方程 \(n=f_kx+f_{k-1}y\) 的解,满足 \(y>x>0\)。枚举计算即可。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 2e5;
int t, n, k;
int idx, f[N];
int main() {
f[1] = 0, f[2] = 1;
for (idx = 3; f[idx-1] <= N; ++idx) f[idx] = f[idx-1] + f[idx-2];
scanf("%d", &t);
while (t -- ) {
scanf("%d%d", &n, &k);
if (k >= idx || n < f[k]) {puts("0"); continue;}
int a = f[k], b = f[k-1], ans = 0;
for (int i = 0; i <= n; ++i) {
int t = n - b * i;
if (i > t/a) break;
if (a != 0 && t % a == 0) ans ++; //printf("%d %d\n", i, t/a);
}
printf("%d\n", ans);
}
return 0;
}
CF1853C. Ntarsis' Set:二分(绿)
我们可以二分答案。对于当前的一个数 \(x\),每次找到当前能够删去的数的数量,判断能否重复 \(k\) 次。需要特判 \(a_1\ne 1\) 时答案为 \(1\)。
时间复杂度 \(O(k\log nk)\)。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long ll;
const int N = 2e5+10;
int t, n, k; ll a[N];
bool check(ll x) {
ll cnt = x, r = n;
for (int i = 1; i <= k; ++i) {
while (a[r] > cnt && r > 0) r --; // 由于cnt单调递减,可以用一个指针查找
if (r <= 0) return 0;
cnt -= r; // 删去能够删去的数
}
return (cnt > 0);
}
int main() {
scanf("%d", &t);
while (t -- ) {
scanf("%d%d", &n, &k);
for (int i = 1; i <= n; ++i) scanf("%lld", &a[i]);
if (a[1] != 1) {puts("1"); continue;}
ll l = 1, r = 4e10+1;
while (l < r) {
ll mid = l + r >> 1;
if (check(mid)) r = mid;
else l = mid+1;
}
printf("%lld\n", l);
}
return 0;
}
7.24
P1073 [NOIP2009 提高组] 最优贸易:BFS(绿)
令 \(minv_i\) 表示从起点到 \(i\) 点能够获得的最小价值,\(maxv_i\) 表示从 \(i\) 点到终点能够获得的最大价值。
我们需要记录从起点能够到达的点,将它们的值从小到大排序后更新它们能够到达的点的 \(minv_i\);建一个反图,记录从终点能够到达的点,将它们的值从大到小排序后更新它们能够到达的点的 \(maxv_i\)。
答案即为 \(\max_{1\le i\le n}\{maxv_i-min_i\}\)。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <queue>
using namespace std;
const int N = 1e5+10;
int n, m, ans, val[N];
int minv[N], maxv[N];
bool vis[N], fvis[N];
vector<int> e[N], fe[N];
bool cmp(int a, int b) {
return val[a] < val[b];
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++i) scanf("%d", &val[i]);
for (int i = 1; i <= m; ++i) {
int u, v, w; scanf("%d%d%d", &u, &v, &w);
e[u].push_back(v), fe[v].push_back(u);
if (w == 2) e[v].push_back(u), fe[u].push_back(v);
}
queue<int> q; vis[1] = 1, q.push(1);
vector<int> nums;
while (q.size()) {
int u = q.front(); q.pop();
nums.push_back(u);
for (auto v : e[u]) if (!vis[v]) vis[v] = 1, q.push(v);
}
sort(nums.begin(), nums.end(), cmp);
fvis[n] = 1, q.push(n);
vector<int> fnums;
while (q.size()) {
int u = q.front(); q.pop();
fnums.push_back(u);
for (auto v : fe[u]) if (!fvis[v]) fvis[v] = 1, q.push(v);
}
sort(fnums.begin(), fnums.end(), cmp);
memset(vis, 0, sizeof vis), memset(fvis, 0, sizeof fvis);
for (int i = 0; i < nums.size(); ++i) {
int u = nums[i];
if (vis[u]) continue;
vis[u] = 1, minv[u] = val[u], q.push(u);
while (q.size()) {
int t = q.front(); q.pop();
for (auto v : e[t]) if (!vis[v]) vis[v] = 1, minv[v] = val[u], q.push(v);
}
}
for (int i = fnums.size()-1; i >= 0; --i) {
int u = fnums[i];
if (fvis[u]) continue;
vis[u] = 1, maxv[u] = val[u], q.push(u);
while (q.size()) {
int t = q.front(); q.pop();
for (auto v : fe[t]) if (!fvis[v]) fvis[v] = 1, maxv[v] = val[u], q.push(v);
}
}
for (int i = 1; i <= n; ++i) {
if (!minv[i] || !maxv[i]) continue;
ans = max(ans, maxv[i]-minv[i]);
}
printf("%d\n", ans);
return 0;
}
深圳集训(7.25-7.31)
7.25(Day 1)
P1119 灾后重建:Floyd(绿)
每次加上当前重建完的村庄的边,Floyd 更新最短路。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 210, inf = 1e9;
int n, m, q, now, t[N];
int f[N][N];
void update(int k) { // 以k点为中转点,更新最短路
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j)
f[i][j] = f[j][i] = min(f[i][j], f[i][k]+f[k][j]);
}
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 0; i < n; ++i) scanf("%d", &t[i]);
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j)
f[i][j] = (i == j) ? 0 : inf;
}
for (int i = 0; i < m; ++i) {
int u, v, w; scanf("%d%d%d", &u, &v, &w);
f[u][v] = f[v][u] = min(f[u][v], w);
}
scanf("%d", &q);
while (q -- ) {
int x, y, d; scanf("%d%d%d", &x, &y, &d);
while (t[now] <= d && now < n) update(now), now ++;
if (t[x] > d || t[y] > d) puts("-1");
else printf("%d\n", (f[x][y]==inf)?-1:f[x][y]);
}
return 0;
}
P6688 可重集:(*)树状数组,hash(蓝)
我们需要在 \(\le O(\log n)\) 的时间复杂度内判断两个区间排序后是否相等,所以我们考虑用 Hash 来维护区间值。本题中我们取 \(hash(x)=p^x\)。
这个哈希函数有一个很好的性质:
同时注意到 \(k=\dfrac{\sum(a_i+k)-\sum a_i}{r-l+1}\),那么我们只需要用树状数组维护区间和及区间 hash 和即可。
时间复杂度 \(O(n\log n)\)。(本代码通过率较低)
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <chrono>
#include <random>
using namespace std;
#define int long long
const int N = 1e6+10;
int n, q, P, p, a[N][2];
int c[N][2];
int power(int a, int b) {
int res = 1;
while (b) {
if (b & 1) res = res * a % p;
a = a * a % p;
b >>= 1;
}
return res;
}
int lowbit(int x) {
return x & -x;
}
void add(int pos, int x, int type) {
for (int i = pos; i <= n; i += lowbit(i))
c[i][type] += x;
}
int query(int pos, int type) {
int sum = 0;
for (int i = pos; i >= 1; i -= lowbit(i))
sum += c[i][type];
return sum;
}
signed main() {
mt19937 gen(chrono::system_clock::now().time_since_epoch().count());
uniform_int_distribution<int>dist((int)2e6,(int)2.5e6); P = dist(gen), p = dist(gen); // 随机底数和模数
scanf("%lld%lld", &n, &q);
for (int i = 1; i <= n; ++i) {
scanf("%lld", &a[i][0]), a[i][1] = power(P, a[i][0]);
add(i, a[i][0], 0), add(i, a[i][1], 1);
}
int op;
while (q -- ) {
scanf("%lld", &op);
if (!op) {
int x, y; scanf("%lld%lld", &x, &y);
int t = power(P, y);
add(x, y-a[x][0], 0), add(x, t-a[x][1], 1);
a[x][0] = y, a[x][1] = t;
} else {
int l1, r1, l2, r2; scanf("%lld%lld%lld%lld", &l1, &r1, &l2, &r2);
int k = (query(r2, 0)-query(l2-1, 0)) - (query(r1, 0)-query(l1-1, 0));
if (k % (r1-l1+1) != 0) {puts("NO"); continue;}
k /= r1-l1+1;
if (k < 0) k = -k, swap(l1, l2), swap(r1, r2);
if (((query(r2, 1)-query(l2-1, 1))%p+p)%p == ((query(r1, 1)-query(l1-1, 1))*power(P, k)%p+p)%p) puts("YES");
else puts("NO");
}
}
return 0;
}
ABC200B. 200th ABC-200:模拟(红)
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
#define int long long
int n, k;
signed main() {
scanf("%lld%lld", &n, &k);
while (k) {
if (n % 200 == 0) n /= 200;
else n = n * 1000 + 200;
k --;
}
printf("%lld\n", n);
return 0;
}
ABC200C. Ringo's Favorite Numbers 2:桶(红)
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long ll;
int n, num[210];
ll ans;
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) {
int x; scanf("%d", &x); x %= 200;
ans += num[x], num[x] ++;
}
printf("%lld\n", ans);
return 0;
}
ABC201B. Do you know the second highest mountain?:排序(红)
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
typedef pair<int, string> pis;
int n;
pis m[1010];
int main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n;
for (int i = 1; i <= n; ++i) cin >> m[i].second >> m[i].first;
sort(m+1, m+n+1, greater<pis>());
cout << m[2].second << '\n';
return 0;
}
ABC281C. Secret Number:dfs(橙)
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
int cnt, num[15];
char s[15];
void dfs(int u) {
if (u == 4) {
for (int i = 0; i <= 9; ++i) {
if (s[i] == 'o' && !num[i])
return ;
}
cnt ++; return ;
}
for (int i = 0; i <= 9; ++i) {
if (s[i] == 'x') continue;
num[i] ++, dfs(u+1), num[i] --;
}
}
int main() {
cin >> s;
dfs(0);
printf("%d\n", cnt);
return 0;
}
ABC202C. Made Up:桶(红)
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long ll;
const int N = 1e5+10;
int n, a[N], b[N], c[N], num[N];
ll ans;
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%d", &a[i]), num[a[i]] ++;
for (int i = 1; i <= n; ++i) scanf("%d", &b[i]);
for (int i = 1; i <= n; ++i) scanf("%d", &c[i]);
for (int j = 1; j <= n; ++j) ans += num[b[c[j]]];
printf("%lld\n", ans);
return 0;
}
ABC199C. IPFL:字符串,模拟(橙)
注意到操作二后若 \(i\le n\),则 \(i\leftarrow n+i\),否则 \(i\leftarrow i-n\)。用一个 bool 变量存储当前翻转的次数,若为偶数次则无影响,若为奇数次则要对 \(a,b\) 作相应的变换。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 4e5+10;
int n, q; bool flip;
char s[N];
int main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
int op, a, b;
cin >> n >> s+1 >> q;
while (q -- ) {
cin >> op >> a >> b;
if (op == 1) {
if (flip) a = (a <= n) ? n+a : a-n, b = (b <= n) ? n+b : b-n;
swap(s[a], s[b]);
}
else flip ^= 1;
}
if (flip) for (int i = 1; i <= n; ++i) swap(s[i], s[i+n]);
for (int i = 1; i <= 2*n; ++i) cout << s[i];
return 0;
}
ABC200E. Patisserie ABC 2:(*)数学,排列组合,容斥原理(蓝)
令 \(get(x)\) 表示 \(i+j+k=x\) 时(不考虑 \(n\) 的限制)的三元组 \((i,j,k)\) 的数量。通过插板法,可得 \(get(x)=\dfrac{(x-1)(x-2)}{2}\)。
我们首先枚举 \(x\),考虑有多少个满足 \(i+j+k=x\) 且 \(1\le i,j,k\le n\) 的三元组。我们可以将 \(get(x)\) 中的方案数分为 \(4\) 类:\(i,j,k\) 均 \(\le n\)、恰好有一个 \(> n\)、恰好有两个 \(>n\)、恰好有三个 \(>n\)。先减去 \(i,j,k\) 中至少有一个数 \(>n\) 的方案数 \(3\cdot get(x-n)\);但这样又多减去了至少有两个数 \(>n\) 的方案数 \(3\cdot get(x-2n)\),需要补上;最后还需要减去三个数 \(>n\) 的方案数 \(get(x-3n)\)。
得到 \(i+j+k\) 的范围后,枚举 \(i\) 计算即可。
时间复杂度 \(O(n)\)。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
#define int long long
int n, m;
int get(int x) {
if (x <= 2) return 0; // 和至少为3
return (x-1) * (x-2) / 2;
}
signed main() {
scanf("%lld%lld", &n, &m);
for (int x = 3; x <= 3*n; ++x) {
int num = get(x) - 3*get(x-n) + 3*get(x-2*n) - get(x-3*n);
if (m > num) {m -= num; continue;}
for (int i = 1; i <= n; ++i) {
int Min = max(x-i-n, 1ll), Max = min(x-i-1, n);
// Min, Max表示j当前的最小/最大值
if (Min > Max) continue;
num = Max - Min + 1;
if (m > num) {m -= num; continue;}
int j = Min + m - 1, k = x-i-j;
printf("%lld %lld %lld\n", i, j, k);
return 0;
}
}
return 0;
}
ABC202D. aab aba baa:全排列,数学(黄)
假设当前还剩下 \(a\) 个 a,\(b\) 个 b,那么当前位以 a 开头的数的个数为 \(\dbinom{a+b-1}{a-1}\)。若 \(k\) 小于这个值说明这一位为 a,否则说明这一位为 \(b\),减去以 a 开头的数个数。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
#define int long long
int a, b, k, cnta, cntb;
int c[65][65];
void solve(int digit) {
if (digit == a+b) return ;
int num = c[a+b-cnta-cntb-1][a-cnta-1];
if (k > num) k -= num;
else {cnta ++, putchar('a'), solve(digit+1); return ;}
num = c[a+b-cnta-cntb-1][b-cntb-1];
if (k > num) k -= num;
cntb ++, putchar('b');
solve(digit+1);
return ;
}
signed main() {
scanf("%lld%lld%lld", &a, &b, &k);
c[0][0] = 1;
for (int i = 1; i <= 60; ++i) {
c[i][0] = c[i][i] = 1;
for (int j = 1; j <= i/2; ++j)
c[i][j] = c[i][i-j] = c[i-1][j]+c[i-1][j-1];
}
solve(0);
return 0;
}
ABC201D. Game in Momotetsu World:博弈论,dp(绿)
令 \(f_{i,j}\) 表示走到 \((i,j)\) 时,先后手的最大得分差。先手的目标是最大化 \(f_{i,j}\),后手的目标是最小化 \(f_{i,j}\)。可以发现,走到 \((i,j)\) 时,若 \(i+j\bmod 2=0\) 则先手走,否则后手走。那么我们可以列出状态转移方程:
可以采用记忆化搜索实现。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 2010, inf = 1e9;
int n, m;
int a[N][N], f[N][N];
int dfs(int x, int y) {
if (f[x][y] != -inf) return f[x][y];
if (x == n && y == m) return f[x][y] = 0;
if ((x+y) % 2) {
f[x][y] = inf;
if (x+1 <= n) f[x][y] = min(f[x][y], dfs(x+1, y)-a[x+1][y]);
if (y+1 <= m) f[x][y] = min(f[x][y], dfs(x, y+1)-a[x][y+1]);
} else {
f[x][y] = -inf;
if (x+1 <= n) f[x][y] = max(f[x][y], dfs(x+1, y)+a[x+1][y]);
if (y+1 <= m) f[x][y] = max(f[x][y], dfs(x, y+1)+a[x][y+1]);
}
return f[x][y];
}
int main() {
cin >> n >> m;
for (int i = 1; i <= n; ++i) {
string s; cin >> s;
for (int j = 0; j < s.size(); ++j) a[i][j+1] = (s[j] == '+') ? 1 : -1, f[i][j+1] = -inf;
}
int ans = dfs(1, 1);
if (ans > 0) puts("Takahashi");
else if (!ans) puts("Draw");
else puts("Aoki");
return 0;
}
7.26(Day 2)
P4799 [CEOI2015 Day2] 世界冰球锦标赛:折半搜索(meet in the middle)(绿)
显然直接搜索或者 dp 都会爆炸。注意到 \(1\le n\le 40\),这是折半搜索的经典复杂度。
普通搜索的时间复杂度为 \(O(2^n)\),而折半搜索的时间复杂度为 \(O(2^{n/2}+\text{合并的时间复杂度})\)。
我们可以将序列划分为 \([1,n/2]\) 和 \([n/2+1, n]\) 两个部分,分别进行搜索,将答案分别存储在两个 vector \(A, B\) 中。合并时,我们先将 \(A\) 排序,对于后半部分的一个代价 \(B_i\),二分找到最后一个 \(\le B_i\) 的数 \(A_j\),则 \(B_i\) 对答案的贡献即为 \(j\)。
时间复杂度 \(O(2^{n/2}+n\log n)\)。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <vector>
using namespace std;
#define int long long
const int N = 45;
int n, m, ans, a[N];
vector<int> A, B;
void dfs(int L, int R, int sum, vector<int> &T) {
if (sum > m) return ;
if (L > R) { // 该部分已搜索完
T.push_back(sum);
return ;
}
dfs(L+1, R, sum+a[L], T), dfs(L+1, R, sum, T); // 选/不选
}
signed main() {
scanf("%lld%lld", &n, &m);
for (int i = 1; i <= n; ++i) scanf("%lld", &a[i]);
dfs(1, n/2, 0, A), dfs(n/2+1, n, 0, B);
sort(A.begin(), A.end());
for (int i = 0; i < B.size(); ++i) ans += upper_bound(A.begin(), A.end(), m-B[i]) - A.begin(); // 合并答案
printf("%lld\n", ans);
return 0;
}
ABC184F. Programming Contest:折半搜索(绿)
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
#define int long long
const int N = 40;
int n, m, ans, a[N];
vector<int> A, B;
void dfs(int L, int R, int sum, vector<int> &T) {
if (sum > m) return ;
if (L > R) {
T.push_back(sum);
return ;
}
dfs(L+1, R, sum+a[L], T), dfs(L+1, R, sum, T);
}
signed main() {
scanf("%lld%lld", &n, &m);
for (int i = 1; i <= n; ++i) scanf("%lld", &a[i]);
dfs(1, n/2, 0, A), dfs(n/2+1, n, 0, B);
sort(A.begin(), A.end());
for (int i = 0; i < B.size(); ++i) {
int x = A[upper_bound(A.begin(), A.end(), m-B[i])-A.begin()-1];
ans = max(ans, B[i]+x);
}
printf("%lld\n", ans);
return 0;
}
ABC201E. Xor Distances:位运算,dfs(绿)
令 \(val_i\) 表示从 \(1\) 号点到 \(i\) 号点的边权异或和。从 \(i\) 到 \(j\) 的路径上的边权异或和显然为 \(\left(val_i\oplus val_{\text{lca}(i,j)}\right)\oplus \left(val_j\oplus val_{\text{lca}(i,j)}\right)=val_i\oplus val_j\)。注意到异或只会对当前位产生影响,那么我们枚举每个二进制位,若 \(val\) 中第 \(i\) 位上有 \(x\) 个 \(1\),则第 \(i\) 位对答案的贡献为 \(2^{i-1}x(n-x)\)。
时间复杂度 \(O(n\log V)\)。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <vector>
using namespace std;
#define int long long
typedef pair<int, int> pii;
const int N = 2e5+10, P = 1e9+7;
int n, ans, val[N];
vector<pii> e[N];
void dfs(int u, int fa) {
for (auto edge : e[u]) {
int v = edge.first, w = edge.second;
if (v == fa) continue;
val[v] = val[u] ^ w; dfs(v, u);
}
}
signed main() {
scanf("%lld", &n);
for (int i = 1; i < n; ++i) {
int u, v, w; scanf("%lld%lld%lld", &u, &v, &w);
e[u].push_back({v, w}), e[v].push_back({u, w});
}
dfs(1, 1);
for (int i = 0; i < 60; ++i) {
int cnt0 = 0, cnt1 = 0;
for (int j = 1; j <= n; ++j) (val[j] >> i & 1) ? cnt1 ++ : cnt0 ++;
ans = (ans + (__int128)(1ll<<i) * cnt0 % P * cnt1 % P) % P;
}
printf("%lld\n", ans);
return 0;
}
P5367 【模板】康托展开:全排列,数学,树状数组(绿)
首先我们有一个式子:
其中,\(count_i=\sum_{j=i}^n[a_i>a_j]\),即 \(i\) 后面比 \(a_i\) 小的数的个数,可以用树状数组计算。这里我们需要用到一个技巧,\(1\sim n\) 中比 \(i\) 小的数量是 \(i-1\),那么我们只需要知道 \(i\) 前面比 \(a_i\) 小的个数即可。
枚举到第 \(i\) 个数时,表示已经确定前 \(i-1\) 位,第 \(i\) 位与 \(a_i\) 不同的全排列数量。
时间复杂度 \(O(n\log n)\),需要预处理阶乘。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long ll;
const int N = 1e6+10, P = 998244353;
int n, ans = 1, a[N], c[N], fac[N];
int lowbit(int x) {
return x & -x;
}
void add(int x, int k) {
for (int i = x; i <= n; i += lowbit(i))
c[i] += k;
}
int query(int x) {
int sum = 0;
for (int i = x; i >= 1; i -= lowbit(i))
sum += c[i];
return sum;
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
fac[0] = 1;
for (int i = 1; i <= n; ++i) fac[i] = (ll)fac[i-1] * i % P;
for (int i = 1; i <= n; ++i) ans = (ans + (ll)(a[i]-query(a[i])-1) * fac[n-i] % P) % P, add(a[i], 1);
printf("%d\n", ans);
return 0;
}
Codeforces Round 888 (Div. 3):solve 5/7 rk 592
CF1851A. Escalator Conversations:模拟(红)
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 55;
int t, n, m, k, h, a[N];
int main() {
scanf("%d", &t);
while (t -- ) {
int ans = 0;
scanf("%d%d%d%d", &n, &m, &k, &h);
for (int i = 1; i <= n; ++i) {
scanf("%d", &a[i]);
int H = abs(a[i]-h);
if (H && H % k == 0 && H / k < m) ans ++;
}
printf("%d\n", ans);
}
return 0;
}
CF1851B. Parity Sort:贪心(橙)
将奇偶数分别排序,判断是否能构成不下降序列。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 2e5+10;
int t, n, a[N];
int main() {
scanf("%d", &t);
while (t -- ) {
vector<int> A, B; bool check = 1;
scanf("%d", &n);
for (int i = 1; i <= n; ++i) {
scanf("%d", &a[i]);
if (a[i] % 2 == 0) A.push_back(a[i]);
else B.push_back(a[i]);
}
sort(A.begin(), A.end(), greater<int>()), sort(B.begin(), B.end(), greater<int>());
for (int i = 1; i <= n; ++i) {
if (a[i] % 2 == 0) a[i] = A[A.size()-1], A.pop_back();
else a[i] = B[B.size()-1], B.pop_back();
if (a[i] < a[i-1]) {check = 0; break;}
}
(check) ? puts("YES") : puts("NO");
}
return 0;
}
CF1851C. Tiles Comeback:贪心(黄)
可以想到,段数为 \(2\) 一定是最容易满足的。那么令 \(a_1\) 往后跳 \(k\) 次跳到的的最小砖块为 \(x\),\(a_n\) 往前跳 \(k\) 次的最大砖块为 \(y\),若 \(x<y\) 则满足题意。注意特判 \(a_1=a_n\) 的情况。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 2e5+10;
int t, n, k, a[N];
int main() {
scanf("%d", &t);
while (t -- ) {
scanf("%d%d", &n, &k);
for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
vector<int> A, B;
for (int i = 1; i <= n; ++i) {
if (a[i] == a[1]) A.push_back(i);
if (a[i] == a[n]) B.push_back(i);
}
if (A.size() < k) {puts("NO"); continue;}
int t = lower_bound(B.begin(), B.end(), A[k-1]) - B.begin();
if (B.size()-t >= k || a[1] == a[n]) puts("YES");
else puts("NO");
}
return 0;
}
CF1851D. Prefix Permutation Sums:差分,桶(黄)
令 \(b_i=a_i-a_{i-1}\),将其存入桶中。若 \(b_i\) 已出现或 \(b_i>n\),说明 \(b_i\) 是由两数合成的。再找到 \(1\sim n\) 排列中未出现的两个数 \(x,y\),若 \(x+y=b_i\) 或没有不合法的数(说明最后一个数是合成的)则答案为 YES;否则若有两个需要合成的数或 \(x+y\ne b_i\) 则答案为 NO。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
#define int long long
const int N = 2e5+10;
int t, n, a[N], b[N], col[N];
signed main() {
scanf("%lld", &t);
while (t -- ) {
memset(col, 0, sizeof col);
int sum = 0; bool check = 1;
scanf("%lld", &n);
for (int i = 1; i < n; ++i) {
scanf("%lld", &a[i]), b[i] = a[i] - a[i-1];
if ((b[i] > n || col[b[i]]) && sum) check = 0;
else if (b[i] <= n && !col[b[i]]) col[b[i]] ++;
else sum = b[i];
}
if (!check) {puts("NO"); continue;}
int tot = 0;
for (int i = 1; i <= n; ++i) {
if (!col[i])
tot += i;
}
if (tot == sum || !sum) puts("YES");
else puts("NO");
}
return 0;
}
CF1851E. Nastya and Potions:拓扑排序,dp(绿)
由于一个药剂不能通过有限次操作合成自己,所以是一个 DAG。
令 \(f_u\) 表示药剂 \(u\) 的最小花费,若初始时药剂 \(u\) 已拥有则 \(f_u=0\),否则 \(f_u=+\infty\)。则状态转移方程为:
按拓扑序 dp 即可。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <queue>
using namespace std;
#define int long long
const int N = 2e5+10, inf = 1e18;
int t, n, k, c[N], f[N]; bool h[N];
int deg[N];
vector<int> e[N];
void bfs() {
queue<int> q;
for (int i = 1; i <= n; ++i) if (!deg[i]) q.push(i);
while (q.size()) {
int u = q.front(); q.pop();
f[u] = min(f[u], (h[u])?0:c[u]);
for (auto v : e[u]) {
if (f[v] == inf) f[v] = 0;
f[v] += f[u], deg[v] --;
if (!deg[v]) q.push(v);
}
}
}
signed main() {
scanf("%lld", &t);
while (t -- ) {
scanf("%lld%lld", &n, &k); memset(h, 0, sizeof h);
for (int i = 1; i <= n; ++i) e[i].clear(), f[i] = inf;
for (int i = 1; i <= n; ++i) scanf("%lld", &c[i]);
for (int i = 1; i <= k; ++i) {int x; scanf("%lld", &x), h[x] = 1;}
for (int i = 1; i <= n; ++i) {
scanf("%lld", °[i]);
for (int j = 1; j <= deg[i]; ++j) {int x; scanf("%lld", &x), e[x].push_back(i);}
}
bfs();
for (int i = 1; i <= n; ++i) printf("%lld ", f[i]);
puts("");
}
return 0;
}
CF1851F. Lisa and the Martians:01 Trie,贪心(绿)
由于每一位都是独立的,对于 \(a_i\) 和 \(a_j\) 的某一二进制位:
- 均为 \(1\):\(x\) 的这一位应为 \(0\),\(ans\) 的这一位就是 \(1\);
- 均为 \(0\):\(x\) 的这一位应为 \(1\),\(ans\) 的这一位就是 \(1\);
- 为 \(0,1\):\(x\) 的这一位为 \(0\) 或 \(1\) 均可,\(ans\) 的这一位只能为 \(0\)。
可以发现,我们需要让 \(a_i\) 和 \(a_j\) 从高位到低位相同的二进制位数尽量多,考虑用 Trie 维护。
注意清空不能直接用 memset。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 2e5+10, M = 6e6+10;
int t, n, k, a[N];
int son[M][2], last[M], idx;
void insert(int x, int pos) {
int p = 0;
for (int i = k; i >= 0; --i) {
int s = x >> i & 1;
if (!son[p][s]) son[p][s] = ++ idx; p = son[p][s];
}
last[p] = pos;
}
int query(int x) {
int p = 0;
for (int i = k; i >= 0; --i) {
int s = x >> i & 1;
if (son[p][s]) p = son[p][s]; else p = son[p][!s];
}
return last[p];
}
void del(int p) {
if (son[p][0]) del(son[p][0]);
if (son[p][1]) del(son[p][1]);
last[p] = son[p][0] = son[p][1] = 0;
}
int main() {
scanf("%d", &t);
while (t -- ) {
int X, Y, tot, ans; X = Y = tot = idx = 0, ans = -1;
scanf("%d%d", &n, &k);
for (int i = 1; i <= n; ++i) {
scanf("%d", &a[i]);
if (i > 1) {
int pos = query(a[i]), x = 0;
for (int j = 0; j < k; ++j) {
int tmp1 = a[i] >> j & 1, tmp2 = a[pos] >> j & 1;
if (!tmp1 && !tmp2) x += 1 << j;
}
if (((a[i]^x)&(a[pos]^x)) > ans) ans = (a[i]^x)&(a[pos]^x), X = pos, Y = i, tot = x;
}
insert(a[i], i);
}
printf("%d %d %d\n", X, Y, tot);
del(0);
}
return 0;
}
7.27(Day 3)
P2986 [USACO10MAR] Great Cow Gathering G:换根 dp(蓝)
令 \(siz_i\) 表示以 \(i\) 为根节点的子树内奶牛的数量,\(f_i\) 表示以 \(i\) 作为集会地点时的不方便程度,则状态转移方程为:
注意初始时 \(f_1=\sum_{i=1}^n c_id_i\)。其中 \(d_i\) 表示 \(1\) 号点到 \(i\) 号点的距离。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <vector>
using namespace std;
typedef pair<int, int> pii;
typedef long long ll;
const int N = 1e5+10;
int n, sum, c[N]; ll ans = 1e18, f[N], siz[N], dist[N];
vector<pii> e[N];
void dfs(int u, int fa) {
siz[u] = c[u], f[1] += dist[u] * c[u];
for (auto edge : e[u]) {
int v = edge.first, w = edge.second;
if (v == fa) continue;
dist[v] = dist[u]+w, dfs(v, u), siz[u] += siz[v];
}
}
void dp(int u, int fa) {
ans = min(ans, f[u]);
for (auto edge : e[u]) {
int v = edge.first, w = edge.second;
if (v == fa) continue;
f[v] = f[u] - siz[v] * w + (sum-siz[v]) * w, dp(v, u);
}
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%d", &c[i]), sum += c[i];
for (int i = 1; i < n; ++i) {
int u, v, w; scanf("%d%d%d", &u, &v, &w);
e[u].push_back({v, w}), e[v].push_back({u, w});
}
dfs(1, 1), dp(1, 1);
printf("%lld\n", ans);
return 0;
}
P3047 [USACO12FEB] Nearby Cows G:(*)换根 dp(蓝)
令 \(f_{i,j}\) 表示在以 \(i\) 为根节点的子树内,深度为 \(j\) 的点的点权之和(只有在 \(u\) 为根节点时,\(f_{u,j}\) 才为真实值)。初始时以 \(1\) 号点为根节点,\(f_{u,j}=\displaystyle\sum_{(u,v)\in E} f_{v,j-1}\)。

如上图,观察根从 \(u\) 转移到 \(v\) 时,\(f_{u,j}\) 和 \(f_{v,j}\) 发生的变化。可以发现,由于 \(u\) 已经不再是根节点,所以 \(f_{u,j}\leftarrow f_{u,j}-f_{v,j-1}\);而 \(v\) 成为了新的根节点,\(f_{v,j}\leftarrow f_{v,j}+f_{u,j-1}\)。依次计算答案即可,注意回溯时要再把根转移回 \(u\)。
时间复杂度 \(O(nk)\)。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 1e5+10;
int n, k, c[N], f[N][25], ans[N];
vector<int> e[N];
void dfs(int u, int fa) {
f[u][0] = c[u];
for (auto v : e[u]) {
if (v == fa) continue;
dfs(v, u);
for (int i = 1; i <= k; ++i) f[u][i] += f[v][i-1];
}
}
void trans(int u, int v) {
for (int i = 1; i <= k; ++i) f[u][i] -= f[v][i-1];
for (int i = 1; i <= k; ++i) f[v][i] += f[u][i-1];
}
void dp(int u, int fa) {
for (int i = 0; i <= k; ++i) ans[u] += f[u][i];
for (auto v : e[u]) {
if (v == fa) continue;
trans(u, v), dp(v, u), trans(v, u);
}
}
int main() {
scanf("%d%d", &n, &k);
for (int i = 1; i < n; ++i) {
int u, v; scanf("%d%d", &u, &v);
e[u].push_back(v), e[v].push_back(u);
}
for (int i = 1; i <= n; ++i) scanf("%d", &c[i]);
dfs(1, 1), dp(1, 1);
for (int i = 1; i <= n; ++i) printf("%d\n", ans[i]);
return 0;
}
7.29(Day 5)
CF906D. Power Tower:奈芙莲树,树状数组,扩展欧拉定理(紫)
P3934 [Ynoi2016] 炸脖龙 I 的双倍经验,注意此题 \(p\le 10^9\) 且初始时已给定,我们需要预处理出 \(\varphi(p),\varphi(\varphi(p)),\cdots\)。
点击查看代码
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <unordered_map>
using namespace std;
#define int long long
const int N = 5e5+10, M = 2e7+10;
int n, m, p, c[N];
unordered_map<int, int> phi;
int get_euler(int x) {
int ans = x;
for (int i = 2; i <= x/i; ++i) {
bool check = 0;
while (x % i == 0) {
x /= i;
check = 1;
}
if (check) ans = ans / i * (i-1);
}
if (x > 1) ans = ans / x * (x-1);
return ans;
}
int lowbit(int x) {
return x & -x;
}
void add(int pos, int x) {
for (int i = pos; i <= n; i += lowbit(i))
c[i] += x;
}
int query(int pos) {
int sum = 0;
for (int i = pos; i >= 1; i -= lowbit(i))
sum += c[i];
return sum;
}
struct Node {
int v; bool flag; // v存储值, flag存储是否>=p
Node (int v = 0, bool flag = false) : v(v), flag(flag) {}
};
Node power(int a, int b, int p) { // 在快速幂的过程中判断是否>=p
Node res = Node(1, 0);
if (a >= p) a %= p, res.flag = 1;
while (b) {
if (b & 1) res.v *= a;
if (res.v >= p) res.flag = 1, res.v %= p;
a *= a;
if (a >= p) res.flag = 1, a %= p;
b >>= 1;
}
return res;
}
Node solve(int l, int r, int p) {
int L = query(l);
if (p == 1) return Node(0, 1);
if (L == 1) return Node(1, 0);
if (l == r) return (L<p) ? Node(L, 0) : Node(L%p, 1);
Node res = solve(l+1, r, phi[p]);
if (res.flag) res.v += phi[p]; // 如果>=p,根据扩展欧拉定理指数还需要加上phi[p]
return power(L, res.v, p);
}
signed main() {
scanf("%lld%lld", &n, &p);
int tmp = p;
while (p != 1) {
int t = get_euler(p);
phi[p] = t, p = t;
}
p = tmp;
for (int i = 1; i <= n; ++i) {
int x; scanf("%lld", &x);
add(i, x), add(i+1, -x);
}
int l, r;
scanf("%lld", &m);
while (m -- ) {
scanf("%lld%lld", &l, &r);
printf("%lld\n", solve(l, r, p).v);
}
return 0;
}
P5138 fibonacci:斐波那契数列,线段树,树链剖分,数学(黑)
首先我们有一个重要的式子:
证明:
\(m=0\) 时,显然有 \(f_nf_1+f_{n-1}f_0=f_n\)。
假设 \(\forall m\in [0,k],m\in \mathbb{N}\) 结论成立,则 \(m=k+1\) 时,有:
\[\begin{aligned} f_{n}f_{k+2}+f_{n-1}f_{k+1} &= f_nf_{k+1}+f_{n}f_{k}+f_{n-1}f_{k+1} \\ &= (f_{n-1}f_{k}+f_{n}f_{k+1})+(f_{n-2}f_{k}+f_{n-1}f_{k+1}) \\ &= f_{n+k}+f_{n+k-1} \\ &= f_{n+k+1} \end{aligned} \]
假设我们要计算 \(u\) 的子树内的一个节点 \(v\) 的增加量,则有:
注意到 \(k-dep_u\) 可能小于 \(0\),我们有 \(f_{-n}=(-1)^{n-1}f_n\),可以证明其仍然满足上面的式子(因为递推式 \(f_n=f_{n-1}+f_{n-2}\) 仍然成立)。
由于 \(f_{dep_v},f_{dep_{v-1}}\) 均为常数,我们可以线段树维护两个常数 \(\sum f_{dep_v},\sum{f_{dep_v-1}}\),两个增加量 \(\sum f_{k-dep_u+1}, \sum f_{k-dep_u}\) 以及节点的增加量之和。
树链剖分后用线段树维护即可。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <vector>
using namespace std;
#define int long long
typedef long long ll;
typedef pair<ll, ll> pii;
const int N = 2e5+10, P = 1e9+7;
int n, m;
vector<int> e[N];
struct Matrix {
int num[4][4];
Matrix() {
memset(num, 0, sizeof num);
}
};
Matrix operator *(const Matrix &a, const Matrix &b) {
Matrix ans;
for (int k = 1; k <= 2; ++k) {
for (int i = 1; i <= 2; ++i)
for (int j = 1; j <= 2; ++j)
ans.num[i][j] = (ans.num[i][j] + (ll)a.num[i][k] * b.num[k][j]) % P;
}
return ans;
}
Matrix power(Matrix &a, int b) {
Matrix ans; for (int i = 1; i <= 2; ++i) ans.num[i][i] = 1;
while (b > 0) {
if (b & 1) ans = ans * a;
a = a * a;
b >>= 1;
}
return ans;
}
int calc(ll k) {
int f = 1;
if (k < 0) k = -k, f = (k % 2) ? 1 : -1;
if (k == 0) return 0;
Matrix a, trans;
a.num[1][1] = a.num[1][2] = 1; trans.num[1][1] = trans.num[1][2] = trans.num[2][1] = 1;
Matrix ans = a;
if (k >= 2) ans = ans * power(trans, k-2);
return (f*ans.num[1][1]%P+P)%P;
}
int idx, id[N], dfn[N];
int dep[N], siz[N], top[N], son[N], f[N];
void get_son(int u, int fa) {
siz[u] = 1, dep[u] = dep[fa]+1, f[u] = fa;
for (auto v : e[u]) {
if (v == fa) continue;
get_son(v, u), siz[u] += siz[v];
if (siz[v] > siz[son[u]]) son[u] = v;
}
}
void get_top(int u, int t) {
top[u] = t, id[u] = ++ idx, dfn[idx] = u;
if (son[u]) get_top(son[u], t);
for (auto v : e[u]) {
if (v == f[u] || v == son[u]) continue;
get_top(v, v);
}
}
struct Node {
int l, r, sum; pii val, tag;
} seg[N<<2];
void pushup(int u) {
seg[u].val.first = (seg[u<<1].val.first + seg[u<<1|1].val.first) % P;
seg[u].val.second = (seg[u<<1].val.second + seg[u<<1|1].val.second) % P;
seg[u].sum = (seg[u<<1].sum + seg[u<<1|1].sum) % P;
}
void pushdown(Node &u, Node &now) {
now.sum = (now.sum + (ll)now.val.first*u.tag.first%P + (ll)now.val.second*u.tag.second%P) % P;
now.tag.first = ((ll)now.tag.first + u.tag.first) % P;
now.tag.second = ((ll)now.tag.second + u.tag.second) % P;
}
void pushdown(int u) {
pushdown(seg[u], seg[u<<1]), pushdown(seg[u], seg[u<<1|1]);
seg[u].tag = make_pair(0, 0);
}
void build(int u, int l, int r) {
seg[u].l = l, seg[u].r = r, seg[u].tag = make_pair(0, 0);
if (l == r) seg[u].val.first = calc(dep[dfn[l]]), seg[u].val.second = calc(dep[dfn[l]]-1);
else {
int mid = l + r >> 1;
build(u<<1, l, mid), build(u<<1|1, mid+1, r);
pushup(u);
}
}
int query(int u, int l, int r) {
if (seg[u].l >= l && seg[u].r <= r) return seg[u].sum;
pushdown(u);
int mid = seg[u].l + seg[u].r >> 1, ans = 0;
if (l <= mid) ans = ((ll)ans + query(u<<1, l, r)) % P;
if (r > mid) ans = ((ll)ans + query(u<<1|1, l, r)) % P;
return ans;
}
void modify(int u, int l, int r, ll val1, ll val2) {
if (seg[u].l >= l && seg[u].r <= r) {
Node tmp; tmp.tag = make_pair(val1, val2);
pushdown(tmp, seg[u]);
return ;
}
pushdown(u);
int mid = seg[u].l + seg[u].r >> 1;
if (l <= mid) modify(u<<1, l, r, val1, val2);
if (r > mid) modify(u<<1|1, l, r, val1, val2);
pushup(u);
return ;
}
int ask_path(int u, int v) {
int sum = 0;
while (top[u] != top[v]) {
if (dep[top[u]] < dep[top[v]]) swap(u, v);
sum = ((ll)sum+query(1, id[top[u]], id[u])) % P;
u = f[top[u]];
}
if (dep[u] > dep[v]) swap(u, v);
sum = ((ll)sum + query(1, id[u], id[v])) % P;
return sum;
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m;
for (int i = 1; i < n; ++i) {
int u, v; cin >> u >> v;
e[u].push_back(v), e[v].push_back(u);
}
get_son(1, 1), get_top(1, 1);
build(1, 1, n);
char op; int x; ll y;
for (int i = 1; i <= m; ++i) {
cin >> op >> x >> y;
if (op == 'U') modify(1, id[x], id[x]+siz[x]-1, calc(y-dep[x]+1), calc(y-dep[x]));
else cout << ask_path(x, y) << '\n';
}
return 0;
}
ABC203D. Pond:二维前缀和,二分(绿)
二分答案 \(x\),将正方形内所有 \(\le x\) 的数都置为 \(1\),其余置为 \(0\),枚举每个边长为 \(k\) 的正方形内是否有 \(\ge \left\lceil\dfrac{k^2}{2}\right\rceil\) 个 \(\le x\) 的数。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 850;
int n, k, a[N][N], s[N][N];
bool check(int x) {
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= n; ++j)
s[i][j] = s[i-1][j] + s[i][j-1] - s[i-1][j-1] + (a[i][j] <= x);
}
for (int i = 1; i <= n-k+1; ++i) {
for (int j = 1; j <= n-k+1; ++j) {
int num = s[i+k-1][j+k-1] - s[i-1][j+k-1] - s[i+k-1][j-1] + s[i-1][j-1];
if (num >= k*k/2+(k%2)) return 1;
}
}
return 0;
}
int main() {
scanf("%d%d", &n, &k);
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= n; ++j)
scanf("%d", &a[i][j]);
}
int l = 0, r = 1000000000;
while (l < r) {
int mid = l + r >> 1;
if (check(mid)) r = mid;
else l = mid+1;
}
printf("%d\n", l);
return 0;
}
CF1763C. Another Array Problem:贪心,构造,分讨(绿)
注意到一个关键的性质:对一个区间进行两次操作后,该区间内的数会全部变为 \(0\)。
\(n=2\) 时,显然答案为 \(\max(a_1+a_2,2|a_1-a_2|)\)。
\(n=3\) 时,显然最后答案要么是 \(a_1+a_2+a_3\),要么是三个相同的数,则答案为 \(\max(a_1+a_2+a_3, 3a_1,3a_3,3|a_1-a_2|,3|a_3-a_2|)\)。
\(n\ge 4\) 时,显然可以通过若干次操作使得所有数都变为 \(\max\{a_i\}\)。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long ll;
const int N = 2e5+10;
int t, n, a[N]; ll maxl, sum;
int main() {
scanf("%d", &t);
while (t -- ) {
maxl = sum = 0;
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%d", &a[i]), sum += a[i], maxl = max(maxl, (ll)a[i]);
if (n == 2) printf("%lld\n", max(sum, 2ll*abs(a[2]-a[1])));
else if (n >= 4) printf("%lld\n", n*maxl);
else printf("%lld\n", max(sum, 3ll*max(max(a[1], a[3]), max(abs(a[2]-a[1]), abs(a[3]-a[2])))));
}
return 0;
}
7.30 (Day 6)
ABC312:solve 4/8,rk 2462
ABC312A. Chord:枚举(红)
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
string s[100] = {"ACE", "BDF", "CEG", "DFA", "EGB", "FAC", "GBD"};
int main() {
string S; cin >> S;
for (int i = 0; i < 7; ++i) {
if (S == s[i])
puts("Yes"), exit(0);
}
puts("No");
}
ABC312B. TaK Code:枚举(红)
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 110;
int n, m;
char s[N][N];
int main() {
cin >> n >> m;
for (int i = 1; i <= n; ++i) cin >> s[i] + 1;
for (int i = 1; i <= n-8; ++i) {
for (int j = 1; j <= m-8; ++j) {
if (s[i][j] == '#' && s[i][j+1] == '#' && s[i][j+2] == '#' &&
s[i+1][j] == '#' && s[i+1][j+1] == '#' && s[i+1][j+2] == '#' &&
s[i+2][j+1] == '#' && s[i+2][j+2] == '#' && s[i+2][j] == '#' &&
s[i+6][j+6] == '#' && s[i+6][j+7] == '#' && s[i+6][j+8] == '#' &&
s[i+7][j+7] == '#' && s[i+7][j+6] == '#' && s[i+7][j+8] == '#' &&
s[i+8][j+6] == '#' && s[i+8][j+7] == '#' && s[i+8][j+8] == '#' &&
s[i][j+3] == '.' && s[i+1][j+3] == '.' && s[i+2][j+3] == '.' && s[i+3][j+3] == '.' &&
s[i+3][j] == '.' && s[i+3][j+1] == '.' && s[i+3][j+2] == '.' &&
s[i+5][j+5] == '.' && s[i+5][j+6] == '.' && s[i+5][j+7] == '.' && s[i+5][j+8] == '.' &&
s[i+6][j+5] == '.' && s[i+7][j+5] == '.' && s[i+8][j+5] == '.')
printf("%d %d\n", i, j);
}
}
}
ABC312C. Invisible Hand:二分(橙)
二分答案后直接暴力枚举即可。时间复杂度 \(O(n\log n)\)。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 2e5+10;
int n, m;
int a[N], b[N];
bool cmp(int a, int b) {
return a > b;
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
for (int i = 1; i <= m; ++i) scanf("%d", &b[i]);
int l = 0, r = 1e9+10;
while (l < r) {
int mid = l + r >> 1;
int countA = 0, countB = 0;
for (int i = 1; i <= n; ++i) if (a[i] <= mid) countA ++;
for (int i = 1; i <= m; ++i) if (b[i] >= mid) countB ++;
if (countA < countB) l = mid+1;
else r = mid;
}
cout << l << '\n';
}
ABC312D. Count Bracket Sequences:dp(黄)
令 \(f_{i,j}\) 表示考虑前 \(i\) 个字符,存在 \(j\) 个左括号的方案数。初始时 \(f_{0,0}=1\)。显然状态转移方程为:
答案为 \(f_{n,n/2}\)。时间复杂度 \(O(n^2)\)。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
typedef long long ll;
const int N = 3010, P = 998244353;
int n, f[N][N];
char s[N];
int main() {
cin >> s+1; n = strlen(s+1);
f[0][0] = 1;
for (int i = 1; i <= n; ++i) {
for (int j = (i+1)/2; j <= min(i, n/2); ++j) {
if (s[i] == '(') f[i][j] = f[i-1][j-1];
else if (s[i] == ')') f[i][j] = f[i-1][j];
else f[i][j] = ((ll)f[i-1][j] + f[i-1][j-1]) % P;
}
}
cout << f[n][n/2] << '\n';
}
ABC312E. Tangency of Cuboids:模拟(黄)
对一个长方体内的所有小正方体打上标记,直接模拟即可。注意细节。
时间复杂度 \(O(m^2\log n)\)。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <map>
using namespace std;
const int N = 1e5+10;
const int dx[] = {-1, 1, 0, 0, 0, 0}, dy[] = {0, 0, -1, 1, 0, 0}, dz[] = {0, 0, 0, 0, -1, 1};
int n, ans[N];
map<pair<int, int>, bool> st;
int rec[110][110][110];
int main() {
scanf("%d", &n);
for (int t = 1; t <= n; ++t) {
int x1, x2, y1, y2, z1, z2; scanf("%d%d%d%d%d%d", &x1, &y1, &z1, &x2, &y2, &z2);
for (int i = x1+1; i <= x2; ++i) {
for (int j = y1+1; j <= y2; ++j)
for (int k = z1+1; k <= z2; ++k)
rec[i][j][k] = t;
}
}
for (int i = 1; i <= 100; ++i) {
for (int j = 1; j <= 100; ++j) {
for (int k = 1; k <= 100; ++k) {
if (!rec[i][j][k]) continue;
for (int t = 0; t < 6; ++t) {
int num = rec[i+dx[t]][j+dy[t]][k+dz[t]];
if (num && num != rec[i][j][k] && !st[make_pair(rec[i][j][k], num)])
ans[rec[i][j][k]] ++, st[make_pair(rec[i][j][k], num)] = 1;
}
}
}
}
for (int i = 1; i <= n; ++i) printf("%d\n", ans[i]);
return 0;
}
ABC312F. Cans and Openers:反悔贪心/二分(绿)
显然三项物品都是取 \(X_i\) 较大的更优,枚举取开罐器的数量,用一个大根堆维护普通罐头的价值,一个小根堆维护当前取的物品的最小值。每次取尽量多价值高的普通罐头替换掉价值低的易拉罐。注意判断边界。
时间复杂度 \(O(n\log n)\)。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <queue>
using namespace std;
typedef long long ll;
int n, m, cnt; ll ans;
priority_queue<int, vector<int>, greater<int>> use;
priority_queue<int, vector<int>> recan;
vector<int> can, opener;
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++i) {
int t, x; scanf("%d%d", &t, &x);
if (t == 0) can.push_back(x);
else if (t == 1) recan.push(x);
else opener.push_back(x);
}
sort(can.begin(), can.end(), greater<int>());
for (int i = 0; i < min(m, (int)can.size()); ++i) use.push(can[i]), ans += can[i], cnt ++;
sort(opener.begin(), opener.end(), greater<int>());
for (int i = 1; i <= min(m, (int)opener.size()); ++i) {
ll sum = ans;
if (cnt < m) cnt ++;
else if (use.size()) {int t = use.top(); use.pop(); sum -= t;}
else break;
int num = opener[i-1];
if (!recan.size()) break;
while (num && cnt < m && recan.size()) {
int x = recan.top();
num --, cnt ++, sum += x, use.push(x), recan.pop();
}
if (!use.size()) break;
while (num && recan.size() && use.size()) {
int x = recan.top(), y = use.top();
if (x > y) recan.pop(), use.pop(), num --, sum += x-y, use.push(x);
else break;
}
if (sum > ans) ans = sum; else break;
}
printf("%lld\n", ans);
return 0;
}
ABC312G. Avoid Straight Line:数学,dfs(绿)
正难则反,考虑不合法的 \((i,j,k)\) 三元组数量 \(ans\)。dfs 过程中枚举 \(j\),以 \(j\) 作为从 \(i\) 到 \(k\) 简单路径上的一点,则有两种情况:
- \(i,k\) 在 \(j\) 的不同子树内:\(sum\cdot siz_v\)。其中 \(sum\) 表示之前遍历过的 \(u\) 的子树大小之和。
- \(i\) 在 \(j\) 子树内,\(k\) 在 \(j\) 子树外:\((siz_j-1)(n-siz_j)\)。
则答案为 \(\dfrac{n(n-1)(n-2)}{6}-ans\)。
时间复杂度 \(O(n)\)。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <vector>
using namespace std;
typedef long long ll;
const int N = 2e5+10;
int n, siz[N]; vector<int> e[N];
ll ans;
void dfs(int u, int fa) {
int sum = 0; siz[u] = 1;
for (auto v : e[u]) {
if (v == fa) continue;
dfs(v, u); siz[u] += siz[v];
// i, k 均在 j 不同子树内
ans += (ll)siz[v] * sum, sum += siz[v];
}
// i 在子树内, j 在子树外
ans += (ll)(siz[u]-1) * (n-siz[u]);
}
int main() {
scanf("%d", &n);
for (int i = 1; i < n; ++i) {
int u, v; scanf("%d%d", &u, &v);
e[u].push_back(v), e[v].push_back(u);
}
dfs(1, 1);
printf("%lld\n", (ll)n*(n-1)*(n-2)/6-ans);
return 0;
}
ABC312Ex. snukesnuke:KMP(蓝)
对于每个字符串,通过 KMP 求出其循环节(若 \(n-ne_{siz}\) 能整除 \(siz\),则循环节长度为 \(n-ne_{siz}\),否则为 \(siz\))。将相同循环节的字符串放在一起,可以发现,不同循环节的字符串之间的答案是相互独立的。那么我们就将问题转变为:
- 给定 \(i\),求第一个未被使用过的 \(x\) 满足 \(x\) 为 \(i\) 的倍数。对应字符串的答案即为 \(\dfrac{x}{i}\)。
可以通过记录每一个循环节上一次使用的长度来计算,降低暴力的时间复杂度。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <unordered_map>
using namespace std;
const int N = 2e5+10;
int n, ne[N], ans[N]; char s[N];
int idx; unordered_map<string, int> S;
vector<pair<int, int>> sub[N];
int last[N]; bool st[N];
void kmp(int siz) {
ne[1] = 0;
for (int i = 2, j = 0; i <= siz; ++i) {
while (j && s[j+1] != s[i]) j = ne[j];
if (s[j+1] == s[i]) j ++;
ne[i] = j;
}
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n;
for (int i = 1; i <= n; ++i) {
cin >> s+1; int k = strlen(s+1); kmp(k);
string str; for (int j = 1; j <= ((k%(k-ne[k]))?k:(k-ne[k])); ++j) str += s[j];
if (!S[str]) S[str] = ++ idx;
sub[S[str]].push_back(make_pair(((k%(k-ne[k]))?k:k/(k-ne[k])), i));
}
for (int i = 1; i <= idx; ++i) {
memset(st, 0, sizeof st);
for (auto p : sub[i]) last[p.first] = p.first;
for (auto p : sub[i]) {
int cnt = p.first, id = p.second;
while (st[last[cnt]]) last[cnt] += cnt;
st[last[cnt]] = 1, ans[id] = last[cnt]/cnt;
}
}
for (int i = 1; i <= n; ++i) cout << ans[i] << ' ';
return 0;
}
7.31(Day 7)
P3398 仓鼠找 sugar:LCA(蓝)
此题有两个结论:
- 若树上两条路径 \(a\rightarrow b,c\rightarrow d\) 相交,则一定有 \(\text{lca}(a,b)\) 在路径 \(c\rightarrow d\) 上或 \(\text{lca}(c,d)\) 在路径 \(a\rightarrow b\) 上。
- 若 \(dist(u,x)+dist(x,v)=dist(u,v)\),则 \(x\) 在 \(u\rightarrow v\) 路径上。
做完了。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <vector>
#include <cmath>
using namespace std;
const int N = 1e5+10;
int n, m;
vector<int> e[N];
int dep[N], pos[N], idx, dfn[N<<1], f[N<<1][20];
void dfs(int u, int fa) {
dfn[++ idx] = u, pos[u] = idx, dep[u] = dep[fa]+1;
for (auto v : e[u]) {
if (v == fa) continue;
dfs(v, u), dfn[++ idx] = u;
}
}
int Min(int u, int v) {
return (pos[u] < pos[v]) ? u : v;
}
void init() {
for (int i = 1; i <= idx; ++i) f[i][0] = dfn[i];
for (int j = 1; 1<<j <= idx; ++j) {
for (int i = 1; i+(1<<j)-1 <= idx; ++i)
f[i][j] = Min(f[i][j-1], f[i+(1<<j-1)][j-1]);
}
}
int query(int l, int r) {
if (l > r) swap(l, r);
int k = log2(r-l+1);
return Min(f[l][k], f[r-(1<<k)+1][k]);
}
int lca(int u, int v) {
return query(pos[u], pos[v]);
}
int dist(int u, int v) {
return dep[u] + dep[v] - 2 * dep[lca(u, v)];
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i < n; ++i) {
int u, v; scanf("%d%d", &u, &v);
e[u].push_back(v), e[v].push_back(u);
}
dfs(1, 1), init();
while (m -- ) {
int a, b, c, d; scanf("%d%d%d%d", &a, &b, &c, &d);
int f1 = lca(a, b), f2 = lca(c, d);
if ((dist(a, b) == dist(a, f2)+dist(f2, b)) || dist(c, d) == dist(c, f1)+dist(f1, d)) puts("Y");
else puts("N");
}
return 0;
}
P1967 [NOIP2013 提高组] 货车运输:生成树(Kruscal),倍增,LCA(蓝)
我们跑一遍 Kruscal 求出每一个连通块的最大生成树,使得同一个连通块内两点之间的最小距离尽可能大,那么只需要在每一棵最大生成树内倍增求出答案即可。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <vector>
using namespace std;
typedef pair<int, int> pii;
const int N = 1e4+10;
int n, m, q;
vector<pii> e[N]; // 最大生成树
int p[N];
struct Edge {
int u, v, w;
bool operator > (const Edge &T) const {
return w > T.w;
}
};
vector<Edge> E;
int find(int x) {
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
void kruscal() {
sort(E.begin(), E.end(), greater<Edge>());
for (auto edg : E) {
int u = edg.u, v = edg.v, w = edg.w, fu = find(u), fv = find(v);
if (fu != fv) p[fu] = fv; else continue;
e[u].push_back(make_pair(v, w)), e[v].push_back(make_pair(u, w));
}
}
int f[N][20] /*树上2^k级祖先*/, g[N][20] /*跳2^k条边最小值*/, dep[N];
bool st[N];
void dfs(int u, int fa) {
st[u] = 1; dep[u] = dep[fa]+1;
for (auto edg : e[u]) {
int v = edg.first, w = edg.second;
if (st[v]) continue;
f[v][0] = u, g[v][0] = w;
for (int j = 1; 1<<j <= n; ++j) {
int t = f[v][j-1];
f[v][j] = f[t][j-1], g[v][j] = min(g[v][j-1], g[t][j-1]);
}
dfs(v, u);
}
}
int solve(int u, int v) {
int k = 18, t = 18, ans = 1e9;
if (dep[u] < dep[v]) swap(u, v);
while (t >= 0) {
if (dep[f[u][t]] >= dep[v]) ans = min(ans, g[u][t]), u = f[u][t];
t --;
}
if (u == v) return ans;
while (k >= 0) {
if (f[u][k] != f[v][k]) {
ans = min(ans, min(g[u][k], g[v][k]));
u = f[u][k], v = f[v][k];
}
k --;
}
ans = min(ans, min(g[u][0], g[v][0]));
return ans;
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++i) p[i] = i;
for (int i = 1; i <= m; ++i) {
int u, v, w; scanf("%d%d%d", &u, &v, &w);
Edge edg = {u, v, w};
E.push_back(edg);
}
kruscal();
for (int i = 1; i <= n; ++i) {
if (!st[i]) {
for (int j = 0; 1<<j <= n; ++j) g[i][j] = (int)1e9;
dfs(i, i);
}
}
scanf("%d", &q);
while (q -- ) {
int u, v; scanf("%d%d", &u, &v);
int fu = find(u), fv = find(v);
if (fu != fv) {puts("-1"); continue;}
printf("%d\n", solve(u, v));
}
return 0;
}
P1637 三元上升子序列:树状数组(绿)
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
typedef long long ll;
const int N = 3e4+10, M = 1e5+10;
int n, m, a[N], count[N];
int c[M]; ll ans;
int lowbit(int x) {
return x & -x;
}
void add(int x, int k) {
for (int i = x; i <= 1e5; i += lowbit(i))
c[i] += k;
}
int query(int x) {
int sum = 0;
for (int i = x; i > 0; i -= lowbit(i))
sum += c[i];
return sum;
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) {
scanf("%d", &a[i]); count[i] = query(a[i]-1);
add(a[i], 1);
}
memset(c, 0, sizeof c);
for (int i = n; i >= 1; --i) {
ans += (ll)count[i] * (query(1e5)-query(a[i]));
add(a[i], 1);
}
printf("%lld\n", ans);
return 0;
}
8.4
SP14138. AFS - Amazing Factor Sequence:数学,约数,前缀和(黄)
题目所求应为:
其中 \(\sigma (i)\) 表示 \(i\) 的所有约数之和。
筛一遍即可。时间复杂度 \(O(n\log n)\)。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
#define int long long
const int N = 1e6+10;
int t, n, d[N];
signed main() {
for (int i = 1; i <= 1000000; ++i) {
for (int j = i+i; j <= 1000000; j += i)
d[j] += i;
}
for (int i = 1; i <= 1000000; ++i) d[i] += d[i-1];
scanf("%lld", &t);
while (t -- ) scanf("%lld", &n), printf("%lld\n", d[n]);
return 0;
}
SP14168. AFS2 - Amazing Factor Sequence (medium):数学,约数,数论分块(蓝)
推一下式子:
这是整除分块的经典形式,可以在 \(O(T\sqrt n)\) 内解决。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long ll;
#define int __int128
ll t, n;
void write(int x){
char ch[40];
int len = 0;
if(x < 0)
putchar('-'), x = -x;
do {
ch[len++] = (x%10)^48;
x /= 10;
}
while(x);
while(len--)
putchar(ch[len]);
putchar('\n');
}
int calc(int l, int r) {
return r*(r+1)/2 - l*(l-1)/2;
}
int solve(int n) {
int l = 0, r = 0, ans = 0;
while (l <= n) {
l = r + 1;
if (n / l == 0) break;
r = min(n/(n/l), n);
ans += calc(l, r) * (n/l);
}
ans -= n*(n+1) / 2;
return ans;
}
signed main() {
scanf("%lld", &t);
while (t -- ) scanf("%lld", &n), write(solve(n));
return 0;
}
ABC 补题(8.5-8.10)
ABC 313
ABC313A. To Be Saikyo:枚举(红)
点击查看代码
#include <iostream>
#include <cstdio>
using namespace std;
const int N = 110;
int n, ans, p[N];
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%d", &p[i]);
for (int i = 2; i <= n; ++i) ans = max(ans, p[i]-p[1]+1);
printf("%d\n", ans);
}
ABC313B. Who is Saikyo:dfs(橙)
点击查看代码
#include <iostream>
#include <cstdio>
#include <vector>
using namespace std;
int n, m, deg[55]; vector<int> e[55];
bool st[55];
void dfs(int u) {
st[u] = 1;
for (auto v : e[u]) {
if (!st[v])
dfs(v);
}
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= m; ++i) {
int u, v; scanf("%d%d", &u, &v);
e[u].push_back(v), deg[v] ++;
}
for (int i = 1; i <= n; ++i) {
if (!deg[i]) {
dfs(i);
for (int j = 1; j <= n; ++j) {
if (!st[j])
puts("-1"), exit(0);
}
printf("%d\n", i);
break;
}
}
}
ABC313C. Approximate Equalization 2:数学,枚举(黄)
一次操作后和不变,想到让它们都接近平均数,然后人类智慧。(官方题解)
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
#define int long long
const int N = 2e5+10;
int n, sum, d1, d2, cnt1, cnt2, a[N];
signed main() {
scanf("%lld", &n);
for (int i = 1; i <= n; ++i) scanf("%lld", &a[i]), sum += a[i];
d1 = sum / n, d2 = d1 + 1;
for (int i = 1; i <= n; ++i) {
if (a[i] <= d1) cnt1 += d1-a[i];
else cnt2 += a[i]-d2;
}
if (cnt1 < cnt2) swap(cnt1, cnt2);
while (cnt2 < cnt1) cnt2 ++;
printf("%lld\n", (cnt1+cnt2)/2);
}
ABC313D. Odd or Even:数学,交互题(绿)
令 \(num_i\) 表示 \(i\sim i+k-1\) 这 \(k\) 个数的查询结果,\(s_i\) 表示 \(1,2,\cdots,i-1,i+1,\cdots, k+1\;(2\le i\le k)\) 这 \(k\) 个数的查询结果。令 \(c_i=(a_i+a_{k+1})\bmod 2\;(1\le i\le k)\),则 \(c_1=(num_1+num_2)\bmod 2\),\(c_i=(num_1+s_i)\bmod 2\;(2\le i\le k)\)。那么有:
由于 \(k\) 为奇数,所以 \(k\cdot a_{k+1}\) 与 \(a_{k+1}\) 同奇偶。令 \(cnt=\sum_{i=1}^n c_i\bmod 2\),则 \(cnt=num_1\) 时 \(a_{k+1}=0\),否则 \(a_{k+1}=1\)。这样就可以根据 \(c_i\) 再推出前 \(k\) 个数的奇偶性。
对于后 \(n-k\) 个数,由于 \(a_i=(num_{i-k}+num_{i-k+1}+a_{i-k})\bmod 2\),也可以递推得到答案。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, k, ans[N], num[N], c[N];
int main() {
cin >> n >> k;
for (int i = 1; i <= n-k+1; ++i) {
cout << "? ";
for (int j = i; j <= i+k-1; ++j) cout << j << ' '; cout << endl;
cin >> num[i];
}
for (int i = 2; i <= k; ++i) {
cout << "? ";
for (int j = 1; j <= k+1; ++j) {
if (j == i) continue;
cout << j << ' ';
}
cout << endl;
cin >> c[i]; c[i] = c[i] + num[1] & 1;
}
c[1] = num[1]+num[2] & 1;
int cnt = 0;
for (int i = 1; i <= k; ++i) cnt = cnt+c[i] & 1;
ans[k+1] = (cnt == num[1]) ? 0 : 1;
for (int i = 1; i <= k; ++i) ans[i] = ans[k+1] + c[i] & 1;
for (int i = k+2; i <= n; ++i) ans[i] = num[i-k] + num[i-k+1] + ans[i-k] & 1;
cout << "! ";
for (int i = 1; i <= n; ++i) cout << ans[i] << ' '; cout << endl;
}
ABC313E. Duplicate:(*)递推(绿)
当 \(S_i>1,S_{i+1}>1\) 时,\(f(S)\) 可以无限延长下去。由此可以推得,合法的 \(S\) 一定是由单个 \(>1\) 的数字和仅由数字 \(0,1\) 组成的连续段依次拼接而成。
考虑倒推,假设考虑到 \(S_i\),当前答案为 \(ans\)。在 \(S_i\) 被删掉前,它一共复制了 \(ans\) 遍 \(S_i\) 个 \(S_{i-1}\),则 \(S_i\) 对答案的贡献为 \(ans\cdot S_i\)。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long ll;
const int N = 1e6+10, P = 998244353;
int n, ans, a[N];
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%1d", &a[i]);
for (int i = n; i >= 2; --i) {
if (a[i-1] > 1 && a[i] > 1) {ans = -1; break;}
ans = (ll)(ans+1) * a[i] % P;
}
printf("%d\n", ans);
return 0;
}
ABC313G. Redistribution of Piles:(*)类欧几里得算法/类欧(蓝)
题意:
给定一个由正整数构成的序列 \(a\) 和一个数 \(s=0\),有两种操作:
- A:全局非零数减 \(1\),\(s\) 加上减掉的数之和;
- B:若 \(s\ge n\),\(s\leftarrow (s-n)\),数列全局加 \(1\)。
求最终得到的序列数量模 \(998244353\) 的值。
首先我们注意到,在一次 B 操作后进行 A 操作是没有意义的。那么,最简的操作序列一定是 AA...ABB...B 的形式。可以证明,最简的操作序列与最终序列形成双射。
不妨先将序列 \(a\) 升序排列。假设我们执行 A 操作直到 \(a_{i-1}=0 \;(i>1)\),再进行 \(j\;(1\le j\le a_i-a_{i-1})\) 次 A 操作,则 \(s=\displaystyle \sum_{1\le k\le i-1}a_k+(n-i+1)(a_{i-1}+j)\)。由于我们最多可以进行 \(\left\lfloor\dfrac{s}{n}\right\rfloor\) 次 B 操作,则当前的贡献即为:
注意 \(a_1\) 需要单独计算,贡献为 \(a_1+1\)(可以进行 \(0\sim a_1\) 次 A 操作,注意到这时再做 B 操作是没有意义的)。
这样计算时间复杂度是 \(O(n\max\{A_i\})\) 的,显然超时。观察到后半部分是一个类欧的经典形式,可以递归计算。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
using namespace std;
#define int long long
const int N = 2e5+10, P = 998244353;
int n, ans, a[N], s[N];
int solve(int n, int a, int b, int c) {
int ac = a/c, bc = b/c, m = (a*n+b)/c;
if (!a) return (n+1)*bc % P;
if (a >= c || b >= c) return (n*(n+1)/2 * ac % P + (n+1)*bc % P + solve(n, a%c, b%c, c)) % P;
return (m*n%P - solve(m-1, c, c-b-1, a)%P + P) % P;
}
signed main() {
scanf("%lld", &n);
for (int i = 1; i <= n; ++i) scanf("%lld", &a[i]);
sort(a+1, a+n+1);
ans = a[1] + 1, s[1] = a[1];
for (int i = 2; i <= n; ++i)
s[i] = s[i-1]+a[i],
ans = (ans + solve(a[i]-a[i-1], n-i+1, (n-i+1)*a[i-1]+s[i-1], n)-solve(0, n-i+1, (n-i+1)*a[i-1]+s[i-1], n) + a[i]-a[i-1]) % P;
printf("%lld\n", (ans+P)%P);
return 0;
}
补充(类欧几里得算法):
可在 \(O(\log n)\) 时间复杂度内计算
设 \(f(n,a,b,c)=\sum_{i=0}^n\left \lfloor \dfrac{ai+b}{c} \right \rfloor\),先将 \(a,b\) 均化到小于 \(c\) 的形式:
考虑如何计算后半部分,令 $m=\left \lfloor \dfrac{an+b}{c} \right \rfloor $,我们有:
递归即可。
ABC 311
Toyota Programming Contest 2023#4(AtCoder Beginner Contest 311):solve 5/8, rk1481
ABC311A. First ABC:枚举,字符串(红)
点击查看代码
#include <iostream>
using namespace std;
int n, num[5]; char s[110];
int main() {
cin >> n >> s+1;
for (int i = 1; i <= n; ++i) {
num[s[i]-'A'] ++;
if (num[0] && num[1] && num[2]) {cout << i << '\n'; break;}
}
return 0;
}
ABC311B. Vacation Together:枚举(红)
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
int n, d, ans, cnt;
char s[110][110];
int main() {
cin >> n >> d;
for (int i = 1; i <= n; ++i) cin >> s[i]+1;
for (int i = 1; i <= d; ++i) {
bool check = 1;
for (int j = 1; j <= n; ++j) {
if (s[j][i] == 'x') {
check = 0;
break;
}
}
if (check) cnt ++;
ans = max(ans, cnt);
if (!check) cnt = 0;
}
printf("%d\n", ans);
return 0;
}
ABC311C. Find it!:dfs(黄)
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 2e5+10;
int n, a[N];
bool st[N];
vector<int> nums;
void dfs(int u) {
if (st[u]) {
for (int i = 0; i < nums.size(); ++i) {
if (nums[i] == u) {
printf("%d\n", nums.size()-i);
for (int j = i; j < nums.size(); ++j)
printf("%d ", nums[j]);
}
}
exit(0);
}
st[u] = 1;
nums.push_back(u);
dfs(a[u]);
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
for (int i = 1; i <= n; ++i) {
nums.clear();
dfs(i);
}
return 0;
}
ABC311D. Grid Ice Floor:dfs(黄)
注意要判断是否和上一次的方向相反, 不然会超时。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 210;
const int dx[] = {-1, 0, 1, 0}, dy[] = {0, -1, 0, 1};
int n, m, cnt;
bool use[N][N], st[N][N][4];
char s[N][N];
void dfs(int x, int y, int last) {
for (int i = 0; i < 4; ++i) {
int x_ = x+dx[i], y_ = y+dy[i];
if ((i == 0 && last == 2) || (i == 1 && last == 3)
|| (i == 2 && last == 0) || (i == 3 && last == 1)) continue;
while (s[x_][y_] == '.') {
if (!use[x_][y_]) cnt ++, use[x_][y_] = 1;
x_ += dx[i], y_ += dy[i];
}
x_ -= dx[i], y_ -= dy[i];
if (!st[x_][y_][i]) st[x_][y_][i] = 1, dfs(x_, y_, i);
}
return ;
}
int main() {
cin >> n >> m;
for (int i = 1; i <= n; ++i) cin >> s[i]+1;
use[2][2] = 1, cnt ++;
dfs(2, 2, -1);
cout << cnt << '\n';
return 0;
}
ABC311E. Defect-free Squares:二维前缀和,二分(黄)
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 3010;
typedef long long ll;
int h, w, n; ll ans;
int s[N][N];
int main() {
scanf("%d%d%d", &h, &w, &n);
for (int i = 1; i <= n; ++i) {
int x, y; scanf("%d%d", &x, &y);
s[x][y] ++;
}
for (int i = 1; i <= h; ++i) {
for (int j = 1; j <= w; ++j)
s[i][j] = s[i][j]+s[i-1][j]+s[i][j-1]-s[i-1][j-1];
}
for (int i = 1; i <= h; ++i) {
for (int j = 1; j <= w; ++j) {
if (s[i][j]-s[i-1][j]-s[i][j-1]+s[i-1][j-1] == 1) continue;
int l = 1, r = min(h-i+1, w-j+1);
while (l < r) {
int mid = l + r + 1 >> 1;
int x = i+mid-1, y = j+mid-1;
if (s[x][y]-s[i-1][y]-s[x][j-1]+s[i-1][j-1] >= 1) r = mid-1;
else l = mid;
}
ans += l;
}
}
printf("%lld\n", ans);
return 0;
}
ABC311F. Yet Another Grid Task:线性 dp(蓝)
令 \(h_i\) 表示第 \(i\) 列中最高的黑色格子所在的行数,则第 \(i\) 列中 \(h_i\) 行以下的位置必定全部涂黑。考虑第 \(i\) 列涂黑一些格子后新的最高行数 \(j\),显然有 \(h_{i-1}-1\le j\le n\)。
可以发现,每一列的情况数只与上一列的情况数相关。考虑 dp,令 \(f_{i,j}\) 表示第 \(i\) 列最高黑色格子行数为 \(j\) 时的情况数,则有:
这个式子显然可以前缀和优化,时间复杂度 \(O(n^2)\)。通过滚动数组,可以将空间复杂度降低至 \(O(n)\)。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 2010, P = 998244353;
int n, m, ans, h[N], f[N], s[N];
char c[N];
int main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m;
for (int i = n; i >= 1; --i) {
cin >> c+1;
for (int j = 1; j <= m; ++j) if (c[j] == '#' && !h[j]) h[j] = i;
}
f[0] = 1;
for (int i = 1; i <= m; ++i) {
s[0] = f[0];
for (int j = 1; j <= n; ++j) s[j] = (s[j-1] + f[j]) % P;
for (int j = 0; j < h[i]; ++j) f[j] = 0;
for (int j = h[i]; j <= n; ++j) f[j] = ((s[min(n, j+1)] - ((h[i-1]>0)?(s[h[i-1]-1]):0)) % P + P) % P;
}
for (int i = h[m]; i <= n; ++i) ans = (ans + f[i]) % P;
cout << ans << '\n';
return 0;
}
ABC311G. One More Grid Task:单调栈,st 表,枚举(蓝)
先考虑一维的情况。我们可以枚举每一个 \(a_i\) 作为最小值,找到第一个在 \(a_i\) 左边且小于 \(a_i\) 的数 \(a_{l}\),第一个在 \(a_i\) 右边且小于 \(a_i\) 的数 \(a_r\),\(l,r\) 都可以用单调栈计算。这样,答案即为 \(\displaystyle\max_{1\le i\le n}\left\{a_i\times \sum_{l<j< r}a_j\right\}\)。
当所求为二维时,我们可以枚举矩形的上下边界 \(L,R\),令 \(b_j=\displaystyle\min_{L\le i\le R} a_{i,j}\),就可以转化为一维的情况了。
时间复杂度 \(O(n^2m)\)。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <stack>
using namespace std;
typedef long long ll;
const int N = 310;
int n, m, a[N][N], sum[N][N], b[N];
int f[N][N][10], L[N], R[N];
ll ans;
int query(int x, int l, int r) {
int k = log2(r-l+1);
return min(f[x][l][k], f[x][r-(1<<k)+1][k]);
}
int getsum(int x1, int y1, int x2, int y2) {
return sum[x2][y2] - sum[x2][y1-1] - sum[x1-1][y2] + sum[x1-1][y1-1];
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= m; ++j)
scanf("%d", &a[i][j]), sum[i][j] = sum[i][j-1]+sum[i-1][j]-sum[i-1][j-1]+a[i][j];
}
for (int i = 1; i <= m; ++i) {
for (int j = 1; j <= n; ++j) f[i][j][0] = a[j][i];
for (int k = 1; (1<<k) <= n; ++k) {
for (int j = 1; j+(1<<k)-1 <= n; ++j)
f[i][j][k] = min(f[i][j][k-1], f[i][j+(1<<k-1)][k-1]);
}
}
for (int i = 1; i <= n; ++i) {
for (int j = i; j <= n; ++j) {
stack<int> s; // 单调栈
for (int k = 1; k <= m; ++k) b[k] = query(k, i, j);
for (int k = 1; k <= m; ++k) {
while (s.size() && b[s.top()] >= b[k]) s.pop();
L[k] = (s.size())?(s.top()+1):1, s.push(k);
}
while (s.size()) s.pop();
for (int k = m; k >= 1; --k) {
while (s.size() && b[s.top()] >= b[k]) s.pop();
R[k] = (s.size())?(s.top()-1):m, s.push(k);
}
for (int k = 1; k <= m; ++k) ans = max(ans, (ll)getsum(i, L[k], j, R[k])*b[k]);
}
}
printf("%lld\n", ans);
return 0;
}
ABC 310
ABC310D. Peaceful Teams:dfs(黄)
暴搜即可,注意需要剪枝。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
int n, t, m, group[15]; ll ans;
pii dif[65];
void dfs(int now, int team) {
if (now > n) {
if (team != t) return ;
for (int i = 1; i <= m; ++i) {
int a = dif[i].first, b = dif[i].second;
if (group[a] == group[b]) return ;
}
ans ++;
}
for (int i = 1; i <= team; ++i) if (n-now >= t-team) group[now] = i, dfs(now+1, team);
if (team+1 <= t) group[now] = team+1, dfs(now+1, team+1);
}
int main() {
scanf("%d%d%d", &n, &t, &m);
for (int i = 1; i <= m; ++i) scanf("%d%d", &dif[i].first, &dif[i].second);
dfs(1, 0);
printf("%lld\n", ans);
return 0;
}
ABC310E. NAND repeatedly:数学,位运算(绿)
考虑枚举 \(j\)。显然 \(A_j=0\) 时,\(\forall 1\le i<j,f(i,j)=1\)。那么 \(j\) 对答案的贡献为 \(j-1\)。
\(A_j=1\) 时,我们记上一个 \(0\) 出现的位置为 \(last\),则 \(A_j\) 前有 \(j-last\) 个连续的 \(1\)。
- \(last<i\le j\):显然奇数个 \(1\) 依次 NAND 的结果为 \(1\),偶数个 \(1\) 依次 NAND 的结果为 \(0\)。那么这些连续的 \(1\) 对答案的贡献为 \(\left\lceil \dfrac{j-last}{2} \right\rceil\)。
- \(i=last\):由于 \(0\overline{ \wedge }1=1\),所以此时 \(last\) 对答案的贡献取决于 \(j-last\) 是否为奇数,若为奇数则其对答案的贡献为 \(1\),否则为 \(0\)。
- \(1\le i<last\):此时 \(f(i,last)=1\),那么会产生 \(j-last+1\) 个连续的 \(1\),若其为奇数则其对答案的贡献为 \(last-1\),否则为 \(0\)。
将这三部分加起来即可。注意特判 \(last=0\) 即 \(0\) 还未出现的情况。
时间复杂度 \(O(n)\)。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long ll;
const int N = 1e6+10;
int n, last, a[N]; ll ans;
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%1d", &a[i]);
for (int i = 1; i <= n; ++i) {
if (!a[i]) ans += i-1, last = i;
else {
int len = i-last;
ans += (len+1)/2 + (last>0)*(len&1) + (last>0)*(len+1&1)*(last-1);
}
}
printf("%lld\n", ans);
return 0;
}
ABC310F. Make 10 Again:(*)数学,逆元,概率,状压 dp(蓝)
注意到我们只需要考虑骰子掷出的点数 \(\le 10\) 的情况。令 \(f_{i,S}\) 表示考虑到前 \(i\) 个骰子,其掷出的数组成 \(0\sim 10\) 之间的数的状态为 \(S\) 的概率。初始状态为:
接下来考虑状态转移。假设第 \(i\) 个骰子掷出的数为 \(x\),显然其概率为 \(\dfrac{1}{A_i}\)。对于前 \(i-1\) 个骰子掷出的数组成的状态 \(S'\),那么前 \(i\) 个骰子掷出的数组成的状态 \(S\) 一定包含 \(x\) 和 \(x+y\;(y\in S')\)。当 \(x\ge 10\) 时,第 \(i\) 个骰子无法对答案作出贡献,则 \(S=S'\),概率为 \(\dfrac{A_i-10}{A_i}\)。那么状态转移方程为:
答案显然为:
时间复杂度 \(O(nV2^V\log P)\)。其中 \(V\) 为值域。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long ll;
const int N = 110, p = 998244353;
int n, ans, a[N], f[N][5000];
int power(int a, int b) {
int res = 1;
while (b) {
if (b & 1) res = (ll)res * a % p;
a = (ll)a * a % p;
b >>= 1;
}
return res;
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
f[0][1] = 1;
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= min(a[i], 10); ++j) {
for (int s = 1; s <= (1<<11)-1; ++s) {
int S = s | ((s << j) & ((1<<11)-1));
f[i][S] = (f[i][S] + (ll)f[i-1][s] * power(a[i], p-2)) % p;
}
}
if (a[i] <= 10) continue;
for (int s = 1; s <= (1<<11)-1; ++s)
f[i][s] = (f[i][s] + (ll)f[i-1][s] * (a[i]-10) % p * power(a[i], p-2)) % p;
}
for (int s = 1; s <= (1<<11)-1; ++s) {
if ((s>>10) & 1)
ans = ((ll)ans + f[n][s]) % p;
}
printf("%d\n", ans);
return 0;
}
ABC310G. Takahashi And Pass-The-Ball Game:(*)倍增(蓝)
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <vector>
using namespace std;
#define int long long
const int P = 998244353;
int n, k, inv;
int power(int a, int b) {
int res = 1;
while (b) {
if (b & 1) res = res * a % P;
a = a * a % P;
b >>= 1;
}
return res;
}
void move(vector<int> &a, vector<int> &b) { // 进行一次倍增
vector<int> res(n+1);
for (int i = 1; i <= n; ++i) res[i] = a[b[i]];
a = res;
}
vector<int> modify(vector<int> a, vector<int> x) { // 进行一次转换
vector<int> now(n+1);
for (int i = 1; i <= n; ++i) now[a[i]] = (now[a[i]]+x[i]) % P;
return now;
}
void add(vector<int> &x, vector<int> y) {
for (int i = 1; i <= n; ++i) x[i] = (x[i]+y[i]) % P;
}
signed main() {
scanf("%lld%lld", &n, &k);
inv = power(k%P, P-2);
vector<int> a(n+1), b(n+1), ans(n+1);
for (int i = 1; i <= n; ++i) scanf("%lld", &a[i]);
for (int i = 1; i <= n; ++i) scanf("%lld", &b[i]);
b = modify(a, b);
while (k) {
if (k & 1) add(ans, b), b = modify(a, b);
// 类似快速幂, 只有在k当前位为1时累加答案
add(b, modify(a, b)); // 更新b数组,累加上2^{i-1}次的答案
move(a, a); // 相当于移动2^i次
k >>= 1;
}
for (int i = 1; i <= n; ++i) printf("%lld ", ans[i]*inv%P);
return 0;
}
ABC 309
ABC309D. Add One Edge:bfs(黄)
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 3e5+10;
int n1, n2, m, dis[N], ans;
vector<int> e[N];
void bfs(int s) {
queue<int> q; q.push(s), dis[s] = 1;
while (q.size()) {
int u = q.front(); q.pop();
for (auto v : e[u]) {
if (dis[v]) continue;
q.push(v), dis[v] = dis[u]+1;
}
}
}
int main() {
scanf("%d%d%d", &n1, &n2, &m);
while (m -- ) {
int u, v; scanf("%d%d", &u, &v);
e[u].push_back(v), e[v].push_back(u);
}
bfs(1), bfs(n1+n2);
int maxl = 0;
for (int i = 1; i <= n1; ++i) maxl = max(maxl, dis[i]-1);
for (int i = n1+1; i <= n1+n2; ++i) ans = max(ans, maxl+dis[i]);
printf("%d\n", ans);
return 0;
}
ABC309E. Family and Insurance:dfs(黄)
记录每个点能够到达的最大深度。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 3e5+10;
int n, m, ans, a[N]; bool check[N];
vector<int> e[N];
void dfs(int u, int dep) {
int d = max(dep, (a[u]>0)?(a[u]+1):0); check[u] = 1;
if (d) ans ++;
for (auto v : e[u]) dfs(v, max(d-1, 0));
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 2; i <= n; ++i) {
int p; scanf("%d", &p);
e[p].push_back(i);
}
while (m -- ) {
int x, y; scanf("%d%d", &x, &y);
a[x] = max(a[x], y);
}
for (int i = 1; i <= n; ++i) {
if (!check[i])
dfs(i, a[i]);
}
printf("%d\n", ans);
return 0;
}
8.12
ABC314A. 3.14:枚举,字符串(红)
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <queue>
#include <cmath>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
int n;
string s = "3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679";
int main() {
cin >> n;
for (int i = 0; i < n+2; ++i) cout << s[i]; cout << '\n';
return 0;
}
ABC314B. Roulette:模拟(橙)
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <queue>
#include <cmath>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
int n, x;
vector<int> nums[110];
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) {
int c, t; scanf("%d", &c);
for (int j = 1; j <= c; ++j) scanf("%d", &t), nums[i].push_back(t);
}
scanf("%d", &x);
vector<int> ans;
for (int i = 1; i <= n; ++i) {
for (auto j : nums[i])
if (j == x)
ans.push_back(i);
}
if (!ans.size()) puts("0\n"), exit(0);
sort(ans.begin(), ans.end(), [](int a, int b){return nums[a].size()<nums[b].size();});
int minl = nums[ans[0]].size();
vector<int> now;
for (auto i : ans) {
if (nums[i].size() == minl)
now.push_back(i);
}
printf("%d\n", now.size());
sort(now.begin(), now.end());
for (auto i : now) printf("%d ", i); puts("");
return 0;
}
ABC314C. Rotate Colored Subsequence:字符串,模拟(橙)
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <queue>
#include <cmath>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
const int N = 2e5+10;
int n, m, c[N];
char s[N];
vector<int> col[N];
int main() {
cin >> n >> m >> s+1;
for (int i = 1; i <= n; ++i) {
cin >> c[i];
col[c[i]].push_back(i);
}
for (int i = 1; i <= m; ++i) {
if (col[i].size() < 2) continue;
for (int j = col[i].size()-1; j >= 1; --j) swap(s[col[i][j]], s[col[i][j-1]]);
}
for (int i = 1; i <= n; ++i) cout << s[i]; cout << '\n';
return 0;
}
ABC314D. LOWER:字符串,模拟(黄)
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <queue>
#include <cmath>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
const int N = 5e5+10;
int check = -1, now = 0;
bool use[N];
vector<int> nums;
int n, q;
char s[N];
int main() {
cin >> n >> s+1 >> q;
for (int i = 1; i <= q; ++i) {
int op, pos; char x;
cin >> op >> pos >> x;
if (op == 1) s[pos] = x, nums.push_back(pos);
else if (op == 2) check = 1, now = nums.size();
else check = 0, now = nums.size();
}
for (int i = now; i < nums.size(); ++i) use[nums[i]] = 1;
for (int i = 1; i <= n; ++i) {
if (check == -1 || use[i]) cout << s[i];
else if (check) cout << (char)tolower(s[i]);
else cout << (char)toupper(s[i]);
}
cout << '\n';
return 0;
}
ABC314E. Roulettes:期望 dp,数学(蓝)
令 \(f_i\) 表示已经取了 \(\ge i\) 时的最小期望步数,转移是显然的。难点在于如何处理 \(0\) 的情况。对于一个转盘,若其中非 \(0\) 数的数量为 \(x\),总数量为 \(y\),则 \(cost_i\leftarrow cost_i\times \dfrac{y}{x}\)。
记忆化搜索实现,时间复杂度 \(O(n^2m)\)。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <queue>
#include <cmath>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
const int N = 110;
int n, m;
double f[N]; // f[i]表示差为i的期望最小价值
vector<int> nums[N], cost, siz;
double dfs(int sum) {
if (sum <= 0) return 0;
if (f[sum]) return f[sum];
f[sum] = 1e9;
for (int i = 1; i <= n; ++i) {
double now = (double)cost[i-1] * siz[i-1] / nums[i].size();
// 选第i个转盘的期望价值
for (auto j : nums[i]) now += 1.0 / nums[i].size() * dfs(sum-j);
f[sum] = min(f[sum], now);
}
return f[sum];
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++i) {
int c, p, x; scanf("%d%d", &c, &p); cost.push_back(c), siz.push_back(p);
for (int j = 1; j <= p; ++j) {
scanf("%d", &x);
if (x) nums[i].push_back(x);
}
}
double ans = dfs(m);
printf("%.8f\n", ans);
return 0;
}
ABC314F. A Certain Game:期望,数学,并查集,dfs(蓝)
通过并查集合并两个集合,将合并后的集合作为一个点,向合并前的两个集合分别连一条边,显然最后会构成一棵树。从根节点出发遍历,\(ans_v=ans_u+w(u,v)\)。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <queue>
#include <cmath>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
const int N = 2e5+10, P = 998244353;
int n, idx, p[N], siz[N], dot[N], ans[N<<1];
vector<pii> e[N<<1];
int power(int a) {
int res = 1, b = P-2;
while (b) {
if (b & 1) res = (ll)res * a % P;
a = (ll)a * a % P;
b >>= 1;
}
return res;
}
void dfs(int u) {
for (auto edge : e[u]) {
int v = edge.first, w = edge.second;
ans[v] = ((ll)ans[u]+w) % P;
dfs(v);
}
}
int find(int x) {
return p[x] = (p[x] == x) ? x : find(p[x]);
}
int main() {
scanf("%d", &n); idx = n;
for (int i = 1; i <= n; ++i) p[i] = i, siz[i] = 1, dot[i] = i;
for (int i = 1; i < n; ++i) {
int u, v; scanf("%d%d", &u, &v); u = find(u), v = find(v);
int ne = ++ idx, inv = power(siz[u]+siz[v]);
e[ne].push_back({dot[u], (ll)siz[u]*inv%P}), e[ne].push_back({dot[v], (ll)siz[v]*inv%P});
p[u] = v, siz[v] += siz[u], dot[v] = ne;
}
dfs(idx);
for (int i = 1; i <= n; ++i) printf("%d ", ans[i]);
return 0;
}
8.15
P5124 [USACO18DEC] Teamwork G:dp,st 表(蓝)
令 \(f_i\) 表示前 \(i\) 头牛能力值之和的最大值,显然状态转移方程为:
st 表预处理区间最大值即可。
时间复杂度 \(O(nk)\)。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
using namespace std;
const int N = 1e4+10;
int n, k, a[N], st[N][25], f[N];
int query(int l, int r) {
int k = log2(r-l+1);
return max(st[l][k], st[r-(1<<k)+1][k]);
}
int main() {
scanf("%d%d", &n, &k);
for (int i = 1; i <= n; ++i) scanf("%d", &a[i]), st[i][0] = a[i];
for (int j = 1; (1<<j) <= n; ++j) {
for (int i = 1; i+(1<<j)-1 <= n; ++i)
st[i][j] = max(st[i][j-1], st[i+(1<<j-1)][j-1]);
}
for (int i = 1; i <= n; ++i) {
for (int j = max(i-k+1, 1); j <= i; ++j)
f[i] = max(f[i], f[j-1]+(i-j+1)*query(j, i));
}
return printf("%d\n", f[n]), 0;
}
P5017 [NOIP2018 普及组] 摆渡车:斜率优化 dp(蓝)
令 \(f_i\) 表示摆渡车从 \(i\) 时刻出发,所有到达时间 \(\le i\) 的人等待时间之和的最小值。显然状态转移方程为:
其中,\(s_i=\sum a_i,ss_i=\sum ia_i\)。
假设 \(f_i\) 可由 \(f_j\) 转移而来,可得斜截式:
单调性显然。
维护一个下凸壳即可。时间复杂度 \(O(t)\)。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <deque>
using namespace std;
#define int long long
const int M = 3.3e7;
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,M,stdin),p1==p2)?EOF:*p1++)
char buf[M],*p1=buf,*p2=buf;
template <typename T>
void read(T &x) {
x = 0;
register int flag = 1;
static char c = getchar();
while (!isdigit(c)) {
if (c == '-') flag = -1;
c = getchar();
}
while (isdigit(c)) {
x = x * 10 + c - '0';
c = getchar();
}
x *= flag;
}
const int N = 8e6+10;
int n, m, last, ans = 1e18, a[N], s[N], ss[N], f[N];
deque<int> q;
int getx(int j) {
return s[j];
}
int gety(int j) {
return f[j] + ss[j];
}
signed main() {
read(n), read(m);
for (int i = 1; i <= n; ++i) {
int t; read(t);
a[t] ++, last = max(last, t);
}
for (int i = 0; i <= last+m; ++i) s[i] = s[i-1] + a[i], ss[i] = ss[i-1] + i*a[i];
q.push_back(0);
for (int i = 0; i < m; ++i) f[i] = i*s[i] - ss[i];
for (int i = m; i <= last+m; ++i) {
int k = i;
while (q.size() > 1 && k*(getx(q[1])-getx(q[0])) >= gety(q[1])-gety(q[0])) q.pop_front();
int j = q[0], t = q.size()-1; f[i] = f[j] + i*(s[i]-s[j]) - (ss[i]-ss[j]);
while (q.size() > 1 && (gety(q[t])-gety(q[t-1]))*(getx(i-m+1)-getx(q[t])) >= (gety(i-m+1)-gety(q[t]))*(getx(q[t])-getx(q[t-1]))) q.pop_back(), t --;
q.push_back(i-m+1);
if (i >= last) ans = min(ans, f[i]);
}
return printf("%lld\n", ans), 0;
}
P4782 【模板】2-SAT 问题:2-sat(tarjan)(紫)
对于一个限制条件 \(x\wedge y\),我们可以将其理解为 \((\neg x\vee y)\wedge(x\vee \neg y)\)。那么我们可以从 \(\neg x\) 向 \(y\) 连一条有向边,\(\neg y\) 向 \(x\) 连一条有向边,即若 \(\neg x\) 一定有 \(y\),若 \(\neg y\) 一定有 \(x\)。
对于一个变量,我们分四种情况:
- \(x\) 可达 \(\neg x\),\(\neg x\) 可达 \(x\):无解;
- \(x\) 可达 \(\neg x\),\(\neg x\) 不可达 \(x\):\(x=0\);
- \(x\) 不可达 \(\neg x\),\(\neg x\) 可达 \(x\):\(x=1\);
- \(x\) 不可达 \(\neg x\),\(\neg x\) 不可达 \(x\):\(x=0/1\)。
我们通过 Tarjan 缩点时,其实就相当于求出了逆拓扑序。若 \(cnt_{x}<cnt_{\neg x}\),说明拓扑序中 \(x\) 所在的强连通分量在 \(\neg x\) 所在的强连通分量后面,即 \(\neg x\) 可能到达 \(x\),此时需要令 \(x=1\);反之即可令 \(x=0\)。
时间复杂度 \(O(n+m)\)。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <vector>
using namespace std;
#define rev(x) (x<=n)?(x+n):(x-n)
const int N = 2e6+10;
int n, m, num, top, cnt;
int dfn[N], low[N], stk[N], ins[N], c[N];
vector<int> e[N];
void tarjan(int u) {
dfn[u] = low[u] = ++ num, ins[u] = 1, stk[++ top] = u;
for (auto v : e[u]) {
if (!dfn[v]) tarjan(v), low[u] = min(low[u], low[v]);
else if (ins[v]) low[u] = min(low[u], dfn[v]);
}
if (low[u] == dfn[u]) {
int t = 0; cnt ++;
while (t != u) t = stk[top --], ins[t] = 0, c[t] = cnt;
}
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= m; ++i) {
int x, a, y, b; scanf("%d%d%d%d", &x, &a, &y, &b);
x = x+((!a)?n:0), y = y+((!b)?n:0);
e[rev(x)].push_back(y), e[rev(y)].push_back(x);
}
for (int i = 1; i <= n*2; ++i) if (!dfn[i]) tarjan(i);
for (int i = 1; i <= n; ++i) {
if (c[i] == c[n+i])
return puts("IMPOSSIBLE"), 0;
}
puts("POSSIBLE");
for (int i = 1; i <= n; ++i) printf("%d ", (c[i]<c[n+i]));
return 0;
}
P6348 [PA2011] Journeys:线段树,最短路,建图优化(紫)
用两个线段树分别表示每个区间连出去的边和连到每个区间的边,分别记作出树和入树。对于出树,子节点向父节点连一条长度为 \(0\) 的边,表示从子节点代表的区间可以走到父节点代表的区间;对于入树,父节点向子节点连一条长度为 \(0\) 的边,表示从父节点代表的区间可以走到子节点代表的区间。还需要从入树最底层的 \(n\) 个点连到出树最底层的 \(n\) 个点,边权为 \(0\)。
在本题中,我们需要从一个区间向另一个区间连边。那么我们需要将出树中的区间向一个虚点连一条边权为 \(1\) 的边,再将这个虚点向入树中的区间连一条边权为 \(0\) 的边。注意到本题中是双向边,需要执行两次。
时间复杂度 \(O(n\log n)\)。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <vector>
#include <deque>
#include <cstring>
using namespace std;
const int N = 3e6+10;
typedef pair<int, int> pii;
#define mpr(a,b) make_pair(a, b)
#define lson u<<1, l, mid
#define rson u<<1|1, mid+1, r
int n, m, p, idx;
int dist[N], ind[N], otd[N], to[N];
vector<pii> e[N];
void add(int u, int v, int w) {
e[u].push_back(mpr(v, w));
}
void build(int u, int l, int r) {
ind[u] = ++ idx, otd[u] = ++ idx;
if (l == r) {
add(ind[u], otd[u], 0); to[l] = ind[u];
if (l == p) add(0, ind[u], 0);
return ;
}
int mid = l + r >> 1;
build(lson), build(rson);
add(otd[u<<1], otd[u], 0), add(otd[u<<1|1], otd[u], 0);
add(ind[u], ind[u<<1], 0), add(ind[u], ind[u<<1|1], 0);
}
void modify(int u, int l, int r, int a, int b, int pos, int op) { // 0: 入树, 1: 出树
if (l >= a && r <= b) return (void)(op?add(otd[u], pos, 1):add(pos, ind[u], 0));
int mid = l + r >> 1;
if (a <= mid) modify(lson, a, b, pos, op);
if (b > mid) modify(rson, a, b, pos, op);
}
void bfs() {
memset(dist, 0x3f, sizeof dist);
deque<int> q; q.push_front(0), dist[0] = 0;
while (q.size()) {
int u = q.front(); q.pop_front();
for (auto edge : e[u]) {
int v = edge.first, w = edge.second;
if (dist[v] > dist[u]+w) {
dist[v] = dist[u]+w;
if (w == 1) q.push_back(v);
else q.push_front(v);
}
}
}
}
int main() {
scanf("%d%d%d", &n, &m, &p);
build(1, 1, n);
while (m -- ) {
int now = ++ idx;
int a, b, c, d; scanf("%d%d%d%d", &a, &b, &c, &d);
modify(1, 1, n, a, b, now, 1), modify(1, 1, n, c, d, now, 0);
now = ++ idx;
modify(1, 1, n, c, d, now, 1), modify(1, 1, n, a, b, now, 0);
}
bfs();
for (int i = 1; i <= n; ++i) printf("%d\n", dist[to[i]]);
return 0;
}
8.16
P4092 [HEOI2016/TJOI2016] 树:并查集,线段树(蓝)
倒序并查集即可。时间复杂度 \(O(n\log n)\)。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <queue>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
#define mpr(a,b) make_pair(a,b)
const int N = 1e5+10;
int n, q, fa[N], p[N], cnt[N], ans[N];
pii oper[N];
int find(int x) {
return (p[x] == x) ? p[x] : (p[x]=find(p[x]));
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> q; p[1] = 1;
for (int i = 1; i < n; ++i) {
int u, v; cin >> u >> v;
fa[v] = u, p[v] = u;
}
cnt[1] ++;
char op; int x;
for (int i = 1; i <= q; ++i) {
cin >> op >> x;
if (op == 'C') oper[i] = {0, x}, cnt[x] ++, p[x] = x;
else oper[i] = {1, x};
}
for (int i = q; i >= 1; --i) {
int op = oper[i].first, x = oper[i].second;
if (!op) {cnt[x] --; if (!cnt[x]) p[x] = fa[x];}
else ans[i] = find(x);
}
for (int i = 1; i <= q; ++i) if (ans[i]) cout << ans[i] << '\n';
return 0;
}
P2449 [SDOI2005] 矩形:模拟,并查集(黄)
并查集维护一块内的矩形即可。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <queue>
using namespace std;
const int N = 7010;
int n, p[N];
struct Rec {
int x1, y1, x2, y2;
} rec[N];
int find(int x) {
return (p[x] == x) ? p[x] : (p[x]=find(p[x]));
}
bool check(Rec A, Rec B) {
if ((A.x2<B.x1||B.x2<A.x1)||(A.y2<B.y1||B.y2<A.y1)) return 0; // 两个矩形无交
if ((A.x1==B.x2||A.x2==B.x1)&&(A.y1==B.y2||A.y2==B.y1)) return 0; // 两个矩形只有顶点相交
return 1; // 重复点>1
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) p[i] = i, scanf("%d%d%d%d", &rec[i].x1, &rec[i].y1, &rec[i].x2, &rec[i].y2);
for (int i = 1; i <= n; ++i)
for (int j = 1; j < i; ++j)
if (check(rec[i], rec[j]) && find(i) != find(j))
p[find(i)] = find(j);
int res = 0;
for (int i = 1; i <= n; ++i) if (p[i] == i) res ++;
printf("%d\n", res);
return 0;
}
CF1730D. Prefixes and Suffixes:思维,构造(蓝)
直接考虑 \(T\) 的后缀有点困难,考虑先将 \(T\) 翻转一下,记为 \(T'\)。则对于题目中的一次操作,相当于我们先将 \(S[1\sim k],T'[1\sim k]\) 翻转,然后再交换 \(S[1\sim k],T'[1\sim k]\)。那么可以发现,\(S_i\) 和 \(T'_i\) 的相对位置是不会改变的。那么我们可以用 \(P_i=(S_i,T_i')\) 表示 \(S,T'\) 中第 \(i\) 个位置上的字符对。
接下来,我们需要证明 \(2\) 个重要结论:
- \((S_i,T_i')\) 是可以任意排列的。
证明:
令当前序列为 \((S_1,T'_1),(S_2,T'_2),\cdots(S_n,T_n')\)。
假设我们已经排列好了第 \(j\) 位之后所有的元素,对于 \(1\le i\le j\),可以通过 \(2\) 次操作将 \((S_i,T_i')\) 移动至第 \(j\) 位 。
- \(k=i\):将 \((S_i,T_i')\) 移动至第 \(1\) 位,并交换为 \((T_i',S_i)\);
- \(k=j\):将 \((S_i,T_i')\) 移动至第 \(j\) 位,并交换为 \((S_i,T_i')\)。
这样我们就成功将 \((S_i,T_i')\) 移动至第 \(j\) 位 。
- \((S_i,T_i')\) 可以交换为 \((T_i',S_i)\) 。
证明:
- \(k=i\):将 \((S_i,T_i')\) 移动至第 \(1\) 位,并交换为 \((T_i',S_i)\);
- \(k=1\):将 \((S_i,T_i')\) 移动至第 \(1\) 位,并交换为 \((S_i,T_i')\);
- \(k=i\) :将 \((S_i,T_i')\) 移动至第 \(i\) 位,并交换为 \((T_i',S_i)\)。
这样我们就成功让 \((S_i,T_i')\) 交换为 \((T_i',S_i)\)。
到这一步就比较简单了。可以发现,对于最终的序列,一定有 \(S_i=T'_{n-i+1},T'_i=S_{n-i+1}\)。也就是说,如果我们不考虑一个对中的顺序,一定有 \(P_i=P_{n-i+1}\)。由此可以得到结论:
- \(n\) 为偶数时,每种对都需要出现偶数次。
- \(n\) 为奇数时,只有一种对 \((x,x)\) 可以出现奇数次,其余种类的对都需要出现偶数次。
通过哈希和桶实现,时间复杂度 \(O(T|\Sigma|^2)\)(\(|\Sigma|\) 为字符集大小)。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
typedef pair<int, int> pii;
#define Yes cout << "YES\n"
#define No cout << "NO\n"
const int N = 1e5+10;
int t, n, num[1000];
char S[N], T[N];
int h(int a, int b) {
if (a > b) swap(a, b);
return a*26 + b;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> t;
while (t -- ) {
memset(num, 0, sizeof num);
cin >> n >> S+1 >> T+1;
reverse(T+1, T+n+1);
for (int i = 1; i <= n; ++i) num[h(S[i]-'a', T[i]-'a')] ++;
int mid = -1;
for (int i = 0; i < 700; ++i) {
if (num[i] % 2) {
if (mid != -1) {mid = 1000; break;}
mid = i;
}
}
if (mid == 1000) No;
else if (n % 2) (mid/26 == mid%26) ? Yes : No;
else (mid != -1) ? No : Yes;
}
return 0;
}
8.17
CF597C. Subsequences:dp,树状数组(蓝)
令 \(f_{i,j}\) 表示长度为 \(i\),以 \(a_j\) 为结尾的上升子序列数量,那么状态转移方程为:
由于 \(a_k<a_j\),我们可以用树状数组优化转移。时间复杂度 \(O(nk\log n)\)。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
#define int long long
const int N = 1e5+10;
int n, k, a[N], c[N], f[15][N];
int lowbit(int x) {
return x & -x;
}
void add(int x, int k) {
for (int i = x; i <= n; i += lowbit(i))
c[i] += k;
}
int query(int x) {
int res = 0;
for (int i = x; i >= 1; i -= lowbit(i))
res += c[i];
return res;
}
signed main() {
scanf("%lld%lld", &n, &k);
for (int i = 1; i <= n; ++i) scanf("%lld", &a[i]);
for (int i = 1; i <= n; ++i) f[1][i] = 1;
for (int i = 2; i <= k+1; ++i) {
memset(c, 0, sizeof c);
for (int j = 1; j <= n; ++j) {
f[i][j] = query(a[j]);
add(a[j], f[i-1][j]);
}
}
int ans = 0; for (int i = 1; i <= n; ++i) ans += f[k+1][i]; printf("%lld\n", ans);
return 0;
}
P2054 [AHOI2005] 洗牌:数学,逆元,exgcd(蓝)
容易发现,第 \(i\) 张牌经过一次洗牌后会变为 \(2i\bmod (n+1)\)。那么我们需要求一个 \(x\) 满足 \(2^mx\equiv l\pmod {n+1}\),即 \(2^mx+(n+1)y=l\),可以用 exgcd 求解(\(n\) 为偶数,\(2^m\) 与 \(n+1\) 互质,必定有解)。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#define int long long
using namespace std;
int n, m, l;
int power(int a, int b, int p) {
int res = 1;
while (b) {
if (b & 1) res = (__int128)res * a % p;
a = (__int128)a * a % p;
b >>= 1;
}
return res;
}
int exgcd(int a, int b, int &x, int &y) {
if (!b) {return x = 1, y = 0, a;}
int d = exgcd(b, a%b, x, y); int t = y;
y = x - y*(a/b), x = t;
return d;
}
signed main() {
cin >> n >> m >> l;
int x, y, d = exgcd(power(2, m, n+1), n+1, x, y);
cout << (int)((__int128)l*x % (n+1) + n+1) % (n+1) << '\n';
return 0;
}
8.18
P3382 【模板】三分法:三分(黄)
取 \(lmid,rmid\) 分别为区间三等分点,若 \(f(lmid)<f(rmid)\) 则令 \(l=lmid\),否则令 \(r=rmid\)。
证明:
若 \(f(lmid)<f(rmid)\),此时最大值一定在 \(lmid\) 右侧。假设最大值 \(x\) 在 \(lmid\) 左侧,一定有 \(x>f(lmid)>f(rmid)\),矛盾。
若 \(f(lmid)>f(rmid)\),此时最大值一定在 \(rmid\) 左侧。证明同上。
时间复杂度 \(O(\log len)\)。略慢于二分。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <iomanip>
using namespace std;
const double eps = 1e-6;
int n; double l, r, f[20];
double calc(double x) {
double res = 0;
for (int i = 0; i <= n; ++i) res += pow(x, i) * f[i];
return res;
}
int main() {
cin >> n >> l >> r;
for (int i = n; i >= 0; --i) cin >> f[i];
while (r-l >= eps) {
double lmid = l + (r-l)/3.0, rmid = r - (r-l)/3.0;
if (calc(lmid) < calc(rmid)) l = lmid;
else r = rmid;
}
cout << fixed << setprecision(6) << l << '\n';
return 0;
}
P3381 【模板】最小费用最大流:费用流(蓝)
把 EK 算法求增广路的 bfs 换为 spfa 即可。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <queue>
using namespace std;
typedef long long ll;
const int N = 10010, M = 1e5+10;
const ll inf = 1e18;
int n, m, s, t; ll maxflow, mincost;
int idx = 1, e[M], h[N], ne[M]; ll flow[M], cost[M];
int pre[N]; ll dist[M], f[M]; bool check[N];
void add(int u, int v, int c, int w) {
e[++ idx] = v, ne[idx] = h[u], flow[idx] = c, cost[idx] = w, h[u] = idx;
}
bool spfa() {
memset(f, 0x7f, sizeof f), memset(dist, 0x7f, sizeof dist), memset(check, 0, sizeof check), memset(pre, 0, sizeof pre);
check[s] = 1, dist[s] = 0, f[s] = inf;
queue<int> q; q.push(s);
while (q.size()) {
int u = q.front(); q.pop();
check[u] = 0;
for (int i = h[u]; i != -1; i = ne[i]) {
int v = e[i];
if (flow[i] > 0 && dist[v]>dist[u]+cost[i]) {
dist[v] = dist[u] + cost[i], pre[v] = i, f[v] = min(f[u], flow[i]);
if (!check[v]) check[v] = 1, q.push(v);
}
}
}
return (dist[t] < inf);
}
void MCMF() {
while (spfa()) {
int v = t;
maxflow += f[t], mincost += dist[t]*f[t];
while (v != s) {
int i = pre[v];
flow[i] -= f[t], flow[i^1] += f[t], v = e[i^1];
}
}
}
int main() {
memset(h, -1, sizeof h);
scanf("%d%d%d%d", &n, &m, &s, &t);
int u, v, c, w;
for (int i = 1; i <= m; ++i) {
scanf("%d%d%d%d", &u, &v, &c, &w);
add(u, v, c, w), add(v, u, 0, -w);
}
MCMF();
printf("%lld %lld\n", maxflow, mincost);
return 0;
}
8.20
ABC315A. tcdr:模拟,暴力(红)
点击查看代码
#include <iostream>
using namespace std;
string s;
int main() {
cin >> s;
for (int i = 0; i < s.size(); ++i) {
if (s[i] != 'a' && s[i] != 'e' && s[i] != 'u' && s[i] != 'i' && s[i] != 'o')
cout << s[i];
}
}
ABC315B. The Middle Day:模拟(红)
点击查看代码
#include <iostream>
#include <cstdio>
int d[110];
int m;
int main() {
scanf("%d", &m);
int sum = 0;
for (int i = 1; i <= m; ++i) scanf("%d", &d[i]), sum += d[i]; sum = (sum+1)/2;
int tot = 0;
for (int i = 1; i <= m; ++i) {
tot += d[i];
if (tot >= sum) tot -= d[i], printf("%d %d", i, sum-tot), exit(0);
}
}
ABC315C. Flavors:模拟(橙)
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 3e5+10;
int n;
vector<int> cr[N], nums;
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) {
int f, c; scanf("%d%d", &f, &c);
cr[f].push_back(c);
}
for (int i = 1; i <= n; ++i) {
if (cr[i].size())
sort(cr[i].begin(), cr[i].end());
}
int ans = 0;
for (int i = 1; i <= n; ++i) {
if (!cr[i].size()) continue;
if (cr[i].size() > 1) ans = max(ans, cr[i][cr[i].size()-1]+cr[i][cr[i].size()-2]/2);
nums.push_back(cr[i][cr[i].size()-1]);
}
sort(nums.begin(), nums.end());
ans = max(ans, nums[nums.size()-1]+nums[nums.size()-2]);
printf("%d\n", ans);
}
ABC315D. Magical Cookies:模拟(绿)
用一个桶记录每一行和每一列每个字母的出现次数,记录当前剩余行数 \(ansn\) 和 \(ansm\),每次暴力扫一遍每一行或每一列是否有一个字母可以删除,扫完行和列后一起删除即可。
时间复杂度 \(O(|\Sigma|(n+m)^2)\),其中 \(|\Sigma|=26\)。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 2010;
int n, m; char c[N][N];
int row[N][28], col[N][28]; bool delr[N], delc[N];
int main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m;
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= m; ++j)
cin >> c[i][j], row[i][c[i][j]-'a'] ++, col[j][c[i][j]-'a'] ++;
}
int ansn = n, ansm = m;
for (int i = 1; i <= n+m; ++i) {
vector<int> nowr, nowc;
for (int i = 1; i <= n; ++i) {
if (delr[i]) continue;
for (int j = 0; j < 26; ++j) {
if (row[i][j] == ansm && ansm >= 2)
nowr.push_back(j), delr[i] = 1;
}
}
for (int i = 1; i <= m; ++i) {
if (delc[i]) continue;
for (int j = 0; j < 26; ++j) {
if (col[i][j] == ansn && ansn >= 2)
nowc.push_back(j), delc[i] = 1;
}
}
for (auto c : nowr) {
for (int i = 1; i <= m; ++i) col[i][c] --;
ansn --;
}
for (auto c : nowc) {
for (int i = 1; i <= n; ++i) row[i][c] --;
ansm --;
}
}
cout << ansn*ansm << '\n';
return 0;
}
ABC315E. Prerequisites:拓扑排序(黄)
从 \(1\) 号节点开始 dfs 计算每个点的入度,然后直接跑拓扑排序即可。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 2e5+10;
int n, deg[N]; bool st[N]; vector<int> e[N], nums;
void dfs(int u) {
for (auto v : e[u]) {
deg[v] ++;
if (!st[v]) st[v] = 1, dfs(v);
}
}
void toposort() {
queue<int> q; q.push(1);
while (q.size()) {
int u = q.front(); q.pop();
for (auto v : e[u]) {
deg[v] --;
if (!deg[v]) q.push(v), nums.push_back(v);
}
}
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) {
int s, u; scanf("%d", &s);
for (int j = 1; j <= s; ++j) scanf("%d", &u), e[i].push_back(u);
}
dfs(1), toposort();
for (int i = nums.size()-1; i >= 0; --i) printf("%d ", nums[i]);
return 0;
}
ABC315F. Shortcuts:dp(绿)
令 \(f_{i,j}\) 表示考虑前 \(i\) 个点,跳过 \(j\) 个点时的最小距离(罚时可以最后一起计算),那么状态转移方程为:
初始状态为 \(f_{1,0}=1\)。答案为 \(\min\{f_{n,i}+2^{i-1} \}\)。
直接计算,时间复杂度 \(O(n^3)\),不能通过此题。
注意到本题中 \(x_i,y_i\le 10^4\),那么走完所有点的花费不超过 \(10^4\cdot 10^4\sqrt 2=\sqrt2\cdot 10^8\)。而当我们跳过 \(30\) 个点时,罚时为 \(2^{30}>10^9\),所以我们肯定不能跳超过 \(30\) 个点,即 \(j\) 只需要枚举到 \(\min(29,i-1)\) 即可。
时间复杂度 \(O(nS^2)\),\(S=30\)。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
using namespace std;
typedef pair<int, int> pii;
#define x first
#define y second
#define mpr(a,b) make_pair(a,b)
const int N = 1e4+10;
int n; double f[N][35], ans = 1e9;
pii dots[N];
double get_dist(int x1, int y1, int x2, int y2) {
return sqrt(pow(x1-x2, 2) + pow(y1-y2, 2));
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%d%d", &dots[i].x, &dots[i].y);
f[1][0] = 0;
for (int i = 2; i <= n; ++i) {
for (int j = 0; j < min(30, i-1); ++j) {
f[i][j] = 1e9;
for (int k = i-j-1; k <= i-1; ++k)
f[i][j] = min(f[i][j], f[k][j-(i-k)+1]+get_dist(dots[k].x, dots[k].y, dots[i].x, dots[i].y));
}
}
for (int i = 0; i < min(30, n-1); ++i) ans = min(ans, f[n][i]+((i>0)?pow(2, i-1):0));
printf("%.6f\n", ans);
return 0;
}
ABC315G. G - Ai + Bj + Ck = X (1 <= i, j, k <= N):exgcd(蓝)
首先枚举 \(i\in [1,n]\),把式子化为 \(bj+ck=x-ai\),这样就变成了 exgcd 板子。令 \(d=\gcd(a,b),t=x-ai\),求出方程 \(bj+ck=d\) 的一组特解 \(x_0,y_0\)。那么 \(t \bmod d\ne 0\) 时无解,否则我们可以求出通解 \(x=\dfrac{t}{d}x_0+k\dfrac{c}{d},y=\dfrac{t}{d}y_0-k\dfrac{b}{d}\),由于 \(1\le x,y\le n\),我们有:
- $\left \lceil \dfrac{d-tx_0}{c} \right \rceil \le k\le \left \lfloor \dfrac{dn-tx_0}{c} \right \rfloor $;
- $\left \lceil \dfrac{-dn+ty_0}{b} \right \rceil \le k\le \left \lfloor \dfrac{-d+ty_0}{b} \right \rfloor $
取这两个区间的并集,它们对答案的贡献即为其并集的长度。
注意到负数的情况难以处理,我们可以将分子都加上一个极大值再将减去增加的值,并将所有上取整变为下取整(\(\lceil a/b \rceil=\lfloor (a+b-1)/b \rfloor\))。
点击展开代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
using namespace std;
#define int __int128
typedef long long ll;
const int inf = 1e18;
void write(int x) {
char ch[60];
int len = 0;
if(x < 0)
putchar('-'), x = -x;
do {
ch[len++] = (x%10)^48;
x /= 10;
} while(x);
while(len --) putchar(ch[len]);
putchar(' ');
}
ll n, a, b, c, p, x, y, d, ans;
int exgcd(int a, int b, int &x, int &y) {
if (!b) {x = 1, y = 0; return a;}
int d = exgcd(b, a%b, x, y), t = x;
x = y, y = t - (a/b)*y;
return d;
}
signed main() {
cin >> n >> a >> b >> c >> p;
int x, y, d = exgcd(b, c, x, y);
for (int i = 1; i <= n; ++i) {
int now = p-a*i;
if (now % d || now <= 0) continue;
ans += max((int)0, min((d*(int)n-now*x+c*inf)/(int)c-inf, (-d+now*y+b*inf)/(int)b-inf) -
max((d-now*x+c*inf+c-1)/c-inf, (-d*n+now*y+b*inf+b-1)/b-inf) + 1);
}
write(ans);
return 0;
}
8.21
CF1790F. Timofey and Black-White Tree:(*)根号分治,思维,暴力(蓝)
首先我们有一个结论:
在一条长度为 \(n\) 的链上选取 \(\sqrt n\) 个点,它们之间的最小距离的最大值不超过 \(\sqrt n\)。
这个结论可以推广到树上。
于是我们可以暴力 BFS,每次记录当前点到一个黑色点的最小距离。由于每个点被更改的次数不会超过 \(\sqrt n\) 次,总时间复杂度为 \(O(n\sqrt n)\)。搜索时注意剪枝。
点击查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 2e5+10;
int t, n, s, ans, dist[N], c[N];
vector<int> e[N];
void bfs(int u) {
queue<int> q; q.push(u), dist[u] = 0;
while (q.size()) {
int u = q.front(); q.pop();
if (dist[u] > ans) break; // 继续更新已经没有意义
for (auto v : e[u]) {
if (dist[v] <= dist[u]+1) continue;
dist[v] = dist[u]+1, q.push(v);
}
}
}
void solve() {
scanf("%d%d", &n, &s);
ans = n+1; for (int i = 1; i <= n; ++i) e[i].clear(), dist[i] = 1e9;
for (int i = 1; i < n; ++i) scanf("%d", &c[i]);
for (int i = 1; i < n; ++i) {
int u, v; scanf("%d%d", &u, &v);
e[u].push_back(v), e[v].push_back(u);
}
bfs(s);
for (int i = 1; i < n; ++i) ans = min(ans, dist[c[i]]), bfs(c[i]), printf("%d ", ans); puts("");
}
int main() {
scanf("%d", &t);
while (t -- ) solve();
return 0;
}
P2048 [NOI2010] 超级钢琴:(*)st 表,堆(紫)
考虑固定左端点 \(i\),那么实际上我们要求:
由于 \(s_{i-1}\) 是固定的,所以我们只需要求出 \(\max{s_j}\) 即可,这部分可用 st 表维护。
接下来考虑如何统计答案。我们可以发现,当 \(i\) 为左端点时,若其能对答案产生的最大贡献都未被选上,则其余以 \(i\) 为左端点的答案都不可能被选上。这启发我们用一个节点 \((i,l,r,now,num)\) 表示以 \(i\) 为左端点,右端点在 \([l,r]\) 间的最大贡献 \(num\),其中 \(now\) 为我们选取的点。我们可以将这些节点用一个大根堆(按 \(num\) 排序)维护,当我们取出一个节点时,以 \(i\) 为左端点的区间能对答案产生的最大贡献的右端点要么在 \([l,pos-1]\) 间,要么在 \([pos+1,r]\) 间,这一部分也可以用 st 表维护。
时间复杂度 \(O(k\log (n+k))\)。
点击查看代码
#include <cstdio>
#include <algorithm>
#include <queue>
#include <cmath>
using namespace std;
#define int long long
const int N = 5e5+10;
int n, k, l, r, ans, a[N], s[N], st[N][30];
struct Node {
int i, l, r, pos, num;
bool operator < (const Node &T) const {
return num < T.num;
}
};
int Max(int x, int y) {return (s[x]>s[y])?x:y;}
int query(int l, int r) {
int k = log2(r-l+1);
return Max(st[l][k], st[r-(1<<k)+1][k]);
}
signed main() {
scanf("%lld%lld%lld%lld", &n, &k, &l, &r);
for (int i = 1; i <= n; ++i) scanf("%lld", &a[i]), s[i] = s[i-1]+a[i], st[i][0] = i;
for (int j = 1; (1<<j) <= n; ++j) {
for (int i = 1; i+(1<<j)-1 <= n; ++i)
st[i][j] = Max(st[i][j-1], st[i+(1<<j-1)][j-1]);
}
priority_queue<Node, vector<Node>> q;
for (int i = 1; i <= n; ++i) {
if (i+l-1 > n) break;
int now = query(i+l-1, min(i+r-1, n));
q.push({i, i+l-1, min(i+r-1, n), now, s[now]-s[i-1]});
}
while (k -- ) {
Node t = q.top(); q.pop(); ans += t.num;
int now, i = t.i, l = t.l, r = t.r, pos = t.pos;
if (pos > l) now = query(l, pos-1), q.push(Node{i, l, pos-1, now, s[now]-s[i-1]});
if (pos < r) now = query(pos+1, r), q.push(Node{i, pos+1, r, now, s[now]-s[i-1]});
}
printf("%lld\n", ans);
return 0;
}
8.22
P5201 [USACO19JAN] Shortcut G:最短路(绿)
我们建出以 \(1\) 为根的字典序最小的最短路树,即对于原图中的每个节点 \(v\),其在最短路上的父亲 \(u\) 满足 \(dist_v=dist_u+w(u,v)\) 且 \(u\) 的字典序最小。
统计答案很简单,对于最短路树上的每个点 \(u\),假设其子树内有 \(x\) 个节点,则它的答案为 \((dist_u-t)x\)。
时间复杂度 \(O(n\log m)\)。
点击展开代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <queue>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
const int N = 1e4+10;
int n, m, t, c[N], p[N], dist[N]; ll ans; bool st[N];
vector<pii> e[N];
void dijkstra() {
memset(dist, 0x3f, sizeof dist);
priority_queue<pii, vector<pii>, greater<pii>> q;
q.push({0, 1}), dist[1] = 0;
while (q.size()) {
auto t = q.top(); q.pop();
int u = t.second;
if (st[u]) continue; st[u] = 1;
for (auto edg : e[u]) {
int v = edg.first, w = edg.second;
if (dist[v] > dist[u]+w) {
dist[v] = dist[u]+w, p[v] = u;
q.push({dist[v], v});
} else if (dist[v] == dist[u]+w) p[v] = min(p[v], u);
}
}
}
int dfs(int u) {
int siz = c[u];
for (auto edg : e[u]) siz += dfs(edg.first);
ans = max(ans, (ll)siz*(dist[u]-t));
return siz;
}
int main() {
scanf("%d%d%d", &n, &m, &t);
for (int i = 1; i <= n; ++i) scanf("%d", &c[i]), p[i] = n+1;
for (int i = 1; i <= m; ++i) {
int u, v, w; scanf("%d%d%d", &u, &v, &w);
e[u].push_back({v, w}), e[v].push_back({u, w});
}
dijkstra();
for (int i = 1; i <= n; ++i) e[i].clear();
for (int i = 1; i <= n; ++i) e[p[i]].push_back({i, 1});
dfs(1); printf("%lld\n", ans);
return 0;
}
CF407B. Long Path:(*)dp(蓝)
很有趣的一道题。
首先有一个结论:第一次走到 \(i\) 号房间时,\(1\sim i-1\) 号房间一定都经过了偶数次。证明是显然的。
令 \(f_i\) 表示第一次走到 \(i\) 号房间时经过的门数,考虑如何从 \(i-1\) 转移到 \(i\):
- 第一次走到 \(i-1\) 号房间:\(f_{i-1}\) 步;
- 跳到 \(p_{i-1}\) 号房间:\(1\) 步;
- 跳到 \(k\) 号房间满足 \(p_k=k\),再一直跳到 \(i-1\) 号房间;
- 从 \(i-1\) 号点走到 \(i\) 号点:\(1\) 步。
第 3 步是我们难以直接计算的。观察一下可以发现,我们需要依次跳到 \(x_1=p_{p_{i-1}}\) 号房间,\(x_2=p_{x_1}\) 号房间,以此类推,最后跳到一个房间 \(x_k\) 满足 \(p_{x_k}=x_k\),然后再从 \(x_k\) 往前跳到 \(i\) 号房间。注意到我们第一次跳到 \(p_{i-1}\) 号房间后,我们也需要经过 \(x_1,x_2,\cdots, x_k\) 号房间,并且再从 \(x_k\) 往前跳,即这两条路径是重合的。
容斥一下,容易发现,第 3 步实际的步数为 \(f_{i-1}-f_{p_{i-1}}\)。
所以状态转移方程为:
时间复杂度 \(O(n)\)。
点击展开代码
#include <cstdio>
const int N = 1010, P = 1e9+7;
int n, p[N], f[N]; bool st[N];
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%d", &p[i]);
f[1] = 0;
for (int i = 2; i <= n+1; ++i) f[i] = ((2ll*f[i-1] - f[p[i-1]] + 2) % P + P) % P;
printf("%d\n", f[n+1]);
return 0;
}
P5200 [USACO19JAN] Sleepy Cow Sorting G:树状数组(黄)
可以猜测,若至少需要 \(k\) 步,则有 \(a_k>a_{k+1}\) 且 \(a_{k+1}<a_{k+2}<\cdots<a_n\)。这是因为我们只能改变第一个数的位置,所以我们需要将前 \(k\) 个元素全部操作一遍才能将 \(a_k\) 换到正确的位置上。
考虑如何计算方案。假设当前第一个数为 \(a_i\),我们需要保证操作后数列后半部分的数仍然是递增的,那么需要将它向后移动 \(k-i+(\text{后半部分}\le x\text{的数的数量})\)。树状数组维护即可。
时间复杂度 \(O(n\log n)\)。
点击展开代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 1e5+10;
int n, k, a[N], c[N];
int lowbit(int x) {
return x & -x;
}
void add(int x, int k) {for (int i = x; i <= n; i += lowbit(i)) c[i] += k;}
int query(int x) {
int res = 0;
for (int i = x; i >= 1; i -= lowbit(i)) res += c[i];
return res;
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) {
scanf("%d", &a[i]);
if (a[i] < a[i-1]) k = i-1;
}
printf("%d\n", k);
for (int i = k+1; i <= n; ++i) add(a[i], 1);
for (int i = 1; i <= k; ++i) printf("%d ", query(a[i])+k-i), add(a[i], 1);
return 0;
}
8.23
P2757 [国家集训队] 等差子序列:线段树,哈希(紫)
题目要求判断是否存在一个长度 \(\ge 3\) 的等差子序列,那么我们只需要考虑长度为 \(3\) 的等差子序列是否存在即可。考虑一个中项 \(a_i\),以及公差 \(d\),则以 \(a_i\) 为中项的等差子序列存在,当且仅当 \(a_i-d\) 和 \(a_i+d\) 在 \(a_i\) 异侧。
于是,我们可以建一棵权值线段树,扫一遍 \(a\) 数组,每次对于当前点 \(a_i\),判断以 \(a_i\) 为中心的 01 串是否回文,若回文说明 \(a_i-d\) 和 \(a_i+d\) 都在 \(a_i\) 之前出现过,即不存在以 \(a_i\) 为中心的等差子序列。判断回文的过程可以用字符串哈希实现。
时间复杂度 \(O(Tn\log n)\),大常数选手。
点击展开代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
typedef unsigned long long ull;
const int N = 5e5+10, P = 998244353;
int t, n, a[N]; ull p[N];
struct Node {
int l, r, len; ull val, rval;
} seg[N<<2];
void pushup(Node &u, Node &l, Node &r) {
u.val = l.val * p[r.len] + r.val, u.rval = r.rval * p[l.len] + l.rval;
u.len = l.len + r.len;
}
void build(int u, int l, int r) {
seg[u].l = l, seg[u].r = r, seg[u].val = seg[u].rval = 0;
if (l == r) return (void)(seg[u].len = 1);
int mid = l + r >> 1;
build(u<<1, l, mid), build(u<<1|1, mid+1, r);
pushup(seg[u], seg[u<<1], seg[u<<1|1]);
}
Node query(int u, int l, int r) {
if (seg[u].l >= l && seg[u].r <= r) return seg[u];
int mid = seg[u].l + seg[u].r >> 1; Node res, L, R;
if (r <= mid) return query(u<<1, l, r);
else if (l > mid) return query(u<<1|1, l, r);
else {pushup(res, L=query(u<<1, l, r), R=query(u<<1|1, l, r)); return res;}
}
void modify(int u, int pos, int v) {
if (seg[u].l == pos && seg[u].r == pos) return (void)(seg[u].val = seg[u].rval = v);
int mid = seg[u].l + seg[u].r >> 1;
if (pos <= mid) modify(u<<1, pos, v);
else modify(u<<1|1, pos, v);
pushup(seg[u], seg[u<<1], seg[u<<1|1]);
}
void solve() {
bool check = 0;
scanf("%d", &n); build(1, 1, n);
for (int i = 1; i <= n; ++i) {
scanf("%d", &a[i]);
int len = min(a[i], n-a[i]+1);
Node L = query(1, a[i]-len+1, a[i]), R = query(1, a[i], a[i]+len-1);
if (L.val != R.rval) check = 1;
modify(1, a[i], 1);
}
if (check) puts("Y");
else puts("N");
}
int main() {
p[0] = 1;
for (int i = 1; i <= 500000; ++i) p[i] = p[i-1] * P;
scanf("%d", &t);
while (t -- ) solve();
return 0;
}
CF452F. Permutation:线段树,哈希(紫)
双倍经验。
点击展开代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
typedef unsigned long long ull;
const int N = 3e5+10, P = 998244353;
int t, n, a[N]; ull p[N];
struct Node {
int l, r, len; ull val, rval;
} seg[N<<2];
void pushup(Node &u, Node &l, Node &r) {
u.val = l.val * p[r.len] + r.val, u.rval = r.rval * p[l.len] + l.rval;
u.len = l.len + r.len;
}
void build(int u, int l, int r) {
seg[u].l = l, seg[u].r = r, seg[u].val = seg[u].rval = 0;
if (l == r) return (void)(seg[u].len = 1);
int mid = l + r >> 1;
build(u<<1, l, mid), build(u<<1|1, mid+1, r);
pushup(seg[u], seg[u<<1], seg[u<<1|1]);
}
Node query(int u, int l, int r) {
if (seg[u].l >= l && seg[u].r <= r) return seg[u];
int mid = seg[u].l + seg[u].r >> 1; Node res, L, R;
if (r <= mid) return query(u<<1, l, r);
else if (l > mid) return query(u<<1|1, l, r);
else {pushup(res, L=query(u<<1, l, r), R=query(u<<1|1, l, r)); return res;}
}
void modify(int u, int pos, int v) {
if (seg[u].l == pos && seg[u].r == pos) return (void)(seg[u].val = seg[u].rval = v);
int mid = seg[u].l + seg[u].r >> 1;
if (pos <= mid) modify(u<<1, pos, v);
else modify(u<<1|1, pos, v);
pushup(seg[u], seg[u<<1], seg[u<<1|1]);
}
void solve() {
bool check = 0;
scanf("%d", &n); build(1, 1, n);
for (int i = 1; i <= n; ++i) {
scanf("%d", &a[i]);
int len = min(a[i], n-a[i]+1);
Node L = query(1, a[i]-len+1, a[i]), R = query(1, a[i], a[i]+len-1);
if (L.val != R.rval) check = 1;
modify(1, a[i], 1);
}
if (check) puts("YES");
else puts("NO");
}
int main() {
p[0] = 1;
for (int i = 1; i <= 300000; ++i) p[i] = p[i-1] * P;
t = 1;
while (t -- ) solve();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号