再生希尔伯特空间与核函数讲解

再生希尔伯特空间与核函数讲解

目录

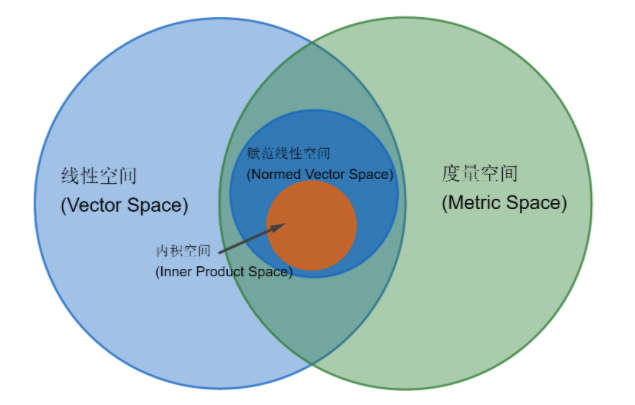
空间

空间的概念就是 空间 = 集合 + 结构

线性空间/向量空间(Linear Space/Vector Space)

线性空间就是 线性空间 = 集合 + 线性结构 ，而其中的线性结构就是 线性结构 = 加法 + 数乘

简单说线性空间就是一系列向量的集合并且只满足加法和标量乘（向量的相乘）操作的集合。

加法运算：首先设一个集合\(V\),在集合\(V\)中定义元素的加法运算：\(\forall x,y\in V\),在\(V\)中都有唯一的一个元素\(\gamma\)与之对应，称为\(x与y\)的和，即\(x+y\).

数乘运算：数乘就是用一个数字去乘，这个数字的来源就是一个数域\(F\)，\(\forall a \in F, x \in V,\)在\(V\)中都有唯一的元素\(\delta\)与之对应，称为\(a与x\)的数量乘积

除了运算，以上的两种运算还要满足下面的八种性质：

加法

  1. \(x+(y+z) = (x+y)+z\)
  2. \(x+y = y+x\)
  3. 存在一个元素\(0\in V\),使得\(x+0 = x\)，\(\forall x \in V\)
  4. \(\forall x \in V\),存在一个元素\(-x\in V\),使得\(x+(-x) = 0\).

数乘

  1. \(1x = x\)
  2. \((ab)x=a(bx)\)

二者都有：

  1. \((a+b)x=ax+bx\)
  2. \(a(x+y)=ax+ay\)

满足以上条件，则称V是数域F上的线性空间或者向量空间，V中的元素称为向量。

度量空间

度量空间 = 集合 + 拓扑结构

给定一个集合\(V\)，在\(V\)上定义一种新的运算：距离：\(V \times V \rightarrow R,\forall x,y \in V,\)在\(R\)中都有唯一的元素\(\delta\)与之对应，称为\(x,y\)之间的距离。

满足的性质：

  1. \(d(x,y)\geqslant0,\forall x,y \in V\)且\(d(x,y)=0\Leftrightarrow x=y\)（非负性）
  2. \(d(x,y)\leqslant d(x,y)+d(y,z)\)（三角不等式）
  3. \(d(x,y)=d(y,x)\)（自反性）

其中\((V,d)\)为度量空间或者距离空间，其中V的元素称为点。

赋范线性空间/范数向量空间

赋范线性空间 = 线性空间 + 范数 ：就是给线性空间穿上拓扑结构的外衣。

设\(V\)是一个实线性空间，对应的数域为\(R\)，在其上定义范数运算\(\Vert·\Vert:V \rightarrow R,\)即\(\forall x \in V,\)在\(R\)中都有唯一的元素\(\delta\)与之对应，称之为x的范数，记为\(\Vert x\Vert\)。

满足的性质：

  1. \(\Vert x\Vert \geqslant 0\)且\(\Vert x\Vert = 0 \Leftrightarrow x=0\)（非负性）
  2. \(\Vert ax\Vert = \vert a\vert \Vert x \Vert, a\in R\)（齐次性）
  3. \(\Vert x+y\Vert \leqslant \Vert x\Vert + \Vert y\Vert, x,y\in V\)（三角不等式）

则称\((V,\Vert ·\Vert)\)为赋范线性空间。

如果我们使用范数来定义距离，即令\(d(x,y)=\Vert x-y\Vert\),则

  1. \(d(x,y)\geqslant0,\forall x,y\in V\)且\(d(x,y)=0\Leftrightarrow x=y\)
  2. \(d(x,y) = \Vert x-z \Vert = \Vert x-y+y-z\Vert \leqslant \Vert x-y\Vert+\Vert y-z\Vert=d(x,y)+d(y,z)\)

所以d是V上的距离，\((V,d)\)是度量空间，赋范线性空间V也具有拓扑结构。

距离与范数的关系

距离是空间中任意两点\(x,y\)满足以下三个条件：

  1. \(d(x,y)\geqslant0,\forall x,y \in V\)且\(d(x,y)=0\Leftrightarrow x=y\)
  2. \(d(x,y)\leqslant d(x,y)+d(y,z)\)
  3. \(d(x,y)=d(y,x)\)

而范数则是空间中的一点到空间零点的距离，满足以下条件：

  1. \(\Vert x\Vert \geqslant 0\)且\(\Vert x\Vert = 0 \Leftrightarrow x=0\)
  2. \(\Vert ax\Vert = \vert a\vert \Vert x \Vert, a\in R\)
  3. \(\Vert x+y\Vert \leqslant \Vert x\Vert + \Vert y\Vert, x,y\in V\)

可以看出范数是在距离的基础上添加了新的约束限制，所以范数与距离的关系可以类似理解为与红富士苹果与苹果的关系。

内积空间(inner product space)

内积空间 = 线性空间 + 内积

给定一个集合\(V\)，在\(V\)上定义一种新的运算：内积：\(V \times V \rightarrow R,\forall x,y \in V,\)在\(R\)中都有唯一的元素\(\delta\)与之对应，称为\(x,y\)之间的内积，记为\((x,y)\)。

满足性质：

  1. \((x,y)\geqslant0\)且\((x,x)=0\Leftrightarrow x=0\)
  2. \((x,y)=(y,x)\)
  3. \((ax,z)=a(x,z),a\in R\)
  4. \((x+y,z)=(x,z)+(y,z)\)

则\((V,(·,·))\)为内积空间。

如果使用内积定义范数，令\(\Vert x \Vert=\sqrt{(x,x)}\)，则

  1. \(\Vert x\Vert\geqslant 0\)且\(\Vert x\Vert=0 \Leftrightarrow 0\)
  2. \(\Vert ax\Vert=\sqrt{(ax,ax)}=\sqrt{a^2(x,x)}=\vert a\vert\Vert x\Vert\)

则\(\Vert x \Vert=\sqrt{(x,x)}\)是线性空间V上的范数，\(V,\sqrt{(·,·)}\)是赋范线性空间。

image-20210201115217550

欧式空间/欧几里得空间(Euclidean Space)

设\(V\)是实数域\(R\)上的线性空间（或称为向量空间），若\(V\)上定义着正定对称双线性型\(g\)（\(g\)称为内积），则\(V\)称为（对于\(g\)的）内积空间或欧几里德空间（有时仅当\(V\)是有限维时，才称为欧几里德空间）。这些数学空间可以被扩展来应用于任何有限维度，而这种空间叫做\(n\)维欧几里得空间（甚至简称\(n\)维空间）或有限维实内积空间。
欧里几何空间可以说是内积空间的引申。

巴拿赫空间

巴拿赫空间 = 赋范空间 + 完备性

希尔伯特空间

在内积空间上扩展，使得内积空间满足完备性，形成希尔伯特空间如下：

希尔伯特空间 = 内积空间 + 完备性

其中完备性的意思就是空间中的极限运算不能跑出该空间，如有理数空间中的\(\sqrt{2}\)的小数表示，其极限随着小数位数的增加收敛到\(\sqrt{2}\)，但\(\sqrt{2}\)属于无理数，并不在有理数空间，故不满足完备性。

一个通俗的理解是把学校理解为一个空间，你从学校内的宿舍中开始一直往外走，当走不动停下来时（极限收敛），发现已经走出学校了（超出空间），不在学校范围内了（不完备了）。希尔伯特就相当于地球，无论你怎么走，都还在地球内（飞出太空除外）。

希尔伯特空间是一个函数空间，即空间中每个元素都是一个函数。

核函数

1.矩阵的特征值分解

在一般的欧氏空间中，我们可以定义一个\(n\times n\)的矩阵的特征值和特征向量。

\[A\mathbf{x}=\lambda \mathbf{x} \]

其中\(\lambda\)是矩阵\(A\)的特征值，而\(\mathbf{x}\)则是对应的特征向量。如果\(A\)有两个不同的特征值\(\lambda_1\)与\(\lambda_2\),对应不同的特征向量\(\mathbf{x_1}\)与\(\mathbf{x_2}\),且\(\lambda_1 \neq\lambda_2\),则有

\[\lambda_1\mathbf{x}^T_1\mathbf{x}_2=\mathbf{x}^T_1A^T\mathbf{x}_2=\mathbf{x}^T_1A\mathbf{x}_2=\lambda_2\mathbf{x}^T_1\mathbf{x}_2 \]

但是由于\(\lambda_1 \neq\lambda_2\)，那么一定有\(\mathbf{x}^T_1\mathbf{x}_2=0\)，即\(\mathbf{x_1}\)与\(\mathbf{x_2}\)正交，即两个特征向量是正交的。

对于矩阵\(A\in \mathcal{R}^{n\times n}\),可以找到n个特征值及其对应的特征向量。则A可以按照下面的形式进行特征值分解

\[A=QDQ^T \]

其中\(Q\)为正交矩阵（\(QQ^T=I\)），\(D=diag(\lambda_1,\lambda_2,...,\lambda_n)\)。

\[A=QDQ^T=(\mathbf{q_1,q_2,...,q_n}) \left\{ \begin{matrix} \lambda_1 & & \\ & \lambda_2 & \\ & & \lambda_3 \end{matrix} \right\} \left\{ \begin{matrix} q_1^T\\ q_2^T\\ ...\\ q_n^T\\ \end{matrix} \right\}\\ =(\lambda_1q_1,\lambda_2q_2,...,\lambda_nq_n) \left\{ \begin{matrix} q_1^T\\ q_2^T\\ ...\\ q_n^T\\ \end{matrix} \right\}\\ =\sum\limits^{n}\limits_{i=1}{\lambda_iq_iq^T_i} \]

这里的\(\{q_i\}^n_{i=1}\)为\(\mathcal{R^n}\)空间中的一组正交基。

当一个矩阵可以进行特征值分解的时候，其特征向量构成了这个\(n\)维空间的一组基底.

2.核函数

每一个函数\(f\)都可以看做一个无限维的向量，那么二元函数\(K(\mathbf{x,y})\)就可以看做是一个无限维的矩阵。如果它满足：

正定性

\[\int\int f(x)K(\mathbf{x,y})f(y)dxdy \geqslant0 \]

对称性

\[K(\mathbf{x,y})= K(\mathbf{y,x}) \]

那么它就是一个核函数。

3.Mercer定理

与矩阵特征值和特征向量类似，核函数存在特征值和特征函数（将函数看做无限维向量）。也就是：

\[\int K(\mathbf{x,y})\psi(\mathbf{x})dx=\lambda\psi(\mathbf{y}) \]

类比于上面的矩阵，对于不同的特征值\(\lambda_1,\lambda_2\),及其对应的特征方程\(\psi_1(\mathbf{x}),\psi_2(\mathbf{x})\)

\[\int \lambda_1 \psi_1(\mathbf{x})\psi_2(\mathbf{x})dx=\int \lambda_2 \psi_2(\mathbf{x})\psi_1(\mathbf{x})dx \]

因此，\(<\psi_1,\psi_2>=\int\psi_1(\mathbf{x})\psi_2(\mathbf{x})dx=0\).即特征方程是正交的。

一个核函数对应无穷个特征值\(\{\lambda_i\}^{\infty}_{i=1}\)和无穷个特征方程\(\{\psi_i\}^{\infty}_{i=1}\)。和矩阵类似，

\[K(\mathbf{x,y})=\sum\limits^{\infty}\limits_{i=0}\lambda_i \psi_i(\mathbf{x})\psi_j(\mathbf{y}) \]

这里\(\psi_i ,\psi_j \geqslant0,i \neq j\)。\(\{\psi_i\}^{\infty}_{i=1}\)是原来函数空间的一组正交基。

4.核函数的作用以及通俗理解

问题：给杜两个向量\(\mathbf{x_i,x_j}\)，目标是要计算它们的内积\(I=<\mathbf{x_i,x_j}>\)。

现在通过某种非线性变换\(\Phi:\mathbf{x\rightarrow \phi(x)}\)被它们映射到一个高维空间中，映射后的变量就变成了\(\phi(x_i),\phi(x_j)\)，映射后的内积变为\(I^{'}=<\phi(x_i),\phi(x_j)>\)。

那么现在要如何计算变换后的内积呢？

传统方法是先计算映射后的向量\(\phi(x_i),\phi(x_j)\)，然后再计算它俩的内积。但是这样做计算很复杂，因为映射到高维空间后的数据维度很高。比如，假设\(\mathbf{x_i,x_j}\)映射之后都是一个(1×10000)维的向量，那么他们的内积计算就需要做10000次加法操作和10000次乘法操作，显然复杂度很高。

那么能不能在原始空间找到一个函数\(K(\mathbf{x_i,x_j})\)使得\(K(\mathbf{x_i,x_j})=<\phi(x_i),\phi(x_j)>\)？如果可以的话，我们就可以在低维空间直接计算\(K(\mathbf{x_i,x_j})\)的值，不需要先把数据映射到高维空间，再通过复杂的计算求解映射后的内积了。这样的函数是存在的，这样的函数叫做核函数。

例子： $$x = (x1, x2, x3, x4); y = (y1, y2, y3, y4)$$

\[f(x) = (x1x1, x1x2, x1x3, x1x4, x2x1, x2x2, x2x3, x2x4, x3x1, x3x2, x3x3, x3x4, x4x1, x4x2, x4x3, x4x4) \]

\(f(y)\)同理。令核函数\(K(\mathbf{x,y})=(<\mathbf{x,y}>)^2\).

\[x = (1, 2, 3, 4); y = (5, 6, 7, 8). \]

不使用核函数：$$f(x) = ( 1, 2, 3, 4, 2, 4, 6, 8, 3, 6, 9, 12, 4, 8, 12, 16) ;$$

\[f(y) = (25, 30, 35, 40, 30, 36, 42, 48, 35, 42, 49, 56, 40, 48, 56, 64) ; \]

\[<f(x), f(y)> = 25+60+105+160+60+144+252+384+105+252+441+672+160+384+672+1024 = 4900.\]

使用核函数：\(K(\mathbf{x,y})=(5+12+21+32)^2=70^2=4900\)

再生核希尔伯特空间

将\(\{\sqrt{\lambda_i}\psi_i\}^{\infty}_{i=1}\)作为一组正交基构建一个希尔伯特空间\(\mathcal{H}\),这个空间中的任何一个函数（向量）都可以表示为这组基的线性组合。如

\[f=\sum\limits^{\infty}\limits_{i=1}f_i\sqrt{\lambda_i}\psi_i \]

则\(f\)就可以表示为\(\mathcal{H}\)中的一个无限维的向量：\(f=(f_1,f_2,...)^T_{\mathcal{H}}\),\(K(\mathbf{x,y})\)表示二元函数或无限维矩阵，\(K(\mathbf{x,·})\)就可以表示矩阵第x行的一元函数或无限维向量，也就是固定核函数的一个参数为x，那么

\[K(\mathbf{x,·})=(\sqrt{\lambda_1}\psi_1(\mathbf{x}),\sqrt{\lambda_2}\psi_2(\mathbf{x}),...)^T_{\mathcal{H}} \]

同样的，

\[K(\mathbf{y,·})=(\sqrt{\lambda_1}\psi_1(\mathbf{y}),\sqrt{\lambda_2}\psi_2(\mathbf{y}),...)^T_{\mathcal{H}} \]

因此，

\[<K(\mathbf{x,·}),K(\mathbf{y,·})>_{\mathcal{H}}=\sum\limits^{\infty}_{i=0}{\lambda_i \psi_i(\mathbf{x})\psi_i(\mathbf{y})}=K(\mathbf{x,y}) \]

以上就是核的可再生性(reproducing)，即用核函数来再生两个函数的内积。也被叫做可再生核希尔伯特空间.

具体定义

设\(\mathcal{H}\)是一个由定义在非空集合\(\mathcal{X}\)上的函数\(f:\mathcal{X}\rightarrow \mathbb{K}\)构成的希尔伯特函数空间，若函数\(k：\mathcal{X}\times\mathcal{X}\rightarrow\mathbb{R}\)满足：

  • \[∀x∈\mathcal{X} ,k(⋅,x)∈\mathbb{K} \]

  • \[∀x∈\mathcal{X},∀f∈\mathcal{H},\left <f,k(⋅,x) \right >_\mathcal{H}=f(x) \]

  • \[∀x,y∈\mathcal{X},k(x,y)=\left <k(⋅,x),k(⋅,y) \right >_\mathcal{H} \]

其中\(<⋅,⋅>_\mathcal{H}\)是内积，则\(k\)称为\(\mathcal{H}\)的再生核函数，\(\mathcal{H}\)称为再生核希尔伯特空间（RKHS）.

距离⟶范数⟶内积

向量空间+范数⟶ 赋范空间+线性结构⟶线性赋范空间+内积运算⟶内积空间+完备性⟶希尔伯特空间

内积空间+有限维⟶欧几里德空间

赋范空间+完备性⟶巴拿赫空间

转载或参考：

posted @ 2021-04-08 09:24  Jason66661010  阅读(1129)  评论(0)  编辑  收藏  举报