图卷积网络

图卷积网络

@

目录

• 图卷积网络
  • 图卷积网络的概述
  • 循环图神经网络
    • 状态更新与输出
    • 不动点理论
    • \(f\)函数的具体实现
    • 模型学习
    • GNN与RNN
    • GNN的局限
  • 门控图神经网络(Gated Graph Neural Network)
    • 状态更新
  • 图卷积网络
    • 图卷积缘起
    • 图卷积框架(Framework)
    • GCN与GNN区别
    • 卷积
    • 空域卷积(Spatial Convolution)
      • 消息传递网络(Message Passing Neural Network)
      • 图采样与聚合(Graph Sample and Aggregate)
    • 频域卷积(Spectral Convolution)⭐⭐⭐
      • 傅里叶变换(Fourier Transform)
      • 傅里叶变换的应用
      • 傅里叶变换的公式
      • 图上的傅里叶变换
    • 频域卷积网络(Spectral CNN)
    • 切比雪夫网络(ChebNet)

图卷积网络的概述

图神经网络的核心工作是对空间域(Spatial Domain)中节点的Embedding进行卷积操作(即聚合邻居Embedding信息)，然而图数据和图像数据的差别在于节点邻居个数、次序都是不定的，因此传统用于图像上的CNN模型中的卷积操作(Convolution Operator)不能直接用在图上，因此需要从频谱域(Spectral Domain)上重新定义这样的卷积操作再通过卷积定理转换回空间域上。

为了在频谱域和空间域中转换，我们借助了傅里叶公式，并且定义了图上傅里叶变换(从空间域变换到频谱域)和图上傅里叶逆变换(从频谱域回到空间域)的变换公式。具体操作是我们将节点的Embedding f(i), i ∈ (1,⋯,N)通过傅里叶正变换从空间域变换到了频谱域\(\hat{f}\)，在频谱域上和卷积核h进行卷积操作，再将变换后的节点Embedding通过傅里叶逆变换回到空间域，参与后续的分类等任务。

循环图神经网络

状态更新与输出

最早的图神经网络是基于一个不动点理论。给定一张图\(G\),每个结点都有自己的特征（节点的特征用\(x_v\)来表示），而且连接两个结点的边也有自己的特征（边的特征使用\(x_{(v,u)}\)来表示结点\(v\)与结点\(u\)之间的边的特征）。GNN 的学习目标就是获得每个结点的图感知隐藏状态\(h_v\)。GNN通过迭代式更新所有结点的隐藏状态来实现，结点\(v\)的隐藏状态按照如下方式更新：

\[h^{t+1}_{v}=f(x_v,x_co[v],h^t_ne[v],x_ne[v]) \]

公式中的\(f\)就是隐藏状态中的状态更新函数，又叫局部转移函数。其中的\(x_co[v]\)表示与结点\(v\)相邻的边的特征，\(x_ne[v]\)表示结点\(v\)的另据节点的特征，\(h^t_ne[v]\)表示邻居结点在t时刻的隐藏状态。

例如上图，假设结点5为中心结点，其隐藏状态的更新函数如图所示。

除了状态更新函数，还需要一个局部输出函数\(g\)，如图。

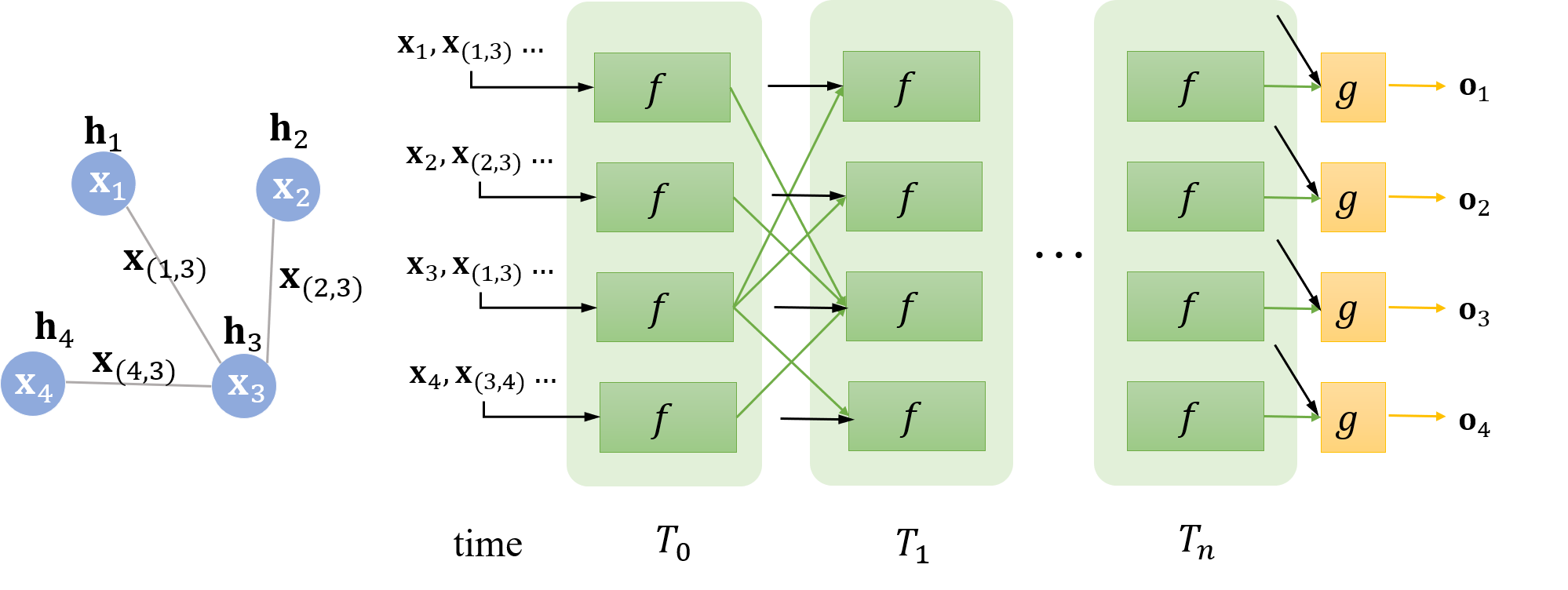
在 T1 时刻，结点 1 的状态接受来自结点 3 的上一时刻的隐藏状态，因为结点 1 与结点 3相邻。直到 Tn 时刻，各个结点隐藏状态收敛，每个结点后面接一个 g 即可得到该结点的输出 o。

对于不同的图来说，收敛的时刻可能不同，因为收敛是通过两个时刻p范数的差值是否小于某个阈值\(\epsilon\)来判定的，如

\[||\mathbf{H}^{t+1}||_{2}-||\mathbf{H}^{t}||_{2}<\epsilon \]

不动点理论

GNN的理论基础就是巴拿赫不动点定理。我们用\(F\)表示若干个\(f\)堆叠得到的一个函数，也称为全局更新函数，则图上所有结点的状态更新公式可以写成：

\[H^{t+1}=F(H^t,X) \]

不动点理论指的是，无论\(H_0\)是什么，只要\(F\)是一个压缩映射，\(H_0\)经过不断迭代都会收敛到某一个固定的点，我们称之为不动点。那压缩映射又是什么呢，一张图可以解释得明明白白：

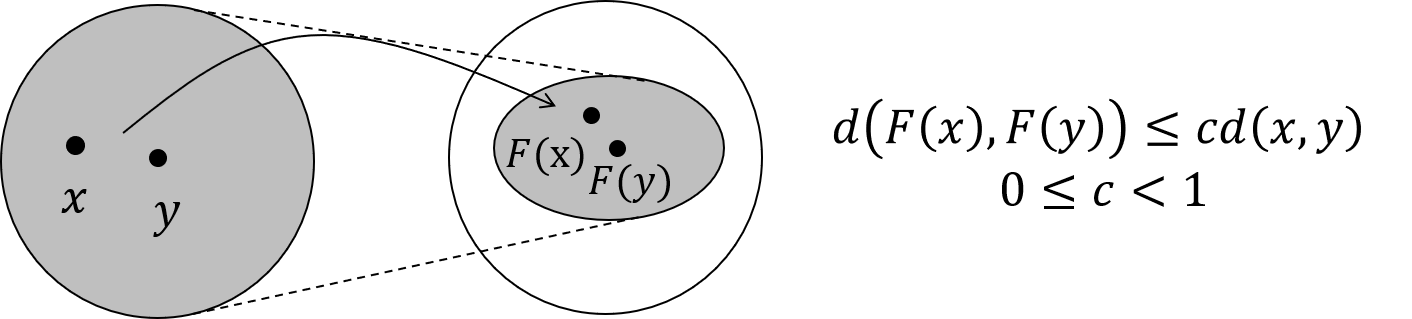
上图的实线箭头就是指映射\(F\),任意两个点\(x,y\)在经过\(F\)这个映射后，分别变成了\(F(x),F(y)\).压缩映射就是指\(𝑑(𝐹(𝑥),𝐹(𝑦))≤𝑐𝑑(𝑥,𝑦), 0≤𝑐<1\),也就是说经过\(F\)变换后的新空间一定比原先的空间要小，原先的空间被压缩了。想象这种压缩的过程不断进行，最终就会把原空间中的所有点映射到一个点上。

\(f\)函数的具体实现

在具体实现中， \(f\) 其实通过一个简单的前馈神经网络(Feed-forward Neural Network)即可实现。比如说，一种实现方法可以是把每个邻居结点的特征、隐藏状态、每条相连边的特征以及结点本身的特征简单拼接在一起，在经过前馈神经网络后做一次简单的加和。

\[h_v^{t+1}=f(x_v,x_co[v] ,h^t_ne[v] ,x_ne[v])\\ =\sum_{u\in ne[v]} FNN([x_v;x_{(u,v)};h_u^t;x_u]) \]

那我们如何保证 f 是个压缩映射呢，其实是通过限制 f 对 H 的偏导数矩阵的大小，这是通过一个对雅可比矩阵(Jacobian Matrix)的惩罚项(Penalty)来实现的。在代数中，有一个定理是: f 为压缩映射的等价条件是 f 的梯度/导数要小于1。这个等价定理可以从压缩映射的形式化定义导出，我们这里使用 \(||x||\) 表示 \(x\) 在空间中的范数(norm)。范数是一个标量，它是向量的长度或者模，\(||x||\) 是 \(x\) 在有限空间中坐标的连续函数。这里把 \(x\) 简化成1维的，坐标之间的差值可以看作向量在空间中的距离，根据压缩映射的定义，可以导出：

\[||F(x)-F(y)||{\leq}c||x-y||, 0\ {\leq}c<1\\ \frac{||F(x)-F(y)||}{||x-y||}{\leq}c\\ \frac{||F(x)-F(x-{\Delta}x)||}{||{\Delta}x||}{\leq}c\\ ||F'(x)||=||\frac{{\partial}F(x)}{{\partial}x}||{\leq}c \]

压缩映射的条件等价于雅可比矩阵的罚项需要满足其范数小于等于c。

根据拉格朗日乘子法，将有约束问题变成带罚项的无约束优化问题，训练的目标可表示成如下形式：

\[J = Loss + \lambda \cdot \max({\frac{||{\partial}FNN||}{||{\partial}\mathbf{h}||}}−c,0), c\in(0,1) \]

模型学习

下面我们来具体叙述一下图神经网络中的损失Loss是如何定义，以及模型是如何学习的。

在前向传播中，模型：

1. 调用\(f\)若干次，比如\(Tn\)次，直到 \(h^{T_n}_{v}\) 收敛。
2. 此时每个结点的隐藏状态接近不动点的解。
3. 对于有监督信息（标签）的结点，将其隐藏状态通过\(g\)得到输出，进而算出模型的损失。

在反向传播中，模型可以直接求出\(f\)和\(g\)对最终的隐藏状态\(h^{T_n}_{v}\)的梯度。然而，因为模型递归调用了\(f\)若干次，为计算 \(f\) 和 \(g\) 对最初的隐藏状态 \(h^0_v\) 的梯度，我们需要同样递归式/迭代式地计算 \(Tn\) 次梯度。最终得到的梯度即为 \(f\) 和 \(g\) 对 \(h^0_v\) 的梯度，然后该梯度用于更新模型的参数。这个算法就是 Almeida-Pineda 算法[9]。

GNN与RNN

相信熟悉 RNN/LSTM/GRU 等循环神经网络的同学看到这里会有一点小困惑，因为图神经网络不论是前向传播的方式，还是反向传播的优化算法，与循环神经网络都有点相像。这并不是你的错觉，实际上，图神经网络与到循环神经网络确实很相似。为了清楚地显示出它们之间的不同，我们用一张图片来解释这两者设计上的不同：

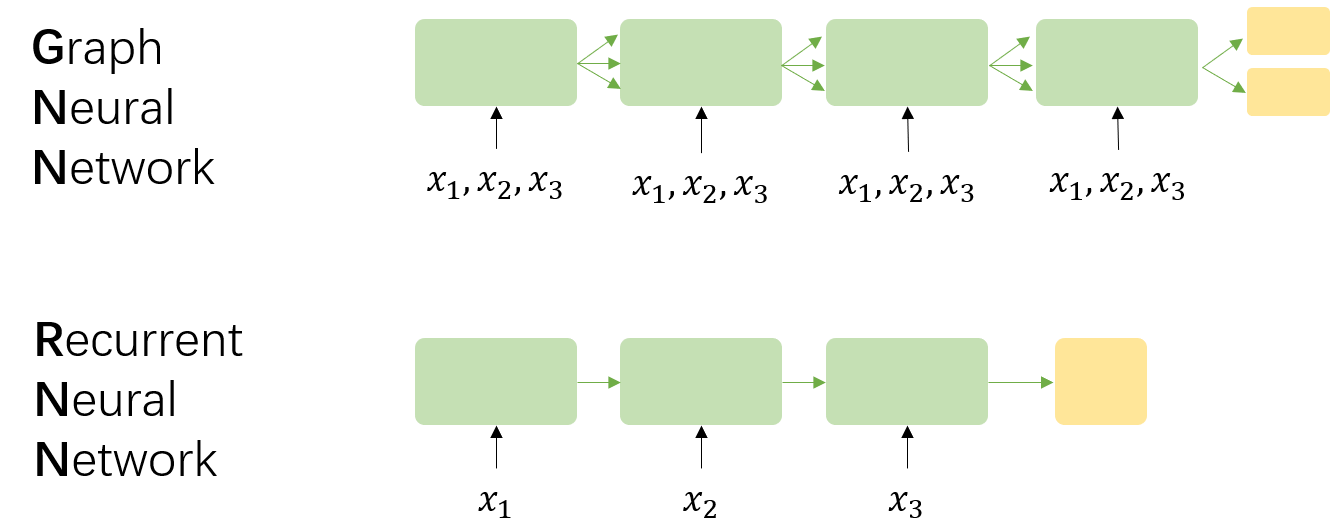
假设在GNN中存在三个结点\(x_1,x_2,x_3\)，相应地，在RNN中有一个序列\((x_1,x_2,x_3)\)。笔者认为，GNN与RNN的区别主要在于4点：

• GNN的基础理论是不动点理论，这就意味着GNN沿时间展开的长度是动态的，是**根据收敛条件**确定的，而RNN沿时间展开的长度就等于序列本身的长度。
• GNN每次时间步的输入都是所有结点v的特征，而RNN每次时间步的输入是该时刻对应的输入。同时，时间步之间的信息流也不相同，前者由边决定，后者则由序列的读入顺序决定。
• GNN采用 AP 算法反向传播优化，而RNN使用BPTT(Back Propogation Through Time)优化。前者对收敛性有要求，而后者对收敛性是没有要求的。
• GNN循环调用 f 的目标是得到每个结点稳定的隐藏状态，所以只有在隐藏状态收敛后才能输出；而RNN的每个时间步上都可以输出，比如语言模型。

GNN的局限

初代GNN，也就是基于循环结构的图神经网络的核心是不动点理论。它的核心观点是通过结点信息的传播使整张图达到收敛，在其基础上再进行预测。收敛作为GNN的内核，同样局限了其更广泛的使用，其中最突出的是两个问题：

• GNN只将边作为一种传播手段，但并未区分不同边的功能。虽然我们可以在特征构造阶段(\(x_{(u,v)}\))为不同类型的边赋予不同的特征，但相比于其他输入，边对结点隐藏状态的影响实在有限。并且GNN没有为边设置独立的可学习参数，也就意味着无法通过模型学习到边的某些特性。
• 如果把GNN应用在图表示的场景中，使用不动点理论并不合适。这主要是因为基于不动点的收敛会导致结点之间的隐藏状态间存在较多信息共享，从而导致结点的状态太过光滑(Over Smooth)，并且属于结点自身的特征信息匮乏(Less Informative)。

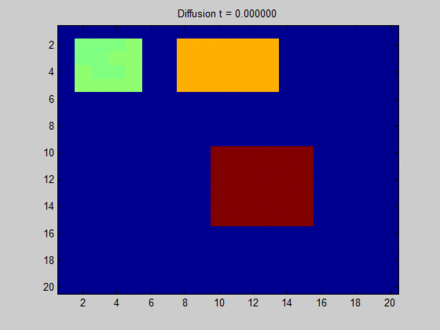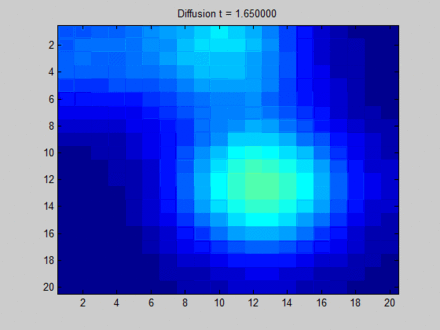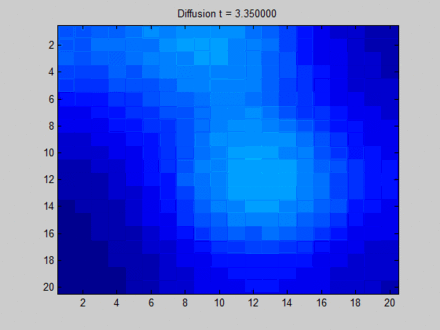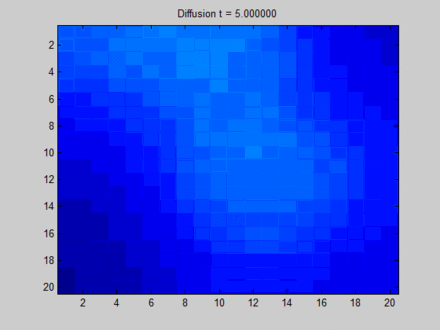
下面这张来自维基百科[13]的图可以形象地解释什么是 Over Smooth，其中我们把整个布局视作一张图，每个像素点与其上下左右以及斜上下左右8个像素点相邻，这决定了信息在图上的流动路径。初始时，蓝色表示没有信息量，如果用向量的概念表达即为空向量；绿色，黄色与红色各自有一部分信息量，表达为非空的特征向量。在图上，信息主要从三块有明显特征的区域向其邻接的像素点流动。一开始不同像素点的区分非常明显，但在向不动点过渡的过程中，所有像素点都取向一致，最终整个系统形成均匀分布。这样，虽然每个像素点都感知到了全局的信息，但我们无法根据它们最终的隐藏状态区分它们。比如说，根据最终的状态，我们是无法得知哪些像素点最开始时在绿色区域。

门控图神经网络(Gated Graph Neural Network)

我们上面细致比较了GNN与RNN，可以发现它们有诸多相通之处。那么，我们能不能直接用类似RNN的方法来定义GNN呢? 于是乎，门控图神经网络(Gated Graph Neural Network, GGNN)就出现了。虽然在这里它们看起来类似，但实际上，它们的区别非常大，其中最核心的不同即是门控神经网络不以不动点理论为基础。这意味着：f 不再需要是一个压缩映射；迭代不需要到收敛才能输出，可以迭代固定步长；优化算法也从 AP 算法转向 BPTT。

状态更新

与图神经网络定义的范式一致，GGNN也有两个过程：状态更新与输出。相比GNN而言，它主要的区别来源于状态更新阶段。具体地，GGNN参考了GRU的设计，把邻居结点的信息视作输入，结点本身的状态视作隐藏状态，其状态更新函数如下:

\[\mathbf{h}^{t+1}_v=\text{GRU}(\mathbf{h}^{t}_v,\sum_{u\in ne[v]} \mathbf{W}_{edge}h_u^t) \]

GGNN还针对不同类型的边引入了可学习的参数\(W\)。每一种 edge 对应一个 \(W_{edge}\)，这样它就可以处理异构图。

但是，仔细对比GNN的GGNN的状态更新公式，细心的读者可能会发现：在GNN里需要作为输入的结点特征 \(x_v\) 没有出现在GGNN的公式中! 但实际上，这些结点特征对我们的预测至关重要，因为它才是各个结点的根本所在。

为了处理这个问题，GGNN将结点特征作为隐藏状态初始化的一部分。那么重新回顾一下GGNN的流程，其实就是这样：

• 用结点特征初始化各个结点的(部分)隐藏状态。
• 对整张图，按照上述状态更新公式固定迭代若干步。
• 对部分有监督信息的结点求得模型损失，利用BPTT算法反向传播求得\(W_{edge}\)和GRU参数的梯度。

图卷积网络

图卷积缘起

为什么研究者们要设计图卷积操作，传统的卷积不能直接用在图上吗？

要理解这个问题，我们首先要理解能够应用传统卷积的图像(欧式空间)与图(非欧空间)的区别。

如果把图像中的每个像素点视作一个结点，如下图左侧所示，一张图片就可以看作一个非常稠密的图；下图右侧则是一个普通的图。阴影部分代表卷积核，左侧是一个传统的卷积核，右侧则是一个图卷积核。卷积代表的含义我们会在后文详细叙述，这里读者可以将其理解为在局部范围内的特征抽取方法。

仔细观察两个图的结构，我们可以发现它们之间有2点非常不一样：

• 在图像为代表的欧式空间中，结点的邻居数量都是固定的。比如说绿色结点的邻居始终是8个(边缘上的点可以做Padding填充)。但在图这种非欧空间中，结点有多少邻居并不固定。目前绿色结点的邻居结点有2个，但其他结点也会有5个邻居的情况。
• 欧式空间中的卷积操作实际上是用固定大小可学习的卷积核来抽取像素的特征，比如这里就是抽取绿色结点对应像素及其相邻像素点的特征。但是因为图里的邻居结点不固定，所以传统的卷积核不能直接用于抽取图上结点的特征。

真正的难点聚焦于邻居结点数量不固定上。那么，研究者如何解决这个问题呢？其实说来也很简单，目前主流的研究从2条路来解决这件事：

• 提出一种方式把非欧空间的图转换成欧式空间。
• 找出一种可处理变长邻居结点的卷积核在图上抽取特征。

图卷积的本质是想找到适用于图的可学习卷积核。

图卷积框架(Framework)

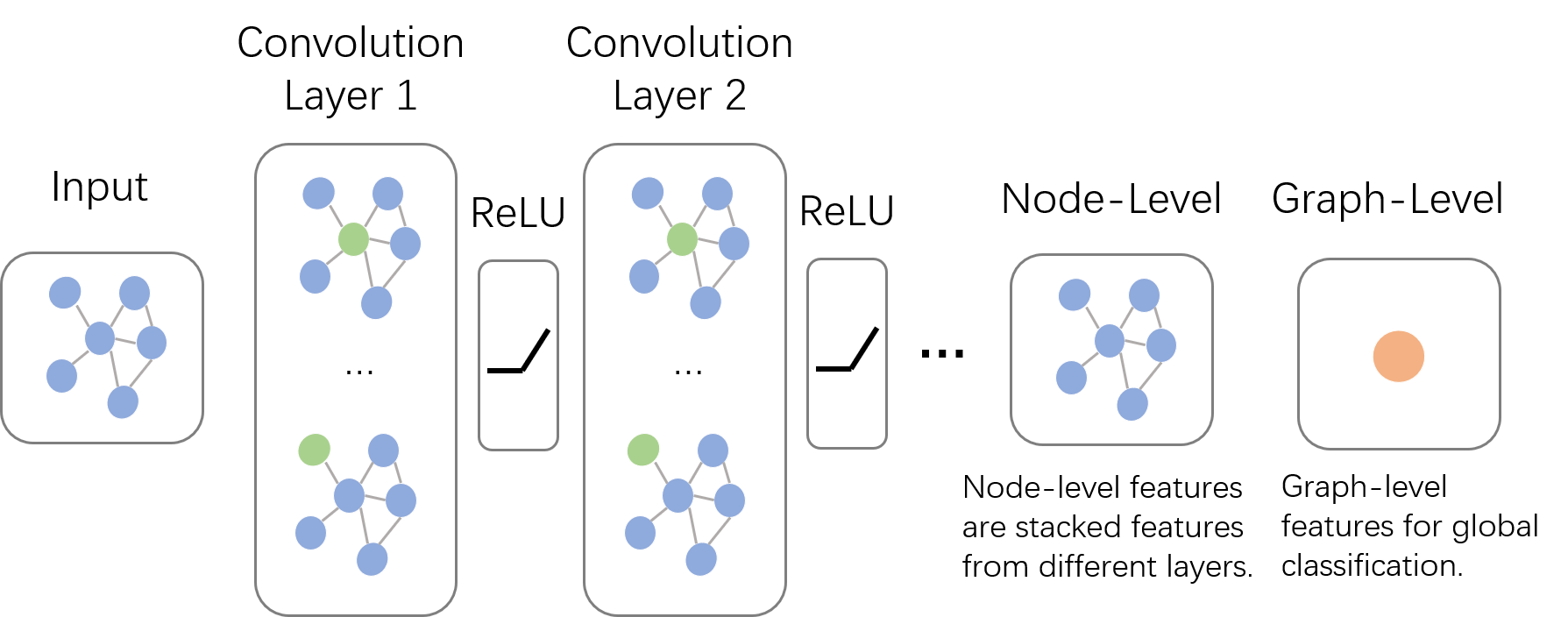
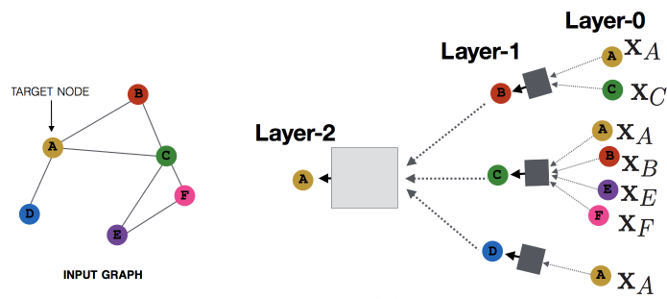
如下图所示，输入的是整张图，在Convolution Layer 1里，对每个结点的邻居都进行一次卷积操作，并用卷积的结果更新该结点；然后经过激活函数如ReLU，然后再过一层卷积层Convolution Layer 2与一层激活函数；反复上述过程，直到层数达到预期深度。与GNN类似，图卷积神经网络也有一个局部输出函数，用于将结点的状态(包括隐藏状态与结点特征)转换成任务相关的标签，本文中笔者称这种任务为Node-Level的任务；也有一些任务是对整张图进行分类的，本文中笔者称这种任务为Graph-Level的任务。卷积操作关心每个结点的隐藏状态如何更新，而对于Graph-Level的任务，它们会在卷积层后加入更多操作。本篇博客主要关心如何在图上做卷积，至于如何从结点信息得到整张图的表示，我们将在下一篇系列博客中讲述。

GCN与GNN区别

多说一句，GCN与GNN乍看好像还挺像的。为了不让读者误解，在这里我们澄清一下它们根本上的不同：GCN是多层堆叠，比如上图中的Layer 1和Layer 2的参数是不同的；GNN是迭代求解，可以看作每一层Layer参数是共享的。

卷积

正如我们在上篇博客的开头说到的，图卷积神经网络主要有两类，一类是基于空域的，另一类则是基于频域的。通俗点解释，空域可以类比到直接在图片的像素点上进行卷积，而频域可以类比到对图片进行傅里叶变换后，再进行卷积。傅里叶变换的概念我们先按下不讲，我们先对两类方法的代表模型做个大概介绍。

基于空域卷积的方法直接将卷积操作定义在每个结点的连接关系上，它跟传统的卷积神经网络中的卷积更相似一些。

基于频域卷积的方法则从图信号处理起家。

空域卷积(Spatial Convolution)

空域卷积与深度学习中的卷积的应用方式类似，其核心在于聚合邻居结点的信息。比如说，一种最简单的无参卷积方式可以是：将所有直连邻居结点的隐藏状态加和，来更新当前结点的隐藏状态。

这里非参式的卷积只是为了举一个简单易懂的例子，实际上图卷积在建模时需要的都是带参数、可学习的卷积核。

消息传递网络(Message Passing Neural Network)

MPNN是一种空域卷积的形式化框架：它将空域卷积分解为两个过程：消息传递与状态更新操作。

将结点\(v\)的特征\(x_v\)作为其隐藏状态的初始态\(h^0_v\)后，空域卷积对隐藏状态的更新由如下公式表示：

\[\mathbf{h}_{v}^{l+1}=U_{l+1}(\mathbf{h}_v,\sum_{u{\in}ne[v]}M_{l+1}(\mathbf{h}_v^l,\mathbf{h}_u^l,\mathbf{x}_{vu})) \]

其中\(l\)代表图卷积的第\(l\)层，上式的物理意义是：收到来自每个邻居的的消息\(M_{l+1}\)后，每个结点如何更新自己的状态。

MPNN示意图：

图采样与聚合(Graph Sample and Aggregate)

MPNN有个致命的缺陷，那就是卷积操作针对的对象是整张图，也就意味着要将所有结点放入内存/显存中，才能进行卷积操作。但对实际场景中的大规模图而言，整个图上的卷积操作并不现实。

于是我们需要一个图中结点的采样方法进行学习。

GraphSage利用采样(Sample)部分结点的方式进行学习。当然，即使不需要整张图同时卷积，GraphSage仍然需要聚合邻居结点的信息，即论文中定义的aggregate的操作。这种操作类似于MPNN中的消息传递过程。

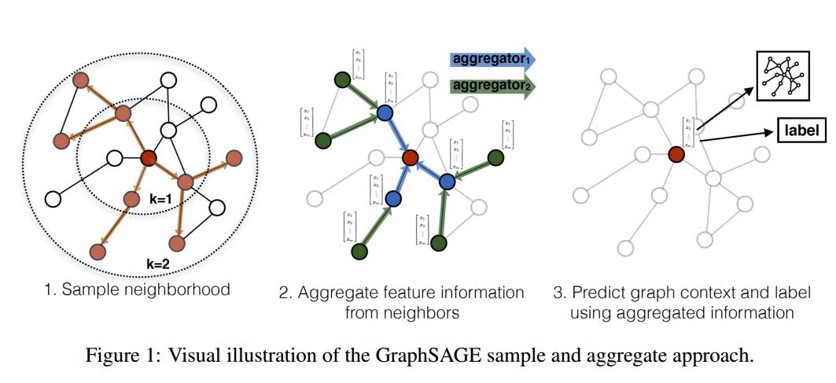
具体地，GraphSage中的采样过程分为三步:

1. 在图中随机采样若干个结点，结点数为传统任务中的batch_size。对于每个结点，随机选择固定数目的邻居结点(这里邻居不一定是一阶邻居，也可以是二阶邻居)构成进行卷积操作的图。
2. 将邻居结点的信息通过aggregate函数聚合起来更新刚才采样的结点。
3. 计算采样结点处的损失。如果是无监督任务，我们希望图上邻居结点的编码相似；如果是监督任务，即可根据具体结点的任务标签计算损失。

最终，GraphSage的状态更新公式如下：

\[\mathbf{h}_{v}^{l+1}=\sigma(\mathbf{W}^{l+1}\cdot aggregate(\mathbf{h}_v^l,\{\mathbf{h}_u^l\}),{\forall}u{\in}ne[v]) \]

频域卷积(Spectral Convolution)⭐⭐⭐

空域卷积非常直观地借鉴了图像里的卷积操作，但据笔者的了解，它缺乏一定的理论基础。而频域卷积则不同，相比于空域卷积而言，它主要利用的是图傅里叶变换(Graph Fourier Transform)实现卷积。简单来讲，它利用图的拉普拉斯矩阵(Laplacian matrix)导出其频域上的的拉普拉斯算子，再类比频域上的欧式空间中的卷积，导出图卷积的公式。虽然公式的形式与空域卷积非常相似，但频域卷积的推导过程却有些艰深晦涩。接下来我们将攻克这部分看起来很难的数学公式，主要涉及到傅里叶变换(Fourier Transform)和拉普拉斯算子(Laplacian operator)。即使读者没有学过任何相关知识也不要紧，笔者将尽可能用形象的描述解释每个公式的涵义，让读者能感悟这些公式的美妙之处。

傅里叶变换(Fourier Transform)

傅里叶变换(Fourier Transform, FT)会将一个在空域(或时域)上定义的函数分解成频域上的若干频率成分。换句话说，傅里叶变换可以将一个函数从空域变到频域。先抛开傅里叶变换的数学公式不谈，用 \(F\) 来表示傅里叶变换的话，我们先讲一个很重要的恒等式：

\[(f*g)(t)=F^{-1}[F[f(t)]{\odot}F[g(t)]] \]

这里的\(F^{-1}\)表示傅里叶逆变换，\(\odot\)表示哈达玛乘积，指的是两个矩阵(或向量)的逐点乘积。仔细观察上面这个公式，它的直观含义可以用一句话来概括：空(时)域卷积等于频域乘积。简单来说就是，如果要算 \(f\) 与 \(g\) 的卷积，可以先将它们通过傅里叶变换变换到频域中，将两个函数在频域中相乘，然后再通过傅里叶逆变换转换出来，就可以得到 \(f\) 与 \(g\) 的卷积结果。下面的动图形象地展示了傅里叶变换的过程，这里我们把函数 \(f\) 傅里叶变换后的结果写作 \(\hat{f}\).

傅里叶变换的应用

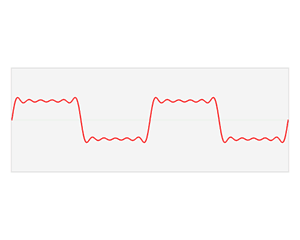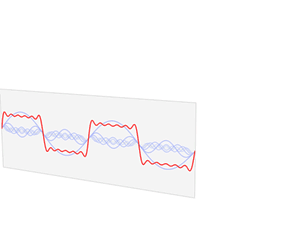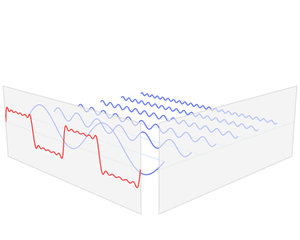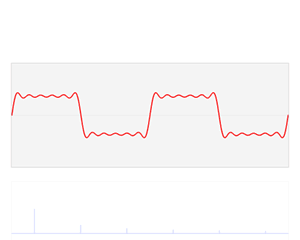
一个简单的应用是给图像去除一些规律噪点。比如说下面这个例子。

在傅里叶变换前，图像上有一些规律的条纹，直接在原图上去掉条纹有点困难，但我们可以将图片通过傅里叶变换变到频谱图中，频谱图中那些规律的点就是原图中的背景条纹。

只要在频谱图中擦除这些点，就可以将背景条纹去掉，得到下图右侧的结果。

---

傅里叶变换还凭借上面的恒等式，在加速卷积运算方面有很大的潜力，快速傅里叶变换(Fast Fourier Transform)也是由此而生。实际上呢，现在大家最常用的卷积神经网络，完全可以搭配傅里叶变换。下面这张图就表示了一个普通的卷积神经网络如何与傅里叶变换搭配，其中的 IFFT 即 快速傅里叶变换的逆变换(Inverse Fast Fourier Transform：

但是目前为什么不使用快速傅里叶变换来加速卷积操作？因为目前我们常用的卷积操作中的卷积核都比较小，如1，3，5，本来卷积消耗的时间就比较少，如果加上傅里叶变换与逆傅里叶变换可能时间并不会有明显的缩减。

傅里叶变换的公式

\[\hat{f}(t)={\int}f(x){\exp}^{-2{\pi}ixt}dx \]

其中\(i=\sqrt{-1}\),t表示任意实数。

\({\exp}^{-2{\pi}ixt}\)的物理意义是图上类比构造傅里叶变换的关键。这个式子实际上是拉普拉斯算子\(\Delta\)的广义特征函数。

拉普拉斯算子(Laplacian operator) 的物理意义是空间二阶导，准确定义是：标量梯度场中的散度，一般可用于描述物理量的流入流出。比如说在二维空间中的温度传播规律，一般可以用拉普拉斯算子来描述。

为什么是特征函数呢，我们这里根据拉普拉斯算子的定义来稍微推导一下。众所周知，特征向量需要满足的定义式是：对于矩阵\(A\)，其特征向量满足的条件应是矩阵与特征向量\(x\)做乘法的结果，与特征向量乘标量\(\lambda\)的结果一样，即满足如下等式:

\[Ax=\lambda x \]

稍微推导一下即可知道，拉普拉斯算子作用在\({\exp}^{-2{\pi}ixt}\)确实满足以上特征向量的定义:

\[∆{\exp}^{-2{\pi}ixt}=\frac{{\partial}^2}{{\partial}t^2}{\exp}^{-2{\pi}ixt}={-4{\pi}^2x^2}{\exp}^{-2{\pi}ixt} \]

傅里叶变换公式的本质其实是将函数\(f(t)\)映射到了以\(\{{\exp}^{-2{\pi}ixt}\}\)为基向量的空间中。

图上的傅里叶变换

在图上，我们去哪找拉普拉斯算子\(\Delta\)与\({\exp}^{-2{\pi}ixt}\)呢？学者找到了图的拉普拉斯矩阵与其特征向量来作为二者的替代品。拉普拉斯矩阵，其实是度矩阵\(D\)(度矩阵是对角阵，对角上的元素为各个顶点的度。顶点vi的度表示和该顶点相关联的边的数量。)减去邻接矩阵\(A\)：\(L=D-A\)

无向图的拉普拉斯矩阵的性质

（1）拉普拉斯矩阵是半正定矩阵。（最小特征值大于等于0） （2）特征值中0出现的次数就是图连通区域的个数 （3）最小特征值是0，因为拉普拉斯矩阵（普通形式：L=D−A）每一行的和均为0，并且最小特征值对应的特征向量是每个值全为1的向量 （4）最小非零特征值是图的代数连通度。

为什么GCN要用拉普拉斯矩阵

(1)拉普拉斯矩阵是对称矩阵，可以进行特征分解（谱分解），这就和GCN的spectral domain对应上了

(2)拉普拉斯矩阵只在中心顶点和一阶相连的顶点上（1-hop neighbor）有非0元素，其余之处均为0

(3)通过拉普拉斯算子与拉普拉斯矩阵进行类比。由于卷积在傅里叶域的计算相对简单，为了在graph上做傅里叶变换，需要找到graph的连续的正交基对应于傅里叶变换的基，因此要使用拉普拉斯矩阵的特征向量。

拉普拉斯矩阵谱分解

矩阵的特征分解，对角化，谱分解都是同一个概念，是指将矩阵分解为由其特征值和特征向量表示的矩阵乘积的方法。只有含有n个线性无关的特征向量的n维方阵才可以进行特征分解。

拉普拉斯矩阵是半正定矩阵，有如下三个性质：

1. 是实对称矩阵，有n个线性无关的特征向量（半正定矩阵本身就是对称矩阵，半正定矩阵_百度百科）
2. 对阵矩阵的特征向量相互正交，即所有特征向量构成的矩阵为正交矩阵
3. 半正定矩阵的所有的特征值非负

性质1告诉我们拉普拉斯矩阵可以分解为\(L=U\Lambda U^{-1}\)，其中\(\Lambda\)是n个特征值组成的对角阵，性质2告诉我们\(U\)是正交矩阵，即\(U^{-1}=U^{T}\)，于是得到下面的公式（1）

频域卷积的前提条件是图必须是无向图，那么L就是一个对称矩阵，所以它可以按照如下公式分解：

\[L = U{\Lambda}U^{T} \tag 1\\ U = (u_1, u_2,{\cdots},u_n)\\ {\Lambda}=\left[ \begin{matrix} {\lambda}_1 & ... & 0 \\ ... & ... & ... \\ 0 & ... & {\lambda}_n \end{matrix} \right] \]

那么，根据上面卷积与傅里叶结合的变换公式，图上频域卷积的公式便可以写成:

\[\hat{f}(t)={\sum}_{n=1}^{N}f(n)u_t(n) \]

如果在整个图的\(N\)个结点上一起做卷积，就可以得到整张图上的卷积如下：

\[{\hat{f}}=\left[ \begin{matrix} {\hat{f}}(1) \\ ... \\ {\hat{f}}(N) \end{matrix} \right]=U^Tf \]

让我们重新审视一下欧式空间上的卷积和图上的卷积，即可明白图上的卷积与传统的卷积其实非常相似，这里 \(f\) 都是特征函数，\(g\) 都是卷积核：

\[(f*g)=F^{-1}[F[f]{\odot}F[g]]\\ (f{*}g)=U(U^Tf{\odot}U^Tg)=U(U^Tg{\odot}U^Tf) \]

如果把 \(U^Tg\) 整体看作可学习的卷积核，这里我们把它写作 \(g_θ\)。最终图上的卷积公式即是：

\[o = (f*_{G}g)_{\theta} = Ug_{\theta}U^Tf \]

频域卷积网络(Spectral CNN)

我们上面推导的这个 \(g_θ\) 就是首个提出的频域卷积神经网络的卷积核.假设\(l\)层的隐藏状态为\(h^l{\in}{R}^{N{\times}d_l}\),类似的第\(l+1\)层为\(h^{l+1}{\in}{R}^{N{\times}d_{l+1}}\).频域卷积层的状态更新计算公式如下：

\[h^{l+1}_{:,j}={\sigma}(U{\sum}_{i=1}^{d_l}{\Theta}^l_{i,j}U^Th^l_{:,i})\\ {\Theta}^l_{i,j}=g_{\theta}= \left[ \begin{matrix} {\theta}_1 & ... & 0 \\ ... & ... & ... \\ 0 & ... & {\theta}_N \end{matrix} \right] \]

这里的\({\Theta}^l_{i,j}\)可以类比全连接神经网络中的权重\(w_{i,j}\).

切比雪夫网络(ChebNet)

基本的频域卷积网络要计算拉普拉斯矩阵所有的特征值和特征向量，计算量巨大。在论文[16]中提出了切比雪夫网络，它应用切比雪夫多项式(Chebyshev polynomials)来加速特征矩阵的求解。假设切比雪夫多项式的第k项是 \(T_k\), 频域卷积核的计算方式如下：

\[g_{\theta}={\sum}_{k=0}^{K-1}{\theta}_{k}T_{k}(\tilde{\Lambda}), \text{where}\ \tilde{\Lambda}=\displaystyle\frac{2\Lambda}{\lambda_{max}}-I_N \]

其中的\(T_k\)可以由切比雪夫多项式的定义得来:\(T_k(x)=2xT_{k-1}(x)-T_{k-2}(x)\),递推式的前两项为\(T_0(x)=1\)与\(T_1(x)=x\)。\(\tilde{\Lambda}\)的作用是让特征向量矩阵归一化到【-1，1】之间。

转载：

https://www.cnblogs.com/SivilTaram/p/graph_neural_network_1.html

https://luweikxy.gitbook.io/machine-learning-notes/graph-neural-networks/graph-convolutional-networks/gcn-comprehensive-understand