RNN

RNN

目录

sequence representation

出现原因

他们都只能单独的取处理一个个的输入，前一个输入和后一个输入是完全没有关系的。但是，某些任务需要能够更好的处理序列的信息，即前面的输入和后面的输入是有关系的。比如，当我们在理解一句话意思时，孤立的理解这句话的每个词是不够的，我们需要处理这些词连接起来的整个序列；当我们处理视频的时候，我们也不能只单独的去分析每一帧，而要分析这些帧连接起来的整个序列。

文本信息的表达方式

【文字或者是单词的数量，数据编码的方式】

编码方式

one-hot编码：

image-20200911105656472

但是当文字或者是单词数量变多的时候，该编码方式比较稀疏，维度较高，成本较大

semantic similarity语义相关性

根据一些单词语义的相关性以及相反性来进行连接

添加了batch的表达方式：

【word_num, b , word_vec】

【b , word_num, word_vec】

例子

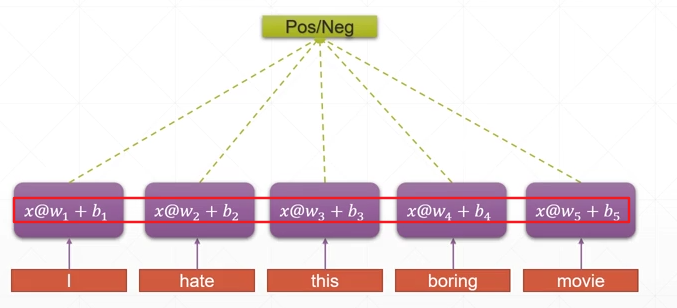
表达 i hate this boring movie

每个单词的表示方法：【100】（假设一共有100个单词）

然后这个句子的表示方法：【5，100】

通过提取每个单词的语义特【2】之后汇总【5，2】来表示这个语义。

缺点：

  1. 在生活中的小说、一段文字中单词较多，w、b的参数较多

  2. 没有上下文的语义联系，通过一个单词一个单词进行分析是不高效、不智能的，所以需要存储一个语境信息

weight sharing

将w、b参数不分为若干个，而是使用一个统一的参数来对整个句子进行分析提取语义特征——weight sharing来解决过多的参数问题

​ Snipaste_2020-09-11_16-44-03

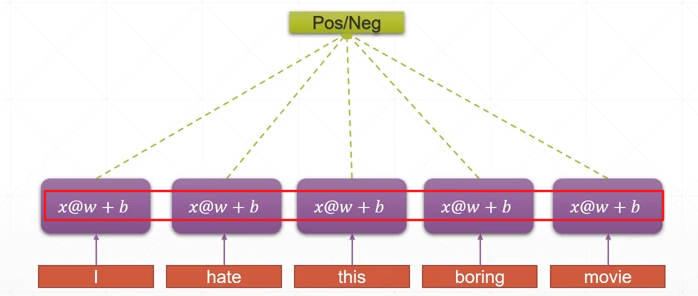
Snipaste_2020-09-11_16-44-23

consistent memory

在进行下一个单元的提取的时候，不但要输入这个单元的数据，还要输入上一个单元的语义信息，这样的话就相当于有一个单元一直提供之前的语义信息（在这样的传递下前面的语义信息是在积累的），通过这一次的输入以及上一次的语义信息来进行网络的更新。

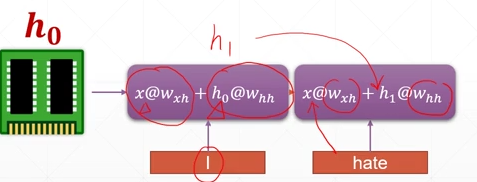
image-20200912090453011

folded model

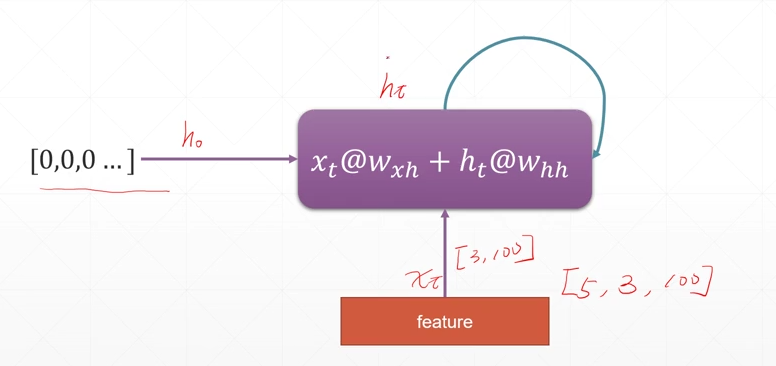
image-20200912091637247

（其中的\(X_t\)表示本次的数据特征，\(h_0\)表示最开始的初始化特征，而\(h_t\)表示前一次的语义信息）

unfolded model

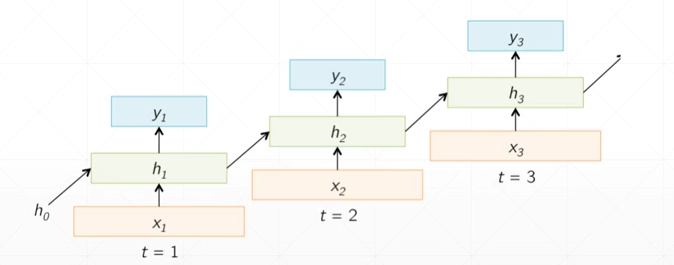
image-20200912092157501

其中的\(h_t\)可以只是上一次的语义信息，也可以是全部的语义信息的汇总，也可以是中间的语义信息，比较灵活。

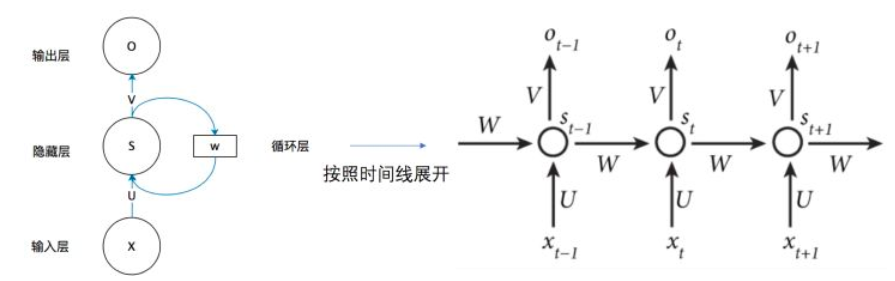
image-20200912144734346

nn.RNN

input_size:是word embedding的维度

hidden_size:是memory的size

forward函数：是一步到位的，例如【5，3，100】5个单词不是将数据喂5次，而是一次到位

out,ht = forward(x,h0)

其中h0表示【layer层数，batch，feature数(hidden_size)】

ht表示最后的一个时间语义输出【layer层数，batch数，feature数】

out表示所有的语义输出【单词数，batch数，feature数】

例子：

import torch
rnn = torch.nn.RNN(input_size=100,hidden_size=20,num_layers=1)
print(rnn)

x = torch.randn(10,3,100)#可以理解为一句话10个单词，一共3句话
out,h = rnn(x,torch.zeros(1,3,20))
print(out.shape,h.shape)

RNN(100, 20)
torch.Size([10, 3, 20]) torch.Size([1, 3, 20])

如果RNN是两层的话，ht【2，batch，feature】（纵向）

out还是【10，batch，feature】（横向）

层数变多，纵向发生变化，但是横向的out还是不变的

时间序列预测实战

目标：预测sin函数曲线的走向

import numpy as np
import torch
import torch.nn as nn
import torch.optim as optim
from matplotlib import pyplot as plt

num_time_steps = 51#点的数量
input_size = 1#由于是散点，不是单词、汉字，所以数据的 embedding的维度为1
hidden_size = 16
output_size = 1
lr = 0.01



class Net(nn.Module):
    def __init__(self):
        super(Net,self).__init__()
        self.rnn = nn.RNN(
            input_size = input_size,
            hidden_size = hidden_size,
            num_layers=1,
            batch_first=True#表示是另外一种表示方法，batch大小在最前
        )
        self.linear = nn.Linear(hidden_size,output_size)

    def forward(self,x,hidden_prev):
        out,hidden_prev = self.rnn(x,hidden_prev)
        out = out.view(-1,hidden_size)#[1,seq,h]-->[seq,h]
        out = self.linear(out)#[seq,h]-->[seq,1]
        out = out.unsqueeze(dim=0)#插入一个维度：要与y进行比较（使用MSE）
        return out,hidden_prev

model = Net()
criteron = nn.MSELoss()
optimizer = optim.Adam(model.parameters(),lr)

hidden_prev = torch.zeros(1,1,hidden_size)

for iter in range(6000):
    start = np.random.randint(3, size=1)[0]
    time_steps = np.linspace(start, start + 10, num_time_steps)
    data = np.sin(time_steps)
    data = data.reshape(num_time_steps, 1)
    x = torch.tensor(data[:-1]).float().view(1, num_time_steps - 1, 1)
    y = torch.tensor(data[1:]).float().view(1, num_time_steps - 1, 1)

    output,hidden_prev = model(x,hidden_prev)
    hidden_prev = hidden_prev.detach()

    loss = criteron(output,y)
    model.zero_grad()
    loss.backward()
    optimizer.step()

    if iter % 100 ==0:
        print('iteration :{} loss {}'.format(iter,loss.item()))



start = np.random.randint(3, size=1)[0]
time_steps = np.linspace(start, start + 10, num_time_steps)
data = np.sin(time_steps)
data = data.reshape(num_time_steps, 1)
x = torch.tensor(data[:-1]).float().view(1, num_time_steps - 1, 1)
y = torch.tensor(data[1:]).float().view(1, num_time_steps - 1,)

predictions = []
input = x[:,0,:]#[batch_size  seq  feature] --> [batch_size  feature]

for _ in range(x.shape[1]):
    input = input.view(1,1,1)#[batch_size  feature] --> [batch_size 1  feature] 意思就是将点数量的那个维度设为1，然后通过这个点以及隐藏层来进行下一个点的预测
    (pred,hidden_prev) = model(input,hidden_prev)
    input = pred
    predictions.append(pred.detach().numpy().ravel()[0])

x = x.data.numpy().ravel()
y = y.data.numpy()
plt.scatter(time_steps[:-1],x.ravel(),s=90)
plt.plot(time_steps[:-1],x.ravel())

plt.scatter(time_steps[1:],predictions)
plt.show()
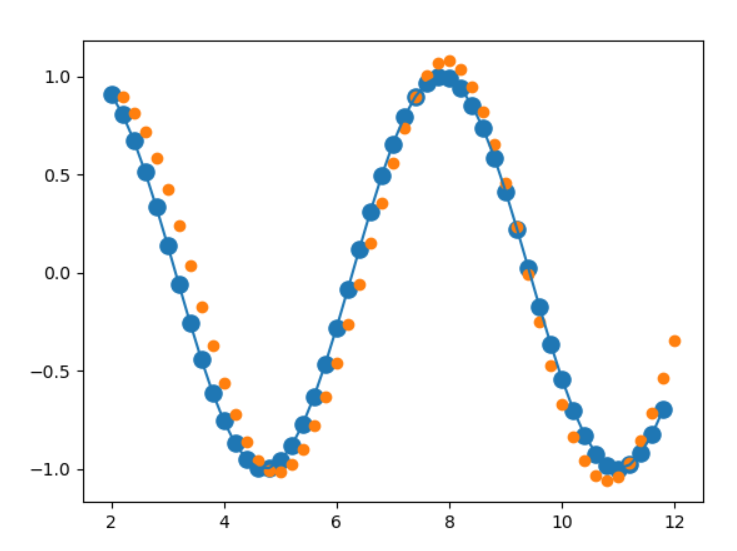
image-20200913150314114

梯度爆炸与梯度弥散

RNN中的\(W_{hh}^k\)在进行k次方的变换后可能变为一个非常大的数，也可能是一个非常小的数

梯度爆炸

loss在逐渐减小的过程中突然变大

解决方法：

检测每个参数的grad，当grad大于自己设定的阈值的时候，我们使用它的tensor除以他自己的模，再乘以自己设定的阈值，这样tensor的方向不变，但是大小变为自己设定的最大值（注意是对参数的grad操作，不是对参数本身操作）

例子：

loss.backward()

for p in model.parameters():
    print(p.grad.norm())#norm()返回向量 v 的欧几里德范数。此范数也称为 2-范数、向量模或欧几里德长度。
	torch.nn.utils.clip_grad_norm_(p,10)

optimizer.step()

梯度消失

由于网络较深等原因导致梯度在回传的时候，后面的层由于梯度较大效果较好，但是前面的层由于计算的原因梯度接近于0，长时间得不到更新，几乎停止了训练。

解决方法：LSTM

LSTM(long short-term memory)

虽然RNN有一个收集所有语义的memory（short term memory），但是实际上它还是对于距离现在时间线较近的word的语义提取较好，离得较远的语义提取汇总较差

原RNN结构

image-20200913181706129

现LSTM结构

image-20200913181730412

LSTM 有通过精心设计的称作为“门”的结构来去除或者增加信息到细胞状态的能力。门是一种让信息选择式通过的方法。他们包含一个 sigmoid 神经网络层和一个 pointwise 乘法操作。

image-20200913181912241

Sigmoid 层输出 0 到 1 之间的数值，描述每个部分有多少量可以通过。0 代表“不许任何量通过”，1 就指“允许任意量通过”！

LSTM 拥有三个门，来保护和控制细胞状态。

逐步理解 LSTM

第一步——遗忘

在我们 LSTM 中的第一步是决定我们会从细胞状态中丢弃什么信息。这个决定通过一个称为忘记门层完成。该门会读取\(h_{t-1}\)和\(x_t\)，输出一个在 0 到 1 之间的数值给每个在细胞状态\(C_{t-1}\)中的数字。1 表示“完全保留”，0 表示“完全舍弃”。
l例如细胞状态可能包含当前主语的性别，因此正确的代词可以被选择出来。当我们看到新的主语，我们希望忘记旧的主语。

image-20200913182224477

第二步——输入

下一步是确定什么样的新信息被存放在细胞状态中。这里包含两个部分。

第一，sigmoid 层称 “输入门层” 决定什么值我们将要更新。

然后，一个 tanh 层创建一个新的候选值向量(这里的输入并不是直接的输入，也是与\(h_{t-1}\)进行了融合)，\(\tilde{C}_t\)，会被加入到状态中。第三步则是这两个信息来产生对状态的更新。
在我们语言模型的例子中，我们希望增加新的主语的性别到细胞状态中，来替代旧的需要忘记的主语。

image-20200913182636802

第一步与第二步的数据相加

image-20200913183849476

第三步——输出

现在是更新旧细胞状态的时间了，\(C_{t-1}\)更新为\(C_t\)。前面的步骤已经决定了将会做什么，我们现在就是实际去完成。
我们把旧状态与\(f_t\)相乘，丢弃掉我们确定需要丢弃的信息。接着加上\(i_t * \tilde{C}_t\)。这就是新的候选值，根据我们决定更新每个状态的程度进行变化。
在语言模型的例子中，这就是我们实际根据前面确定的目标，丢弃旧代词的性别信息并添加新的信息的地方。

image-20200913182821602

三步公式汇总

image-20200913184843663

解决梯度离散问题

由于LSTM有三道门，梯度信息存在相加的情况，所有梯度不会一致出现特别小或者特别大的情况，有效地避免了\(w_{hh}^k\)地情形

参考：https://zhuanlan.zhihu.com/p/30844905

https://www.cnblogs.com/wangduo/p/6773601.html

posted @ 2020-09-13 20:11  Jason66661010  阅读(202)  评论(0)  编辑  收藏  举报