P3884 [JLOI2009]二叉树问题 【离线tarjan或数的向上遍历】

题目

https://www.luogu.com.cn/problem/P3884

 

 

 

 

 

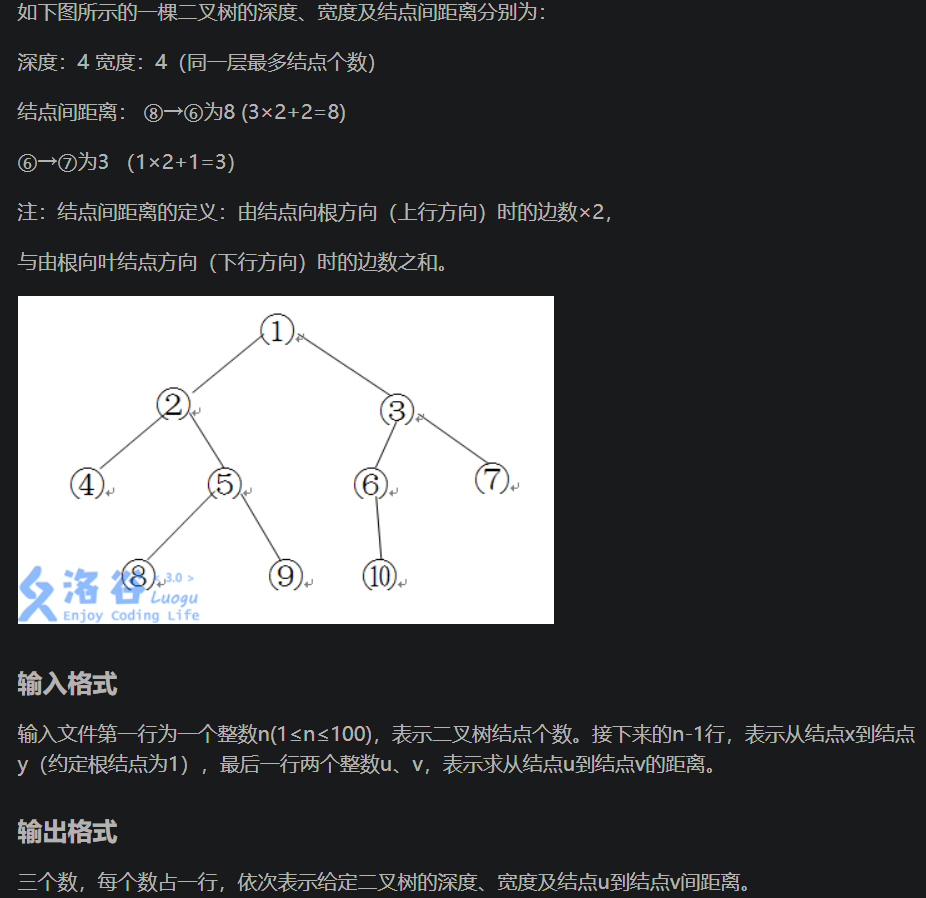
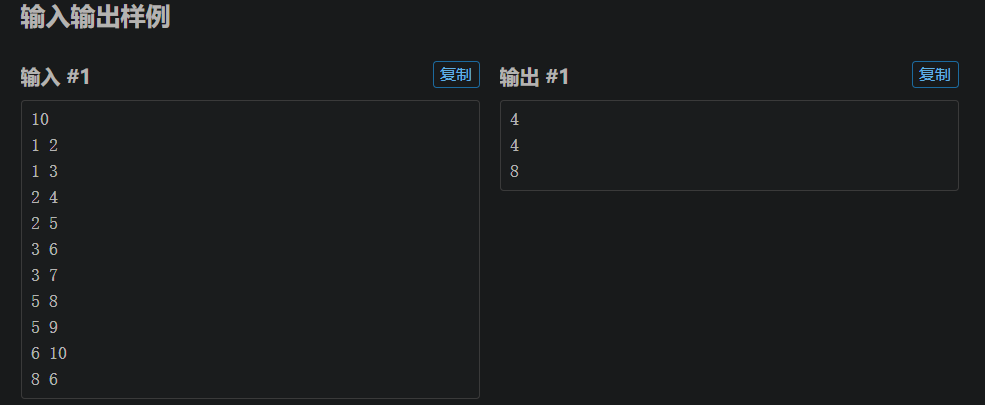
 分析

二叉树的深度、宽度：我们可以使用链式前向星在进行dfs遍历的时候为节点的深度赋值，同时对记录深度的数组的个数加一最后选择深度的最大值，宽度的最大值

U 到V的距离：这里一般的算法就是使用LCA来寻找这两个节点的共同公共祖先，通过公共祖先的路径就是二者的最短路径

于是我们可以使用离线的tarjan算法寻找公共祖先，但是本题的特殊性是题目的图是一个有根树而不是一个无根树，所以我们可以通过记录每一个节点的父亲来寻找公共祖先

方法一

#include<iostream>
#include<cstdio>
using namespace std;
int deep[200], amount[200],head[200],head2[200],vis[200],father[200],answer[200];
int n,cnt=0,cnt2=0;
#define maxn 200
#define maxm 4000
struct edge
{
    int to;
    int next;
}e[maxm*2];
struct edge2
{
    int to;
    int next;
    int num;
}e2[maxm * 2];

void addedge(int u,int v)
{
    cnt++;
    e[cnt].to = v;
    e[cnt].next = head[u];
    head[u] = cnt;
}
void addedge2(int u, int v,int w)
{
    cnt2++;
    e2[cnt2].to = v;
    e2[cnt2].num = w;
    e2[cnt2].next = head2[u];
    head2[u] = cnt2;
}

int maxdepth = -1, maxwidth = -1;
void dfs(int p, int fa,int depth)
{
    deep[p] = depth;
    if (depth > maxdepth)maxdepth = depth;
    amount[depth]++;
    if (amount[depth] > maxwidth)maxwidth = amount[depth];
    for (int i = head[p]; i; i = e[i].next)
    {
        int y = e[i].to;
        if (y == fa)continue;
        dfs(y, p, depth + 1);
    }
}
int find(int x)
{
    if (father[x] == x)return x;
    return father[x] = find(father[x]);
}

void tarjan(int root)
{
    vis[root] = 1;
    for (int i = head[root]; i; i = e[i].next)
    {
        int y = e[i].to;
        if (vis[y])continue;
        
        tarjan(y);
        father[y] = root;
    }
    for (int i = head2[root]; i; i = e2[i].next)
    {
        int y = e2[i].to;
        if (vis[y])answer[e2[i].num] = find(y);
    }
}


int main()
{
    scanf("%d", &n);
    for (int i = 0; i < n - 1; i++)
    {
        int a, b;
        scanf("%d%d", &a, &b);
        addedge(a, b);
        addedge(b, a);
    }
    dfs(1, 0, 1);
    int u, v;
    scanf("%d%d", &u, &v);
    addedge2(u,v,0);
    addedge2(v, u, 0);

    for (int i = 0; i <= n; i++)father[i] = i;
    tarjan(1);
    printf("%d\n", maxdepth);
    printf("%d\n", maxwidth);
    printf("%d", (deep[u]-deep[answer[0]]) * 2 + deep[v]-deep[answer[0]]);
}

方法二

#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
int deep[200], amount[200],head[200],  father[200];
int n, cnt = 0;
#define maxn 200
#define maxm 4000
struct edge
{
    int to;
    int next;
}e[maxm * 2];

void addedge(int u, int v)
{
    cnt++;
    e[cnt].to = v;
    e[cnt].next = head[u];
    head[u] = cnt;
}

int maxdepth = -1, maxwidth = -1;
void dfs(int p, int fa, int depth)
{
    father[p] = fa;
    deep[p] = depth;
    if (depth > maxdepth)maxdepth = depth;
    amount[depth]++;
    if (amount[depth] > maxwidth)maxwidth = amount[depth];
    for (int i = head[p]; i; i = e[i].next)
    {
        int y = e[i].to;
        if (y == fa)continue;
        dfs(y, p, depth + 1);
    }
}


int main()
{
    scanf("%d", &n);
    for (int i = 0; i < n - 1; i++)
    {
        int a, b;
        scanf("%d%d", &a, &b);
        addedge(a, b);
        addedge(b, a);
    }
    dfs(1, 0, 1);
    int u, v;
    scanf("%d%d", &u, &v);
    printf("%d\n", maxdepth);
    printf("%d\n", maxwidth);
    int uu = u, vv = v;
    while (deep[u]!=deep[v])
    {

        if (deep[u] > deep[v]) {  u = father[u]; }
        else { v = father[v]; }
    }
    if (u == v) {
        if (deep[uu] < deep[vv])printf("%d", abs(deep[uu] - deep[vv]));
        else printf("%d", abs(deep[vv] - deep[uu]) * 2);
        return 0; 
    }
    while (father[u] != father[v])
    {
        u = father[u];
        v = father[v];
    }

    
    printf("%d", (deep[uu] - deep[father[u]]) * 2 + deep[vv] - deep[father[u]]);
}

第二种的方法注意要区别两个节点在同一侧还是在不同的两侧