树的重心

定义

对于一颗n个节点的无根树，找到一个点，使得把树变成以该节点为根的有根树时，最大节点数最少。换句话说，删除这个节点后最大连通块（一定是树）的节点数最少。

分析

该问题跟树的最大独立集问题类似。先任选一个节点作为根，把无根树变成有根树，然后设d[i]表示以i为跟的子树的节点个数。只需要一次DFS。

那么删除节点i后，最大连通块有多少节点呢？

节点i的子树中最大的有max(dp[j])【与该节点相连的连通块中节点数选最大的】,i父亲那一块有n-dp[i]个节点。那么其最大子树的节点数就是max(max(dp[j]), n - dp[i])【是自己的父亲上面的连通块大还是自己下面的子树的连通块大】

习题

https://www.luogu.com.cn/problem/P1395

 

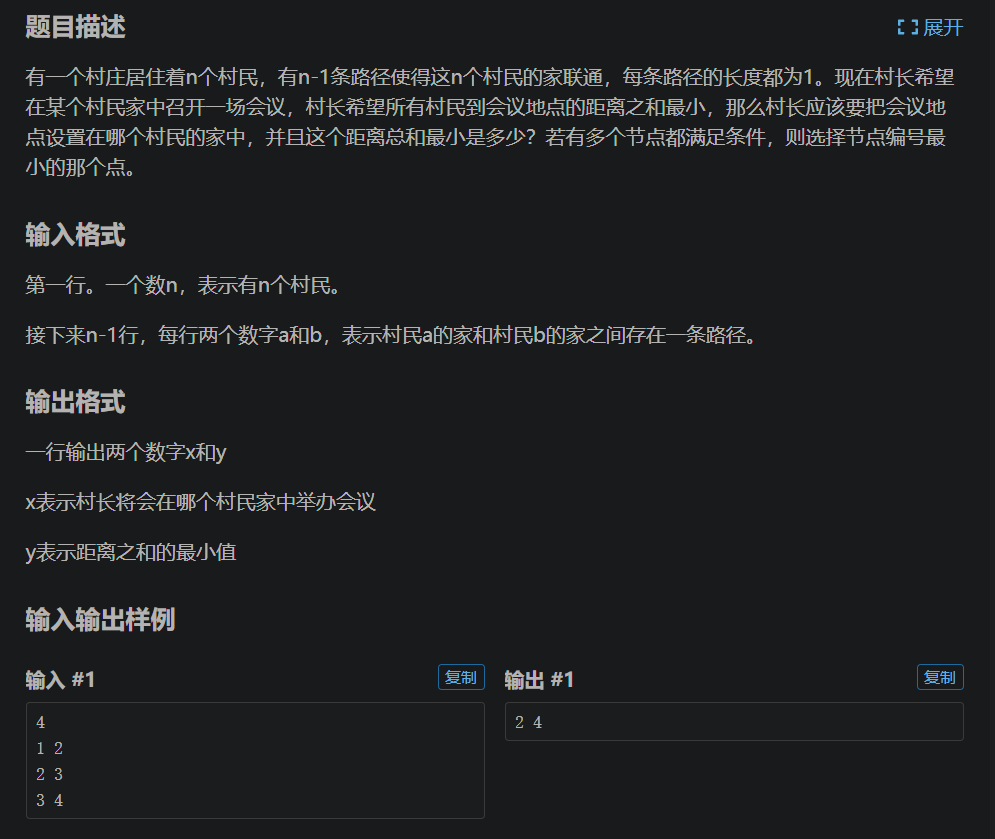
 思路

开始的时候我的思路就是使用简单的floyd算法算出每个点到除自己外每个点的距离，之后相加去最小值，但是肯定超时+爆内存

之后使用上面的树的重心思想，求出该树的重心之后使用BFS计算从该点到其它点的距离

代码

#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<queue>
using namespace std;
#define inf 0x3f3f3f3f
struct node
{
    int to;
    int next;
}e[50001*2];
int n,num[50001],f[50001],cnt=0,head[50001],vis[50001],dis[50001];
void addedge(int  u, int v)
{
    cnt++;
    e[cnt].to = v;
    e[cnt].next = head[u];
    head[u] = cnt;
}
void dfs(int p, int fa)
{
    num[p] = 1;
    for (int i = head[p]; i; i = e[i].next)
    {
        int y = e[i].to;
        if (y == fa)continue;
        dfs(y, p);
        f[p] = max(f[p], num[y]);//求出与该点相连的连通块的节点个数的最大值
        num[p] += num[y];
    }
    f[p] = max(f[p], n - num[p]);//比较是自己父亲的连通块节点个数大还是自己的子树中最大的那个大

}

int main()
{
    scanf("%d", &n);

    for (int i = 0; i < n - 1; i++)
    {
        int a, b;
        scanf("%d%d", &a, &b);
        addedge(a, b);
        addedge(b, a);
    }
    dfs(1, 0);
    int minn=inf, mini = 0;
    for (int i = 1; i <= n; i++)
        if (f[i] < minn)//最后找出最小值
        {
            minn = f[i];
            mini = i;
        }
    queue<int>qq;
    int sum = 0;
    qq.push(mini);
    while (!qq.empty())
    {
        int temp = qq.front(); qq.pop();
        vis[temp]=1;
        sum += dis[temp];
        for (int i = head[temp]; i; i = e[i].next)
        {
            int y = e[i].to;
            if (!vis[y])
            {
                qq.push(y);
                dis[y] = dis[temp] + 1;
            }
        }
    }
    printf("%d %d", mini, sum);  //完美输出
}