P3379 【模板】最近公共祖先（LCA）【tarjan/倍增】

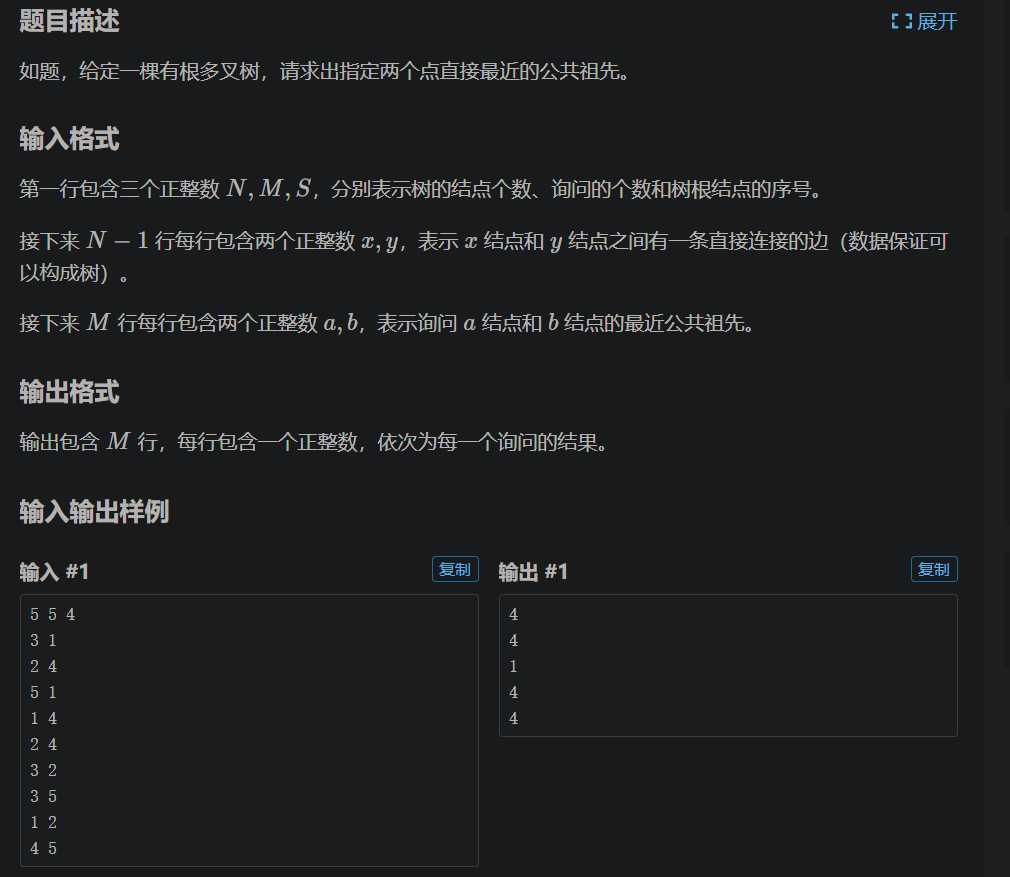
题目

https://www.luogu.com.cn/problem/P3379

 

 

 分析

方法一：tarjan算法

Tarjan算法的基本思路：

　　　1.任选一个点为根节点，从根节点开始。

　　　2.遍历该点u所有子节点v，并标记这些子节点v已被访问过。

　　　3.若是v还有子节点，返回2（递归），否则下一步。

　　　4.合并v到u上。

　　　5.寻找与当前点u有询问关系的点v（从查询的输入中查找）。

　　　6.若是v已经被访问过了，则可以确认u和v的最近公共祖先为v被合并到的父亲节点a。

遍历的话需要用到dfs来遍历(我相信来看的人都懂吧...)，至于合并，最优化的方式就是利用并查集来合并两个节点。

2.模拟过程

假设我们有一组数据 9个节点 8条边 联通情况如下：

　　　　1--2，1--3，2--4，2--5，3--6，5--7，5--8，7--9 即下图所示的树

　　　　设我们要查找最近公共祖先的点为9--8，4--6，7--5，5--3；

　　　　设f[]数组为并查集的父亲节点数组，初始化f[i]=i，vis[]数组为是否访问过的数组，初始为0;　

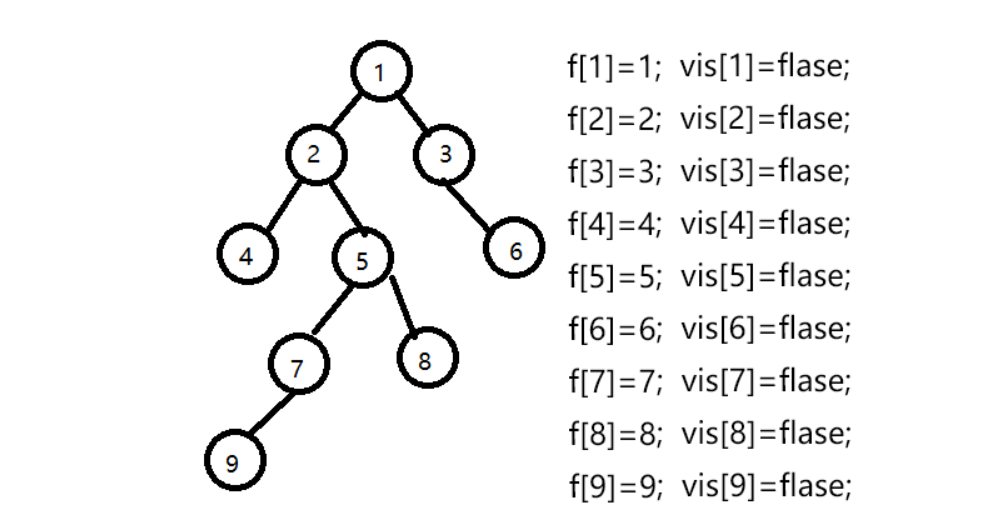
　　　　下面开始模拟过程：

　　　　取1为根节点，往下搜索发现有两个儿子2和3；

　　　　先搜2，发现2有两个儿子4和5，先搜索4，发现4没有子节点，则寻找与其有关系的点；

　　　　发现6与4有关系，但是vis[6]=0，即6还没被搜过，所以不操作；

　　　　发现没有和4有询问关系的点（在所有的测试集合中找有4的测试对，其实就是将所有的测试对都记录下一起测试以节省时间不用测一次找一次，这就是所说的离线形式）了，返回此前一次搜索，更新vis[4]=1；

　　　　

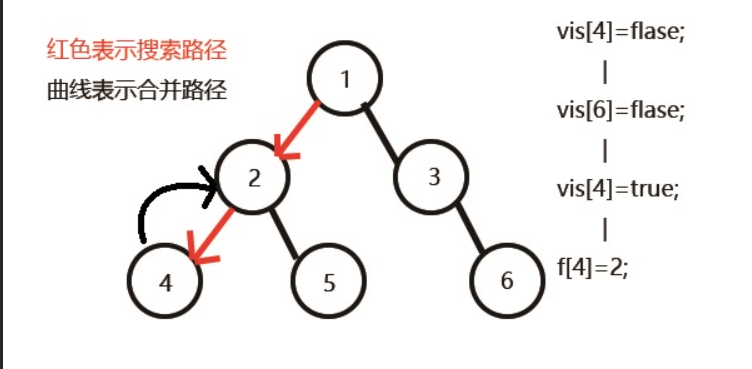
　　　　表示4已经被搜完，更新f[4]=2，继续搜5，发现5有两个儿子7和8;

　　　　先搜7，发现7有一个子节点9，搜索9，发现没有子节点，寻找与其有关系的点；

　　　　发现8和9有关系，但是vis[8]=0,即8没被搜到过，所以不操作；

　　　　发现没有和9有询问关系的点了，返回此前一次搜索，更新vis[9]=1；

　　　　表示9已经被搜完，更新f[9]=7，发现7没有没被搜过的子节点了，寻找与其有关系的点；

　　　　发现5和7有关系，但是vis[5]=0，所以不操作；

　　　　发现没有和7有关系的点了，返回此前一次搜索，更新vis[7]=1；

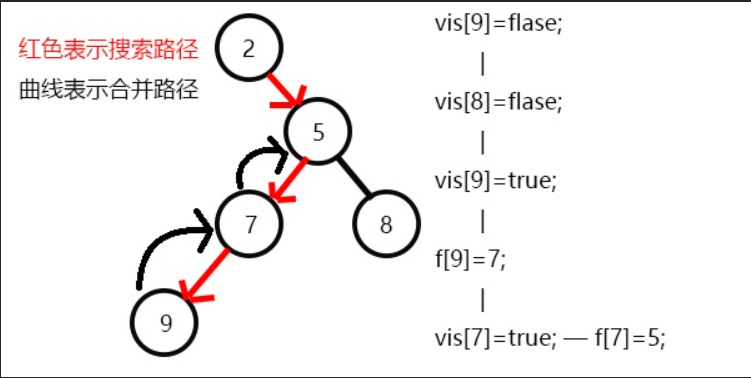
　　　　表示7已经被搜完，更新f[7]=5，继续搜8，发现8没有子节点，则寻找与其有关系的点；

　　　　发现9与8有关系，此时vis[9]=1，则他们的最近公共祖先为find(9)=5；

　　　　　　(find(9)的顺序为f[9]=7-->f[7]=5-->f[5]=5 return 5;并查集)

　　　　发现没有与8有关系的点了，返回此前一次搜索，更新vis[8]=1；

 

　　　　表示8已经被搜完，更新f[8]=5，发现5没有没搜过的子节点了，寻找与其有关系的点；

　　　　

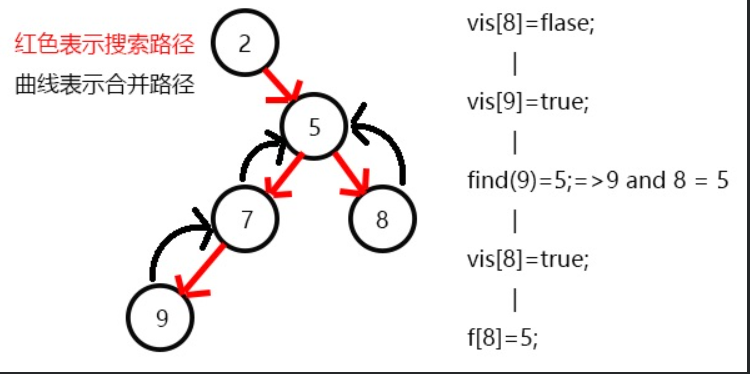
　　　　发现7和5有关系，此时vis[7]=1，所以他们的最近公共祖先为find(7)=5；

　　　　　　(find(7)的顺序为f[7]=5-->f[5]=5 return 5;)

　　　　又发现5和3有关系，但是vis[3]=0，所以不操作，此时5的子节点全部搜完了；

　　　　返回此前一次搜索，更新vis[5]=1，表示5已经被搜完，更新f[5]=2；

　　　　发现2没有未被搜完的子节点，寻找与其有关系的点；

　　　　又发现没有和2有关系的点，则此前一次搜索，更新vis[2]=1；

　　　　

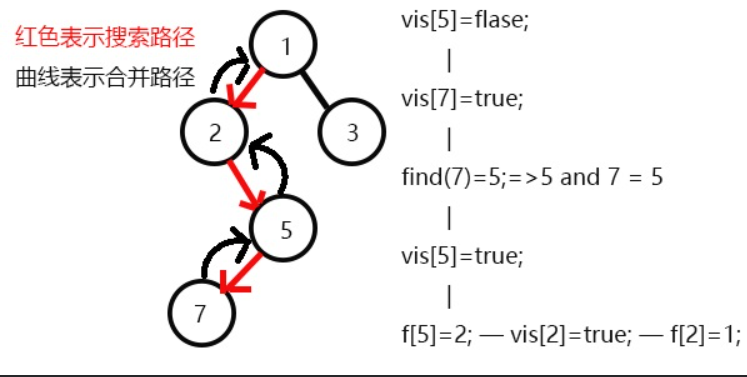
　　　　表示2已经被搜完，更新f[2]=1，继续搜3，发现3有一个子节点6；

　　　　搜索6，发现6没有子节点，则寻找与6有关系的点，发现4和6有关系；

　　　　此时vis[4]=1，所以它们的最近公共祖先为find(4)=1;

　　　　　　(find(4)的顺序为f[4]=2-->f[2]=2-->f[1]=1 return 1;)

　　　　发现没有与6有关系的点了，返回此前一次搜索，更新vis[6]=1，表示6已经被搜完了；

　　　　

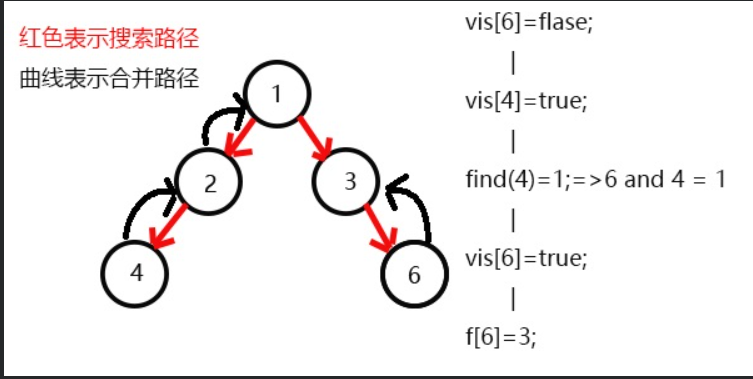
　　　　更新f[6]=3，发现3没有没被搜过的子节点了，则寻找与3有关系的点；

　　　　发现5和3有关系，此时vis[5]=1，则它们的最近公共祖先为find(5)=1；

　　　　　　(find(5)的顺序为f[5]=2-->f[2]=1-->f[1]=1 return 1;)

　　　　发现没有和3有关系的点了，返回此前一次搜索，更新vis[3]=1；

　　　　

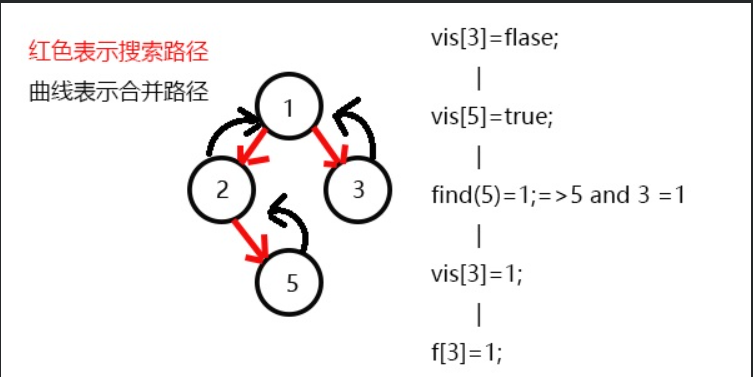
　　　　更新f[3]=1，发现1没有被搜过的子节点也没有有关系的点，此时可以退出整个dfs了。

代码

#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
#include<vector>
using namespace std;
struct node
{
    int to;
    int next;
}e[500001*2];//注意双向图要*2
struct node2
{
    int to;
    int next;
    int num;
}list[500001*2];//注意双向图要*2

int father[500001];//并查集要使用的父亲数组
int visited[500001],head[500001],head2[500001],answer[500001];//answer【i】：第i组查询的lca答案记录
int cnt = 0, cnt2=0,n, m, s;
int find(int x)//并查集的查找
{
    if (father[x] == x)
        return x;
    return father[x] = find(father[x]);
}
void  addedge(int u, int v)
{
    cnt++;
    e[cnt].to = v;
    e[cnt].next = head[u];
    head[u] = cnt;
}
void addedge2(int u, int v,int num)
{
    cnt2++;
    list[cnt2].to = v;
    list[cnt2].num = num;//这里注意：记录了是第几组查询数据
    list[cnt2].next = head2[u];
    head2[u]=cnt2;
}
void tarjan(int root)
{
    father[root] = root;//作为当前的根节点,将其父亲指向自己
    visited[root] = true;
    for (int i = head[root]; i; i = e[i].next)
    {
        int y = e[i].to;
        if (!visited[y])
        {
            tarjan(y);//递归 
            father[y] = root;//更新子节点的父亲
        }
    }
    for (int i = head2[root]; i; i = list[i].next)
    {
        int y = list[i].to;
        if (visited[y])//如果已经查询过，就find输出
            answer[list[i].num] = find(y);
    }
}

int main()
{
    scanf("%d%d%d", &n, &m, &s);
    for (int i = 0; i < n - 1; i++)
    {
        int a, b;
        scanf("%d%d", &a, &b);
        addedge(a, b);
        addedge(b,a);
    }
    for (int i = 1; i <= n; i++)
        father[i] = i;//首先将所有节点的父亲节点指向自己
    for (int i = 0; i < m; i++)
    {
        int a, b;
        scanf("%d%d", &a, &b);
        addedge2(a, b, i);
        addedge2(b, a, i);
    }
    tarjan(s);
    for (int i = 0; i < m; i++)
        printf("%d\n", answer[i]);
}

法二：倍增方法（自己不太熟悉）

#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
using namespace std;
struct node
{
    int to;
    int next;
}e[500001*2];//注意双向图要*2
int father[500001][22];
//fa[i][k]表示节点i的上2^k层的祖先是哪个点
/*为什么不直接让fa[i][k]表示节点i的上k层的祖先是哪个点？
1.空间N*N会炸
2.每次遇到一个点都要往上爬看他的祖先，时间复杂度巨大。如果这棵树长得像一条链，那时间复杂度为
0+1+2+……+(n-1)=n(n-1)/2
*/
int visited[500001], head[500001], depth[500001], lg[500001];
int cnt = 0, cnt2=0,n, m, s;
void dfs(int now,int fa)  //例如u的上4层祖先为上2层祖先的上2层祖先
{
    father[now][0] = fa;
    depth[now] = depth[fa] + 1;
    for (int i = 1; i <= lg[depth[now]]; i++)
        father[now][i] = father[father[now][i - 1]][i - 1];
    for (int i = head[now]; i; i = e[i].next)
    {
        int y = e[i].to;
        if(y!=fa)
        dfs(y, now);
    }
}
void  addedge(int u, int v)
{
    cnt++;
    e[cnt].to = v;
    e[cnt].next = head[u];
    head[u] = cnt;
}
int  lca(int x,int y)
{
    if (depth[x] < depth[y]) swap(x, y);
    while (depth[x] > depth[y])
        x = father[x][lg[depth[x] - depth[y]] - 1];
    //lg[dep[x]-dep[y]]表示log(dep[x]-dep[y])+1,再减去1 
    //让x往上跳2^log([dep[x]-dep[y])层
    /*这里就要用到lg数组判断x要往上跳多少
        Q1：为什么要一步一步以2的k次方跳跃？
        因为fa[x][k]表示的是x的2^N层上的祖先, 所以不能一步跳到上k（k为任意数）层的
        让x往上跳(2 ^ k1 + 2 ^ k2 + 2 ^ k3 + ......)层 才能让x和y达到同一高度
        Q2：为什么x可以一步一步跳上y那一层？
        设 k = log([dep[x] - dep[y])
        k是向下取整，例如dep[x] - dep[y] = 5 = (101)2 = (100)2 + (1)2（二进制表示）
        那么就要往上跳2次，分别跳(100)2 、(1)2 层
        （所以，log(x)也可以表示x二进制除了最高位的1之外都去掉的形式）
        往上跳了一次以后，dep[x] - dep[y] = (101)2 - (100)2 = (1)2，再往上跳(1)2层就可以了
        x一步一步逼近y那一层，dep[x] - dep[y]一步一步减小，就能达到了
        */
    if (x == y) return x;
    for (int k = lg[depth[x]] - 1; k >= 0; --k)
        if (father[x][k] != father[y][k])
            x = father[x][k], y = father[y][k];
    //注意:层数=......,8,4,2,1 设p=2^k
    //如果`x的上p层的祖先的爸爸还是和`y的上p层的祖先的爸爸不一致
    //那么就让ta们往上爬p层
    return father[x][0];
}
int main()
{
    scanf("%d%d%d", &n, &m, &s);
    for (int i = 0; i < n - 1; i++)
    {
        int a, b;
        scanf("%d%d", &a, &b);
        addedge(a, b);
        addedge(b,a);
    }
    for (int i = 1; i <= n; ++i)
        lg[i] = lg[i - 1] + (1 << lg[i - 1] == i);
    dfs(s, 0);
    for (int i = 0; i < m; i++)
    {
        int a, b;
        scanf("%d%d", &a, &b);
        printf("%d\n", lca(a,b));
    }
    
}