P1462 通往奥格瑞玛的道路【最大值中的最小】

题目

https://www.luogu.com.cn/problem/P1462

题目背景

在艾泽拉斯大陆上有一位名叫歪嘴哦的神奇术士，他是部落的中坚力量

有一天他醒来后发现自己居然到了联盟的主城暴风城

在被众多联盟的士兵攻击后，他决定逃回自己的家乡奥格瑞玛

题目描述

在艾泽拉斯，有n个城市。编号为1,2,3,...,n。

城市之间有m条双向的公路，连接着两个城市，从某个城市到另一个城市，会遭到联盟的攻击，进而损失一定的血量。

每次经过一个城市，都会被收取一定的过路费（包括起点和终点）。路上并没有收费站。

假设1为暴风城，n为奥格瑞玛，而他的血量最多为b，出发时他的血量是满的。

歪嘴哦不希望花很多钱，他想知道，在可以到达奥格瑞玛的情况下，他所经过的所有城市中最多的一次收取的费用的最小值是多少。

输入格式

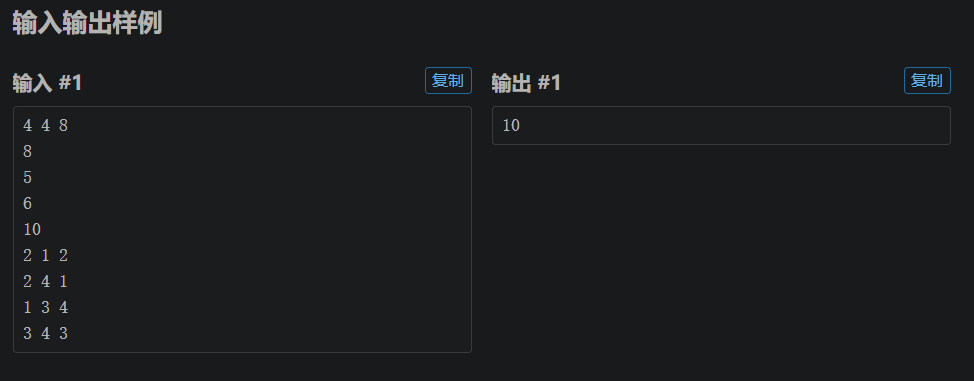
第一行3个正整数，n，m，b。分别表示有n个城市，m条公路，歪嘴哦的血量为b。

接下来有n行，每行1个正整数，fi。表示经过城市i，需要交费fi元。

再接下来有m行，每行3个正整数，ai，bi，ci(1<=ai，bi<=n)。表示城市ai和城市bi之间有一条公路，如果从城市ai到城市bi，或者从城市bi到城市ai，会损失ci的血量。

输出格式

仅一个整数，表示歪嘴哦交费最多的一次的最小值。

如果他无法到达奥格瑞玛，输出AFK。

 

 分析

这个题极其的……

他所经过的所有城市中最多的一次收取的费用的最小值是多少：翻译如下：

他可能有多条路径能够回城，那么求的就是这些路径中的每一条路径 经过的城市中收费最多的数字，现在要求这个数字最小可以是多少

思路

至于在路上他的血够不够，我们可以将路上失去的血量视为路径的长度，然后使用Dijkstra来判断他的血够不够回城

接下来的问题就是寻找最小值的问题了

具体的思路就是我们设置一个花费最大值变量cost，它必须是一条可行路径上费用最大的值，该路径上节点的费用必须比它小

在使用Dijkstra判断血够不够的同时来判断该路径上有没有节点的费用比cost大，有的话说明我们自己设得这个cost值偏大，于是把cost改小一点继续。

这样一来初步得思路就是我们让cost从1遍历到所有节点费用的最大值，一旦不存在节点的费用比cost大，那么此时的cost就是多条可行路径中经过城市中收费最多的数字里最小的一个，也就是最终的答案

但是cost从1遍历到所有节点费用的最大值，每遍都要执行一次Dijkstra，可能会超时，所以我们使用二分搜索，来加快cost的确定速度

代码

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<string>
#include<cstring>
#include<queue>
#define inf 0x3f3f3f3f 
#define maxn 10001
#define maxm 50001
using namespace std;
struct edge
{
    int to;
    int dis;
    int next;
}e[maxm*2];
struct node
{
    int dis;
    int pos;
    bool operator<(const node &x)const
    {
        return dis > x.dis;
    }
};
int n, m, b;
int bb[maxn], cc[maxn], head[maxn], dis[maxn], vis[maxn], cnt = 0;
void addedge(int u, int v, int  w)
{
    cnt++;
    e[cnt].dis = w;
    e[cnt].to = v;
    e[cnt].next = head[u];
    head[u] = cnt;
}
int check(int cost)
{
    if (cost < bb[1]||cost<bb[n])return 0;//由于是从起点出发，到终点结束，如果cost一开始就比这两个点的费用小，那么cost就不是该路径中收费最多的，直接返回false
    memset(dis, inf, sizeof(dis));
    memset(vis, 0, sizeof(vis));
    dis[1] = 0;
    /*for (long long i = 1; i <= n; i++)
        if (bb[i]>cost)vis[i] = true;
        else vis[i] = false;*/
    priority_queue<node>q;
    q.push({0,1});
    while (!q.empty())
    {
        int x = q.top().pos; q.pop();
        if (vis[x])continue;
        vis[x] = 1;
        for (int i = head[x]; i; i = e[i].next)
        {
            int y = e[i].to;
            if (bb[y]>cost)continue;//因为下面的if是使用节点x作为中转节点来更新起点s到其它点（y）的距离的，所以要判断y点的费用是不是比cost小（保证cost的费用是在最大的）
            if (dis[y]>dis[x] + e[i].dis)
            {
                dis[y] = dis[x] + e[i].dis;
                q.push({ dis[y],y });        
            }
        }
    }
    if (dis[n] <= b)return 1;//当该条路径完毕后，看看需要的最小血量与人拥有的血量大小关系，判断能不能活着回去
    else return 0;
}

int main()
{
    scanf("%d%d%d", &n, &m, &b);
    for (int i = 1; i <= n; i++)
    {
        scanf("%d", &bb[i]);
        cc[i] = bb[i];
    }
    sort(cc + 1, cc + n + 1);//二分要排序
    for (int i = 0; i < m; i++)
    {
        int ta, tb, tc;
        scanf("%d%d%d", &ta, &tb, &tc);
        addedge(ta, tb, tc);
        addedge(tb, ta, tc);
    }
    int l = 1, r = n, mid;
    int ans = -1;
    while (l <= r)
    {
        mid = (l + r) / 2;
        if (check(cc[mid]))
        {
            ans = cc[mid];
            r = mid - 1;
        }
        else l = mid + 1;
    }
    if (ans == -1)printf("AFK\n");
    else printf("%lld", ans);

}