编辑距离

编辑距离

编辑距离（Edit Distance），又称Levenshtein距离，是指两个字串之间，由一个转成另一个所需的最少编辑操作次数。许可的编辑操作包括将一个字符替换成另一个字符，插入一个字符，删除一个字符。一般来说，编辑距离越小，两个串的相似度越大。

其中的字符操作包括：

删除一个字符     a) Insert a character

插入一个字符     b) Delete a character

修改一个字符     c) Replace a character

问题

给定两个字符串A和B，求字符串A至少经过多少步字符操作变成字符串B。 

分析

（假设让字符串A变为B）首先，如果字符串A的长度为0，则A变为B的编辑距离就是B此时的长度（可以理解为向A添加B的每一位字符）：得出

for (int j = 0; j <= tlen; j++)
　　edit[0][j] = j;

同理如果字符串B的长度为0，则A变为B的编辑距离就是A此时的长度（可以理解为A删除自己的每一位字符）得出：

for (int i = 0; i <=slen; i++)
edit[i][0] = i;

接下来考虑A串的第i个字符和B串的第j个字符。

如果A串的第i个字符和B串的第j个字符相等，即A[i]=B[j]，则只需要计算A[i...lenA]和B[j...lenB]之间的距离即可。如果不相等，则：

1修改A串的第i个字符成B串的第j个字符，之后仅需要计算A[i+1...lenA]和B[j+1...lenB]的距离即可；

2删除A串的第i个字符，之后仅需要计算A[i+1...lenA]和B[j...lenB]的距离即可；

3把B串的第j个字符插入到A串的第i个字符之前，之后仅需要计算A[i...lenA]和B[j+1...lenB]的距离即可。

动态规划方程

 

 例题

https://www.luogu.com.cn/problem/P2758

 

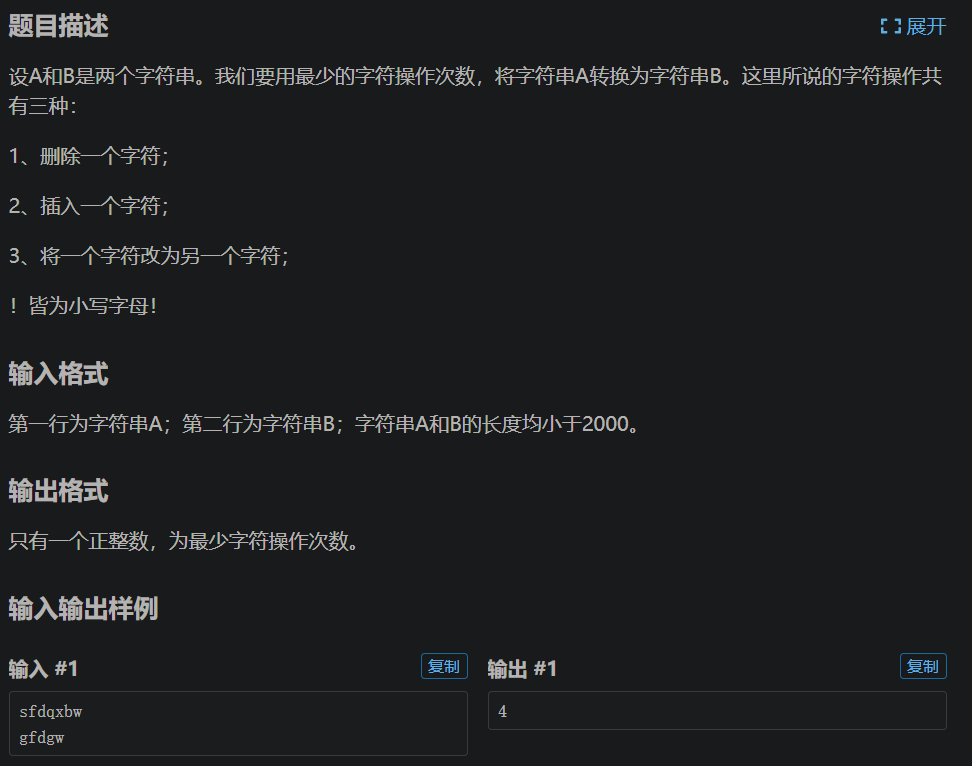
 代码

#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
#include<algorithm>
using namespace std;
string s, t;
int slen = 0, tlen = 0;
int edit[2002][2002];//动态规划数组是从1开始的记录字符的
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    cin >> s;
    cin >> t;
    slen = s.length(); tlen = t.length();
    for (int i = 0; i <=slen; i++)//初始化
        edit[i][0] = i;
    for (int j = 0; j <= tlen; j++)//初始化
        edit[0][j] = j;
    for (int i = 1; i <= slen; i++)
    {
        for (int j = 1; j <=tlen; j++)
        {
            edit[i][j] = min(edit[i - 1][j]+1, edit[i][j - 1]+1);
            edit[i][j] = min(edit[i][j],edit[i-1][j-1]+(s[i-1]!=t[j-1]));
            //这里是比较三种编辑方法哪种能让此时的edit[i][j]变得最小。（假设是A变为B）
            //首先是edit[i - 1][j]+1：可以理解为在A串长度为i-1,b串长度为j的情况下，向A添加一个字符变为edit[i][j]
            //接着是edit[i][j - 1]+1：可以理解为在A串长度为i,b串长度为j-1的情况下，A删除一个字符变为edit[i][j]
            //最后是edit[i-1][j-1]+(s[i-1]!=t[j-1])：可以理解为在A串长度为i-1,b串长度为j-1的情况下，看此时A B的字符是否一样，一样直接赋值，不一样再加一
        }
    }
    printf("%d", edit[slen][tlen]);
}

参考：https://blog.csdn.net/cxu123321/article/details/105338085?utm_medium=distribute.pc_relevant.none-task-blog-baidujs-1

https://blog.csdn.net/baodream/article/details/80417695