矩阵快速幂

快速幂

点击这里

矩阵快速幂

最浅显的作用就是用来求一个矩阵的n次幂，就是将快速幂中的数字映射成矩阵

#include<iostream>
#include<algorithm>
#include<cstdio>
using namespace std;
#define N 102
#define mod 1000000007//一般会对结果进行取余
int tmp[N][N],ans[N][N],ori[N][N];//ori是输入的矩阵，ans是承接结果的矩阵，tmp是临时矩阵
void mul(int a[][N],int b[][N], int n)
{
    //fill(tmp[0], tmp[0] + N*N, 0);
    memset(tmp, 0, sizeof tmp);
        for (int i = 0; i < n; i++)//矩阵的乘法
            for (int j = 0; j < n; j++)
                for (int k = 0; k < n; k++)
                tmp[i][j] +=(a[i][k] * b[k][j]%mod)%mod;
    for (int i = 0; i < n; i++)//将tmp矩阵复制到a矩阵
        for (int j = 0; j < n; j++)
            a[i][j] = tmp[i][j];
}

void pow(int a[][N], int power)
{
    memset(ans, 0, sizeof ans);//n是幂，N是矩阵大小
    for (int i = 0; i < N; i++)
        ans[i][i] = 1;//设置为单位矩阵（与快速幂中的result是是一样的作用）
    while (power)//与单个数字的快速幂一样
    {
        if (power & 1)
            mul(ans, a, N);//是奇数就用ans承接结果
        power >>= 1;
        mul(a, a, N);//是偶数就执行a的平方来降幂
    }
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int n,k;
    cin >> n >> k;
    for (int i = 0; i < n; i++)
        for (int j = 0; j < n; j++)
            cin >> ori[i][j];
    pow(ori, k);
    
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < n; j++)
            printf("%s%d", j == 0 ? "" : " ", ans[i][j]);//输出结果
        cout << endl;
    }

}

实用代码

上面的代码只是为了较好地理解矩阵快速幂的算法实现，但是其中涉及到矩阵的复制、较多的初始化，在实际解题中会不适用，故如下给出实用代码

#include<iostream>
#include<algorithm>
#include<cstdio>
using namespace std;
#define N 102
#define mod 1000000007
struct matrix//使用struct
{
    long long c[N][N];
}aa, bb;//注意：在这里初始化的aa、bb矩阵中默认值为0（aa表示初始矩阵，bb表示计算的结果矩阵）
long long ans[N][N], ori[N][N];
long long n, k;
matrix mul(matrix a, matrix b)
{
    matrix tmp;//这里初始化矩阵中的值为随机数，所以要将其设为0（也是为了后续的函数中能够使用tmp而不影响结果）
    for (int i = 0; i < n; i++)
        for (int j = 0; j < n; j++)
            tmp.c[i][j] = 0;

    for (int i = 0; i < n; i++)
        for (int j = 0; j < n; j++)
            for (int k = 0; k < n; k++)
                tmp.c[i][j] = (tmp.c[i][j] + (a.c[i][k] * b.c[k][j]) % mod) % mod;
    return tmp;//直接返回struct结构体，不用矩阵复制
}

matrix pow(long long power)
{
    matrix ans;//这里初始化矩阵中的值为随机数，所以要将其设为0，对角线置为1，表示一个单位矩阵，否则后续结果会出错
    for (int i = 0; i < n; i++)
        for (int j = 0; j < n; j++)
        {
            if (i == j)ans.c[i][j] = 1;
            else ans.c[i][j] = 0;
        }

    while (power)//与单个数字的快速幂一样
    {
        if (power & 1)
            ans = mul(ans, aa);
        power >>= 1;
        aa = mul(aa, aa);
    }
    return ans;
}
int main()
{
    scanf("%lld%lld", &n, &k);
    for (int i = 0; i < n; i++)
        for (int j = 0; j < n; j++)
            scanf("%lld", &aa.c[i][j]);
    bb = pow(k);

    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < n; j++)
            printf("%s%lld", j == 0 ? "" : " ", bb.c[i][j]);
        cout << endl;
    }

}

实用代码优化【模板】

上面代码的单位矩阵是后面新建的，而我们可以直接使用bb作为单位矩阵 给出矩阵快速幂的最后模板

#include<iostream>
#include<algorithm>
#include<cstdio>
using namespace std;
#define N 102
#define mod 1000000007
struct matrix
{
    long long c[N][N];
}aa,bb;
long long ans[N][N], ori[N][N];
long long n, k;
matrix mul(matrix a, matrix b)
{
    matrix tmp;    
    for (int i = 0; i < n; i++)//这里初始化矩阵中的值为随机数，所以要将其设为0（也是为了后续的函数中能够使用tmp而不影响结果）
        for (int j = 0; j < n; j++)
            tmp.c[i][j] = 0;

    for (int i = 0; i < n; i++)
        for (int j = 0; j < n; j++)
            for (int k = 0; k < n; k++)
                tmp.c[i][j] =(tmp.c[i][j]+ (a.c[i][k] * b.c[k][j]) % mod) % mod;//注意这里的取余方式，现在乘法取余，防止在乘法就溢出
    return tmp;//直接返回struct结构体，不用矩阵复制
}

matrix pow(long long power)
{
    for (int i = 0; i < n; i++)
        bb.c[i][i] = 1;//使用bb作为单位矩阵来承接结果
    while (power)//与单个数字的快速幂一样
    {
        if (power & 1)
            bb=mul(bb, aa);
        power >>= 1;
        aa=mul(aa, aa);
    }
    return bb;
}
int main()
{
    scanf("%lld%lld", &n, &k);
    for (int i = 0; i < n; i++)
        for (int j = 0; j < n; j++)
            scanf("%lld",&aa.c[i][j]);
    bb=pow( k);
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < n; j++)
            printf("%s%lld", j == 0 ? "" : " ", bb.c[i][j]);
        cout << endl;
    }
}

简单练习

https://www.luogu.com.cn/problem/P3390（使用模板代码即可解决）

矩阵快速幂的用途

求解递推式的值（就像是高中数学的那种）

例题：https://www.luogu.com.cn/problem/P1939

解题步骤

第一步：列出递推式：ax=ax-1+ax-3(x>3)

第二步：ax最早是由ax-3三而来，而矩阵快速幂所解决的问题范围又是方阵，所以我们构造需要一个3*3的方阵

第三步：推理

这是第n项AN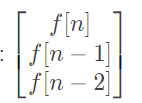：这是第n-1项AN-1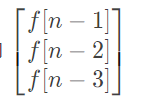：于是我们构造的矩阵ans应该满足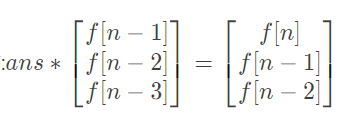

 

将第n-1项横过来：f[n-1]  f[n-2]  f[n-3]  

f[n]= f[n-1]+f[n-3] :      1         0        1  (只需要f[n-1]    f[n-3]  )

 f[n-1]                   :      1         0        0  (第n-1项中有f[n-1]  )

 f[n-2]                   :      0         1        0  (第n-1项中有f[n-2]  )

 于是构造的ans矩阵就出来了

第四步：求解

这样一来就求出一个等比数列：An=ans*An-1——>An=ansn-1*A1(这里的A1就是【1 1 1 】即 初始a1 a2 a3的值)

代码

#include<iostream>
#include<algorithm>
#include<cstdio>
using namespace std;
#define N 102
#define mod 1000000007
struct matrix
{
    long long c[N][N];
}aa, bb;
long long ans[N][N], ori[N][N];
long long n, k;
matrix mul(matrix a, matrix b)
{
    matrix tmp;
    for (int i = 0; i < n; i++)
        for (int j = 0; j < n; j++)
            tmp.c[i][j] = 0;

    for (int i = 0; i < n; i++)
        for (int j = 0; j < n; j++)
            for (int k = 0; k < n; k++)
                tmp.c[i][j] = (tmp.c[i][j] + (a.c[i][k] * b.c[k][j]) % mod) % mod;
    return tmp;
}

matrix pow(long long power)
{
    for (int i = 0; i < n; i++)
        bb.c[i][i] = 1;
    while (power)//与单个数字的快速幂一样
    {
        if (power & 1)
            bb = mul(bb, aa);
        power >>= 1;
        aa = mul(aa, aa);
    }
    return bb;
}
int main()
{
    aa.c[0][0] = aa.c[0][2] = aa.c[1][0] = aa.c[2][1] = 1;//为初始的aa矩阵赋值（就是分析中的ans矩阵）
    n = 3;//矩阵的大小为3
    scanf("%lld",&k);
    for (int i = 0; i < k; i++)
    {
        long long tt;
        scanf("%lld", &tt);
        if (tt <= 3)
        {
            printf("1\n"); continue;
        }
        bb = pow(tt-1);
        printf("%lld\n", bb.c[0][0]);//在An项中，她是一个三行一列的矩阵，而所求的an就是第一行的值
        for (int i = 0; i < n; i++)
        {
            for (int j = 0; j < n; j++)
            {
                bb.c[i][j] = 0; aa.c[i][j] = 0;//因为要求多次，所以要重新初始化aa、bb矩阵
            }
        }
        aa.c[0][0] = aa.c[0][2] = aa.c[1][0] = aa.c[2][1] = 1;
    }

}

 

参考：https://blog.csdn.net/zhangxiaoduoduo/article/details/81807338、https://blog.csdn.net/red_red_red/article/details/90208713、https://www.luogu.com.cn/blog/_post/101179

 
posted @ 2020-05-17 18:49  Jason66661010  阅读(193)  评论(0)  编辑  收藏  举报