Bellman-Ford算法
算法适用
当在图中出现负权的时候，使用Dijkstra算法将不能在正确的求出结果，所以引入Bellman-Ford算法
算法原理
该算法的原理其实就如同Dijkstra算法一样进行边的松弛
松弛一轮后的结果就是初始节点只经过一条边到达其余各个节点的最短路径长度，因为只检测了添加一个点对距离的影响
那么松弛的轮数最多是n-1，因为n个顶点的图最多包含n-1条边，而且有可能在n-1轮松弛之前就已经完成了dis数组的更新不再变化
例如：
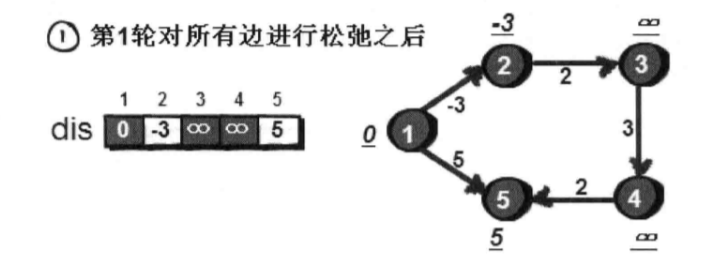
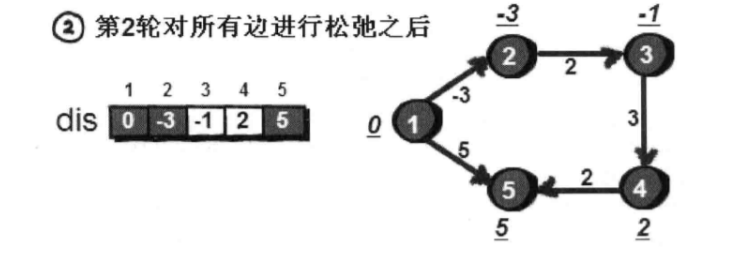
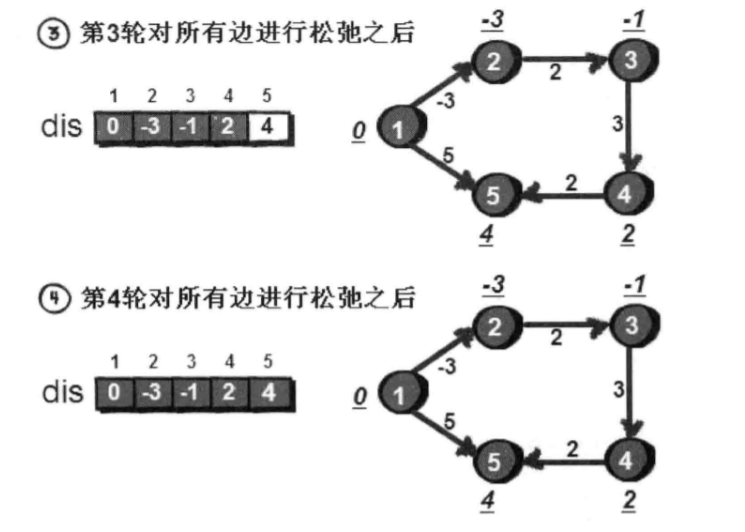
（3 4之间dis未发生变化）
算法核心代码
for (int k = 1; k <=n - 1; k++) for (int i = 1; i <= m; i++) if (dis[v[i]]>dis[u[i]] + w[i]) dis[v[i]] = dis[u[i]] + w[i];//进行n-1次的松弛
算法完整代码
#include<iostream> #include<algorithm> using namespace std; int dis[200], n, m, u[200], v[200], w[200]; #define inf 0x3f3f3f3f int min = inf; int start = 1;//设置起始节点为1号节点 int main() { scanf("%d%d", &n, &m); for (int i = 1; i <=m; i++) scanf("%d%d%d", &u[i], &v[i], &w[i]); fill(dis, dis + 200, inf);//初始化距离数组 dis[start] = 0;//起始节点的距离值设置为0 for (int k = 1; k <=n - 1; k++) for (int i = 1; i <= m; i++) if (dis[v[i]]>dis[u[i]] + w[i]) dis[v[i]] = dis[u[i]] + w[i];//进行n-1次的松弛 //检测负权回路 bool flag = false; for (int i = 1; i <= m; i++) if (dis[v[i]] > dis[u[i]] + w[i])//在进行了n-1次后的松弛后如果还有dis[v[i]] > dis[u[i]] + w[i]就是存在回路 flag = true; for (int i = 1; i <= n; i++) cout << dis[i] << ' '; } //5 5 //2 3 2 //1 2 -3 //1 5 5 //4 5 2 //3 4 3
检测负权回路
算法简单优化
由于算法可能在n-1次松弛之前就完成任务，所以可以设置一个back数组记录dis，如果在迭代之后dis没有变变化就结束松弛
检测负权回路+算法简单优化代码
#include<iostream> #include<algorithm> using namespace std; int dis[200],back[200],n, m, u[200], v[200], w[200]; #define inf 0x3f3f3f3f int min = inf; int main() { scanf("%d%d", &n, &m); for (int i = 1; i <= m; i++) scanf("%d%d%d", &u[i], &v[i], &w[i]); fill(dis, dis + 200, inf); dis[1] = 0; int check = 0; for (int k = 1; k <= n - 1; k++) { for (int i = 1; i <= n; i++)back[i] = dis[i];//使用back数组记录dis数组 for (int i = 1; i <= m; i++) if (dis[v[i]] > dis[u[i]] + w[i]) dis[v[i]] = dis[u[i]] + w[i]; for (int i = 1; i <= n; i++) { if (back[i] != dis[i]) { check = 1; break; }//如果数组未发生变化就直接中断 } if (check == 0)break; } //检测负权回路 bool flag = false; for (int i = 1; i <= m; i++) if (dis[v[i]] > dis[u[i]] + w[i]) flag = true; for (int i = 1; i <= n; i++) cout << dis[i] << ' '; }
邻接表的数组表示方法
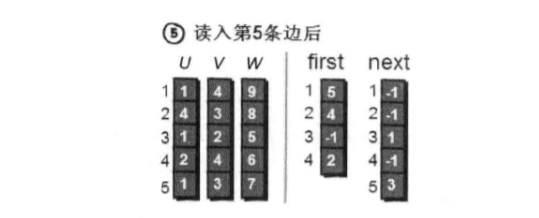
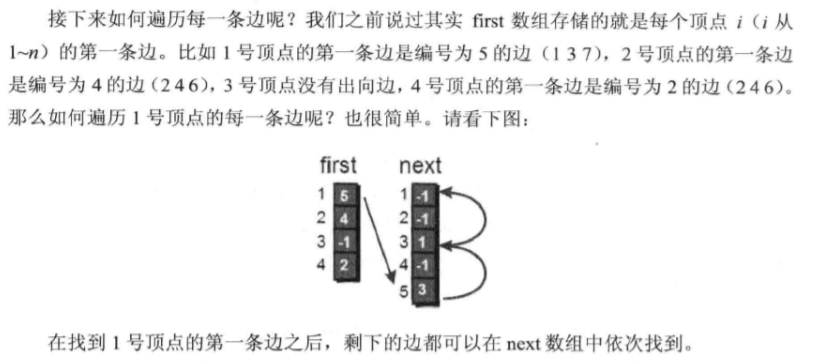
简单总结一下就是first[u[i]]是保存顶点u[i]的第一条边的编号，而next保存编号为i的边的下一条边的编号
算法的队列优化
能满足if (dis[v[k]] > dis[u[k]] + w[k])的k值并且在队列中不存在的值，才会进入队列，这样从队列中取数松弛，才保证每次都进行有效的更新
代码
#include<iostream> #include<algorithm> #include<queue> using namespace std; int dis[200],n, m, u[200], v[200], w[200],first[200],nexts[200],visited[200]; //first[200],nexts[200]分别是邻接表中的数组，visited是用来记录队列中是否存在元素，否则需要一次次遍历寻找 queue<int>que; int start = 1; #define inf 0x3f3f3f3f int min = inf; int main() { scanf("%d%d", &n, &m); fill(dis, dis + 200, inf);//初始化距离数组 dis[start] = 0;//起始节点的距离值设置为0 fill(first, first + n, -1);//first数组以及next数组初始化为-1 fill(nexts, nexts + n, -1); for (int i = 1; i <= m; i++) { scanf("%d%d%d", &u[i], &v[i], &w[i]); //建立邻接表 nexts[i] = first[u[i]]; first[u[i]] = i; } que.push(start);//起点入队 visited[start] = 1; while (!que.empty()) { int k = first[que.front()];//第一条边的编号 while (k != -1) { if (dis[v[k]] > dis[u[k]] + w[k]) { dis[v[k]] = dis[u[k]] + w[k]; if (visited[v[k]] == 0)//如果队中不存在就入队 { que.push(v[k]); visited[v[k]] = 1; } } k = nexts[k];//k变为下一条边的编号 } visited[que.front()] = 0;//出队 que.pop(); } for (int i = 1; i <= n; i++) cout << dis[i] << ' '; }
