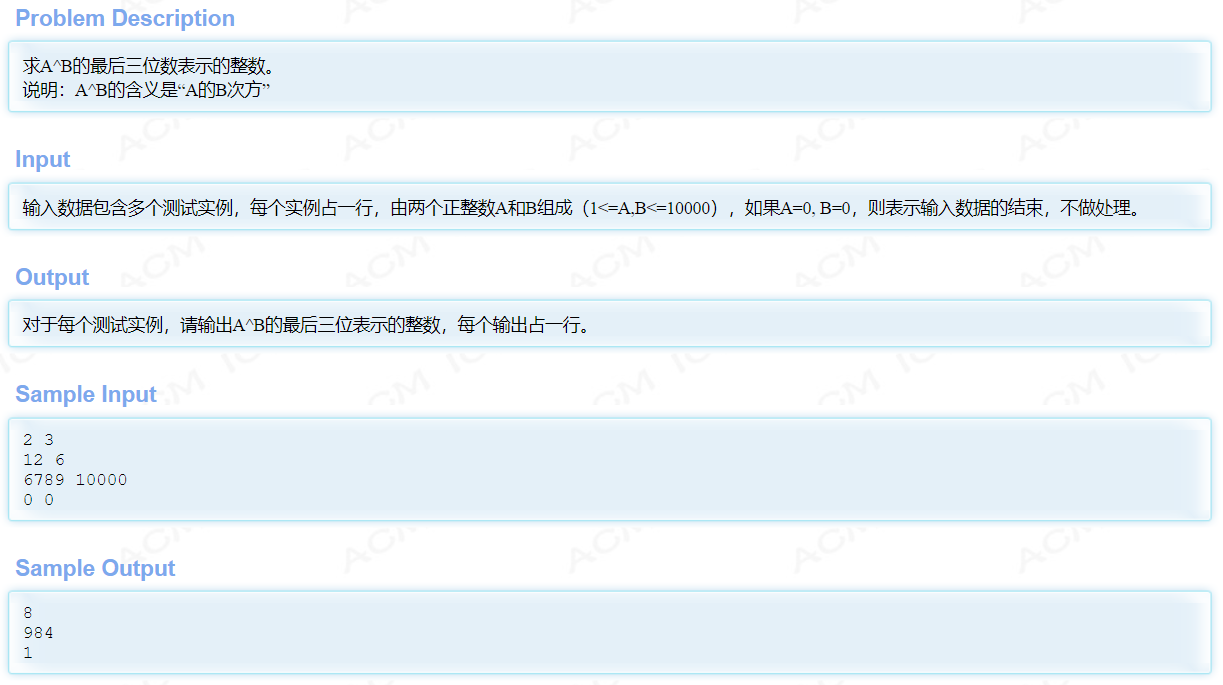
快速幂

能解决的问题类型

http://acm.hdu.edu.cn/showproblem.php?pid=2035

 

 

 

基本方法

#include<iostream>
using namespace std;
int normalPower(int base, int power)
{
    long long result = 1;
    for (int i = 0; i < power; i++)
        result = result*base;
    return result % 1000;
}
int main()
{
    int a, b;
    scanf("%d %d", &a, &b);
    printf("%d", normalPower(a, b));
}

但是6789 10000的结果却是313，显然与答案不符。原因是数字太大，导致溢出。

改进方法

取模的其中一条运算规则就是(a * b) % p = (a % p * b % p) % p

所以我们可以借助这个法则，只需要在循环乘积的每一步都提前进行“取模”运算，而不是等到最后直接对结果“取模”，也能达到同样的效果。

#include<iostream>
using namespace std;
int normalPower(int base, int power)
{
    long long result = 1;
    for (int i = 0; i < power; i++)
    {
        result = result*base;
        result = result % 1000;//这里进行改动
    }
    return result % 1000;
}
int main()
{
    int a, b;
    scanf("%d %d", &a, &b);
    printf("%d", normalPower(a, b));
}

快速幂算法

如果数字更大，求2的1000000000的最后三位，上述代码一定是不能胜任的，于是需要使用快速幂算法

快速幂思路：每一步都把指数分成两半，而相应的底数做平方运算。

示例：

3^10=3*3*3*3*3*3*3*3*3*3

3^10=(3*3)*(3*3)*(3*3)*(3*3)*(3*3)
3^10=(3*3)^5
3^10=9^5
这样就从10次循环缩短到5次循环

所以如果幂数是偶数的话就直接/2，如果是奇数的话就先减一，将剩下的再/2
9^5=（9^4）*（9^1）
//此时我们抽出了一个底数的一次方，这里即为9^1，这个9^1我们先单独移出来,剩下的9^4又能够在执行“缩指数”操作了，把指数缩小一半，底数执行平方操作
9^5=（81^2）*(9^1)
//把指数缩小一半，底数执行平方操作
9^5=（6561^1）*(9^1)
//此时，我们发现指数又变成了一个奇数1，按照上面对指数为奇数的操作方法，应该抽出了一个底数的一次方，这里即为6561^1，这个6561^1我们先单独移出来，但是此时指数却变成了0，也就意味着我们无法再进行“缩指数”操作了。
9^5=（6561^0）*(9^1)*(6561^1)=1*(9^1)*(6561^1)=(9^1)*(6561^1)=9*6561=59049

代码

#include<iostream>
using namespace std;
int fastPower(int base, int power)
{
    long long result = 1;
    while (power > 0)
    {
        if (power % 2 == 0)
        {
            power /= 2;//把指数缩小为一半
            base = base*base % 1000;//底数变大成原来的平方，时刻进行取模防止溢出
        }
        else
        {
            power -= 1;//把指数减去1，使其变成一个偶数
            result = result*base % 1000;//此时记得要把指数为奇数时分离出来的底数的一次方收集好
            power /= 2;
            base = base*base % 1000;
        }
    }
    return result;
}
int main()
{
    int a, b;
    scanf("%d %d", &a, &b);
    printf("%d", fastPower(a, b));
}

因为power是一个整数，例如当power是奇数5时,power-1=4,power/2=2；而如果我们直接用power/2=5/2=2。在整型运算中得到的结果是一样的，因此，我们的代码可以压缩成下面这样：

int fastPower(int base, int power)
{
    long long result = 1;
    while (power > 0)
    {
        if (power % 2 != 0)
            result = result*base % 1000;//此时记得要把指数为奇数时分离出来的底数的一次方收集好
            power /= 2;
            base = base*base % 1000;
    }
    return result;
}

位运算优化

在C语言中，power%2==1可以用更快的“位运算”来代替，例如：power&1。因为如果power为偶数，则其二进制表示的最后一位一定是0；如果power是奇数，则其二进制表示的最后一位一定是1。将他们分别与1的二进制做“与”运算，得到的就是power二进制最后一位的数字了，是0则为偶数，是1则为奇数。例如5是奇数，则5&1=1；而6是偶数，则6&1=0；因此奇偶数的判断就可以用“位运算”来替换了。

同样，对于power=power/2来说，也可以用更快的“位运算”进行替代，我们只要把power的二进制表示向右移动1位就能变成原来的一半了。

int fastPower(int base, int power)
{
    long long result = 1;
    while (power > 0)
    {
        if (power &1)
            result = result*base % 1000;//此时记得要把指数为奇数时分离出来的底数的一次方收集好
            power >>=1;
            base = base*base % 1000;
    }
    return result;
}

参考：https://blog.csdn.net/qq_19782019/article/details/85621386