大数运算
大整数的存储
struct bigNum{
int d[1000]; //存储大整数
int len; //大整数的长度
bigNum()
{
memset(d, 0, sizeof(d));
len = 0;
}
};
在我们输入大数时,一般先用字符串读入,然后再把字符串另存至bigNum结构体。由于使用string数组读入时,整数的高位会变成数组的低位,而整数的低位会变成数组的高位,因此需要对其进行处理:
就是将string中的字符串反过来存放在结构体的数组中
bigNum change(string str)
{
bigNum a;
a.len = str.length(); //bigNum的长度就是字符串的长度
for(int i = 0;i<a.len;i++)
{
a.d[i] = str[a.len-i-1]-'0'; //逆序赋值
}
return a;
}
大整数的比较
如果要比较两个大数也非常简单:先判断两个大数的len,如果不相等,则以长的为大;如果相等,则从高位到低位进行比较,直到出现某位不等,就可以判断两个数的大小
int compare(bigNum a,bigNum b) //比较a,b的大小,返回1,0,-1
{
if(a.len>b.len) return 1;
else if(a.len<b.len) return -1;
else
{
for(int i = a.len-1;i>=0;i--) //从高往低比较
{
if(a.d[i]>b.d[i]) return 1;
else if(a.d[i]<b.d[i]) return -1;
}
return 0; //两位数相等
}
}
大整数的加法
对其中一位进行加法的步骤:将该位上的两个数字与进位相加,得到的结果取个位数作为改为的结果,取十位数作为新的进位。
注意事项:
1.两个数的最高位可能产生进位,判断最后的进位如果不是0的话要将进位加上!
2.注意有负数的运算:一个负数:去掉负号进行大整数减法;两个负数:去掉负号进行大整数加法
bigNum add(bigNum a,bigNum b)
{
bigNum c;
int carry = 0; //carry是进位
for(int i = 0;i<a.len||i<b.len;i++)
{
int temp = a.d[i]+b.d[i]+carry;
c.d[c.len++] = temp%10; //个位数为该位的结果
carry = temp/10; //十位数为新的进位
}
if(carry != 0) //如果最后进位不为0,则直接赋给最高位
{
c.d[c.len++] = carry;
}
return c;
}
大整数的减法
对某一步,比较被减位和减位,如果不够减,则令被减位的高位减1、被减位加10再进行减法;如果够减,则直接减。最后一步要注意减法后高位可能有多余0(743-742:347-247=100反001),要去除它们,但也要保证结果至少有一位数。
注意事项:在进行减法之前要先判断两个数的大小
bigNum sub(bigNum a,bigNum b)
{
bigNum c;
for(int i = 0;i<a.len||i<b.len;i++)
{
if(a.d[i]<b.d[i]) //如果不够减
{
a.d[i+1]--; //向高位借位
a.d[i]+=10; //当前位+10
}
c.d[c.len++] = a.d[i]-b.d[i];
}
while(c.len - 1>= 1&&c.d[c.len -1 ] == 0) //去除高位0
c.len--;
return c;
}
高精度与低精度乘法
取bigNum的某位与int型整体相乘再与进位相加,所得结果的个位作为该位的结果,高位部分作为新的进位。
注意事项:1.最后的最高位进位有可能不止一位,所以用while判断而不是用if
bigNum multi(bigNum a,int b)
{
bigNum c;
int carry = 0; //进位
for(int i = 0;i<a.len;i++)
{
int temp = a.d[i] * b + carry;
c.d[c.len++] = temp%10; //个位作为该位的结果
carry = temp/10; //高位部分作为新的进位
}
while(carry != 0)
{
c.d[c.len++] = carry%10;
carry/=10;
}
return c;
}
高精度与低精度除法
上一步的余数乘上10加上该步的位,得到该步临时的被除数,将其与除数比较;如果不够除,则该位的商为0;如果够除,则该位的商即为对应的商,余数即为对应的余数。最后一步要注意除法后高位可能会有多余的0,要去除它们,但也要保证结果至少有一位数。
bigNum divide(bigNum a,int b,int& r) //r为余数,初始时r = 0
{
bigNum c;
c.len = a.len; //被除数的每一位和商的每一位是一一对应的,因此先令其长度相等
for(int i = a.len-1;i>=0;i--)
{
r = r*10+a.d[i];
if(r<b) //如果不够除
c.d[i] = 0;
else //够除
{
c.d[i] = r/b; //商
r = r%b;
}
}
while(c.len - 1>=1&&c.d[c.len-1]==0)
{
c.len--;
}
return c;
}
例题:
https://blog.csdn.net/qq_42325947/article/details/104282613
#include<iostream>
#include<string>
using namespace std;
int main() {
string s;
int d,div,mod;
cin >> s>>d;
int len = s.length();
div = (s[0] - '0') / d;
mod = (s[0] - '0') % d;
if ( div != 0 || len == 1)
cout << div;
for (int i = 1; i < len; i++) {
div = (mod * 10 + (s[i] - '0')) / d;
cout << div;
mod = (mod * 10 + (s[i] - '0')) % d;
}
cout << ' ' << mod << endl;
return 0;
}
高精度与高精度乘法
即一个数的第 i 位和另一个数的第j 位相乘所得的数,一定是要累加到结果的第i+j 位上。然后再统一处理进位(为什么不同时处理乘法与进位?因为i=2,j=4与i=4,j=2都是在结果的第8位相加,所以一次无法处理完进位),当前的值加上进位的值再看本位数字是否又有进位。
bigNum multi(bigNum a, bigNum b)
{
bigNum c;
for (int i = 0; i < a.len; i++)
{
for (int j = 0; j < b.len; j++)
{
c.d[i + j] += (a.d[i] * b.d[j]); //先乘起来,后面统一进行进位, 注意是+=而不是=!
}
}
int i = 0;
for(i=0;i<MAX*2;i++)//进行进位
{
if(c.d[i]>=10) //若>=10
{
c.d[i+1]=c.d[i+1]+c.d[i]/10; //将十位上数字进位
c.d[i] = c.d[i] % 10; //将个位上的数字留下
}
}
while(c.len - 1>=1&&c.d[c.len-1]==0)
{
c.len--;
}
return c;
}
高精度与高精度除法
算法基本原理:就是被除数能减去除数多少次,减的次数就是商,减完剩下的部分就是余数。(用之前的函数模拟)
int compare(bigNum a,bigNum b) //比较a,b的大小,返回1,0,-1
{
if(a.len>b.len) return 1;
else if(a.len<b.len) return -1;
else
{
for(int i = a.len-1;i>=0;i--) //从高往低比较
{
if(a.d[i]>b.d[i]) return 1;
else if(a.d[i]<b.d[i]) return -1;
}
return 0; //两位数相等
}
}
bigNum sub(bigNum a,bigNum b)
{
bigNum c;
for(int i = 0;i<a.len||i<b.len;i++)
{
if(a.d[i]<b.d[i]) //如果不够减
{
a.d[i+1]--; //向高位借位
a.d[i]+=10; //当前位+10
}
c.d[c.len++] = a.d[i]-b.d[i];
}
while(c.len - 1>= 1&&c.d[c.len -1 ] == 0) //去除高位0
c.len--;
return c;
}
bigNum divide(bigNum a, bigNum b) //a是被除数,b是除数
{
int sum = 0;
while (compare(a, b) >= 0) //当a>=b就一直继续
{
a = sub(a, b);
sum++;
}
return a;
}
加速算法
当a= =b时,a/b= =1,余数是0。(a!=0,b!=0)
当a>b时,a/b>=1,余数需要通过计算求得。
当a<b时,a/b=0,余数就是a。
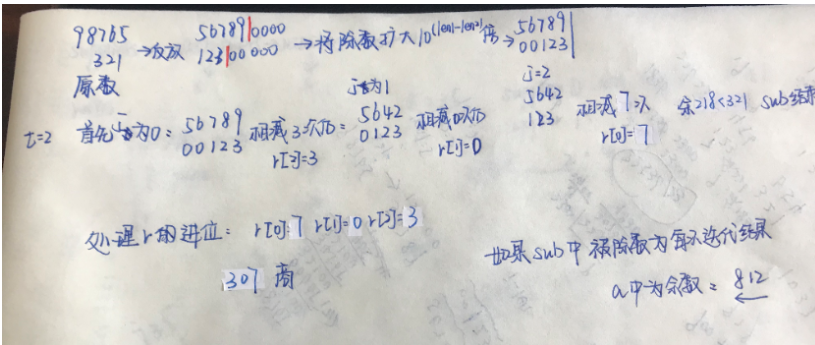
以28536 除以23 为例来看一下:开始商为0。
先减去23 的1000 倍,就是23000,发现够减1 次,余下5536,于是商的值就增加1000;
然后用5536减去2300,发现够减2 次,余下936,于是商的值增加200,即1200;
再用936 减去230,够减4 次,余下16,于是商值增加40,即1240。
最后,发现余下的数比23小,即为余数,即28536 / 23 得1240余16。
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int L=110;
int sub(int *a,int *b,int La,int Lb)
{
if(La<Lb) return -1;//如果a小于b,则返回-1
if(La==Lb)
{
for(int i=La-1;i>=0;i--)
if(a[i]>b[i]) break;
else if(a[i]<b[i]) return -1;//如果a小于b,则返回-1
}
for(int i=0;i<La;i++)//高精度减法
{
a[i]-=b[i];
if(a[i]<0) a[i]+=10,a[i+1]--;
}
for(int i=La-1;i>=0;i--)
if(a[i]) return i+1;//返回差的位数
return 0;//返回差的位数
}
//sub函数a-b进行操作,将结果留在a中
string div(string n1,string n2,int nn)//n1,n2是字符串表示的被除数,除数,nn是选择返回商还是余数
{
string s,v;//s存商,v存余数
int a[L],b[L],r[L],La=n1.size(),Lb=n2.size(),i,tp=La;//a,b是整形数组表示被除数,除数,tp保存被除数的长度
fill(a,a+L,0);fill(b,b+L,0);fill(r,r+L,0);//数组元素都置为0
for(i=La-1;i>=0;i--) a[La-1-i]=n1[i]-'0';
for(i=Lb-1;i>=0;i--) b[Lb-1-i]=n2[i]-'0';
if(La<Lb || (La==Lb && n1<n2))
{
//cout<<0<<endl;
return n1;
}//如果a<b,则商为0,余数为被除数
int t=La-Lb;//除被数和除数的位数之差
for(int i=La-1;i>=0;i--)//将除数扩大10^t倍 !!!!
if(i>=t) b[i]=b[i-t];
else b[i]=0;
Lb=La;
for(int j=0;j<=t;j++)
{
int temp;
while((temp=sub(a,b+j,La,Lb-j))>=0)//如果被除数比除数大继续减
//b+j:包括b前面的t-j个0,j++就是实现对b的10倍10倍的缩小,Lb-j是长度
{
La=temp;//temp返回的是相减后被减数的长度
r[t-j]++;//商的结果移到下一位
}
}
for(i=0;i<L-10;i++) r[i+1]+=r[i]/10,r[i]%=10;//统一处理进位
while(!r[i]) i--;//将整形数组表示的商转化成字符串表示的 ,同时处理前导0
while(i>=0) s+=r[i--]+'0';
//cout<<s<<endl;
i=tp;
while(!a[i]) i--;//将整形数组表示的余数转化成字符串表示的</span>
while(i>=0) v+=a[i--]+'0';
if(v.empty()) v="0";
//cout<<v<<endl;
if(nn==1) return s;
if(nn==2) return v;
}
int main()
{
string a,b;
while(cin>>a>>b){
cout<<div(a,b,1)<<endl;
cout<<div(a,b,2)<<endl;
}
return 0;
}
大数阶乘
求位数
方法一
原理:
lg(N!)=[lg(N*(N-1)*(N-2)*......*3*2*1)]+1
=[lgN+lg(N-1)+lg(N-2)+......+lg3+lg2+lg1]+1
求一个数的位数:
scanf("%d", &n);
printf("%d\n", (int)log10(n)+1);
#include<stdio.h>
#include<math.h>
int main()
{
int n;
double sum=0;
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
sum=sum+log10(i);
}
printf("%d\n",(int)sum+1);
return 0;
}
方法二
Stirling公式

#include<stdio.h>
#include<math.h>
#define PI 3.141592654
#define E 2.71828182846
int main()
{
int n,sum=1;
scanf("%d",&n);
if(n>3)
sum=log10(2*PI*n)/2+n*log10(n/E)+1;
printf("%d\n",sum);
return 0;
}
求阶乘
对于大数阶乘来说,最重要的是如何将每个数的每位数与相对应的数组元素储存起来,就如算50的阶乘,我们要先从1开始乘:
1*2=2,将2存到a[0]中,
接下来是用a[0]*3;
2*3=6,将6储存在a[0]中,
接下来是用a[0]*4;
6*4=24,是两位数,那么24%10= =4存到a[0]中,24/10==2存到a[1]中,
接下来是用a[0]5;a[1]5+num(如果前一位相乘结果位数是两位数,那么num就等于十位上的那个数字;如果是一位数,num==0)
24*5=120,是三位数,那么120%10= =0存到a[0]中,120/10%10= =2存到a[1]中,120/100==1存到a[2]中,
接下来是用a[0]3;a[1]6+num;a[2]*6+num;
120*6=720,那么720%10= =0存到a[0]中,720/10%10= =2存到a[1]中,720/100==7存到a[2]中,
...................
直到乘到50,将每一位数储存为止。
#include <stdio.h>
int main()
{
int a[20001];//储存每一位所得到的数
int temp,digit,n,i,j=0;//temp每次的得数 digit每次得数的位数
scanf("%d",&n);
a[0]=1;//从1开始乘
digit=1;//位数从第一位开始
for(i=2;i<=n;i++)
{
int num=0;
for(j=0;j<digit;j++)
{
temp=a[j]*i+num;//将一个数的每一位数都分别乘以i,
a[j]=temp%10;//将一个数的每一位数利用数组进行储存
num=temp/10;
}
while(num)//判断退出循环后,num的值是否为0
{
a[digit]=num%10;//继续储存
num=num/10;
digit++;
}
}
for(i=digit-1;i>=0;i--)//倒序输出每一位
printf("%d",a[i]);
printf("\n");
return 0;
}
参考:
https://blog.csdn.net/lovecyr/article/details/104883284
https://blog.csdn.net/wangaiji/article/details/80636641?depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-8&utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-8
https://blog.csdn.net/qq_36894136/article/details/79074728?depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-6&utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-6
https://blog.csdn.net/qie_wei/article/details/79508596


 浙公网安备 33010602011771号
浙公网安备 33010602011771号