树状数组
参考https://www.cnblogs.com/xenny/p/9739600.html
树状数组与线段树的区别
1.两者在复杂度上同级, 但是树状数组的常数明显优于线段树, 其编程复杂度也远小于线段树.
2.树状数组的作用被线段树完全涵盖, 凡是可以使用树状数组解决的问题, 使用线段树一定可以解决, 但是线段树能够解决的问题树状数组未必能够解决.
树状数组的介绍
(注意数组的下标时从1开始)
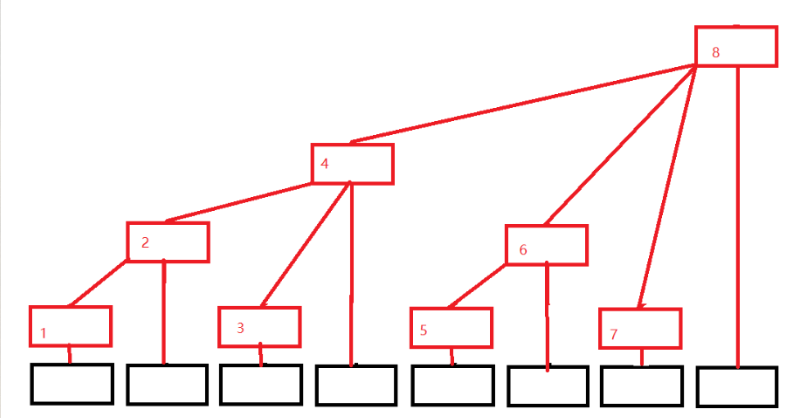
黑色数组代表原来的数组(下面用A[i]代替)
红色结构代表我们的树状数组(下面用C[i]代替)
- C[1] = A[1];
- C[2] = A[1] + A[2];
- C[3] = A[3];
- C[4] = A[1] + A[2] + A[3] + A[4];
- C[5] = A[5];
- C[6] = A[5] + A[6];
- C[7] = A[7];
- C[8] = A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8];
规律:
C[i] = A[i - 2k+1] + A[i - 2k+2] + ... + A[i];
k为i的二进制中从最低位到高位连续零的长度
树状数组的例题+代码
http://acm.hdu.edu.cn/showproblem.php?pid=1166
Input
第一行一个整数T,表示有T组数据。
每组数据第一行一个正整数N(N<=50000),表示敌人有N个工兵营地,接下来有N个正整数,第i个正整数ai代表第i个工兵营地里开始时有ai个人(1<=ai<=50)。
接下来每行有一条命令,命令有4种形式:
(1) Add i j,i和j为正整数,表示第i个营地增加j个人(j不超过30)
(2)Sub i j ,i和j为正整数,表示第i个营地减少j个人(j不超过30);
(3)Query i j ,i和j为正整数,i<=j,表示询问第i到第j个营地的总人数;
(4)End 表示结束,这条命令在每组数据最后出现;
每组数据最多有40000条命令
Output
对第i组数据,首先输出“Case i:”和回车,
对于每个Query询问,输出一个整数并回车,表示询问的段中的总人数,这个数保持在int以内。
Sample Input
1
10
1 2 3 4 5 6 7 8 9 10
Query 1 3
Add 3 6
Query 2 7
Sub 10 2
Add 6 3
Query 3 10
End
Sample Output
Case 1:
6
33
59
代码
#include <bits/stdc++.h>
using namespace std;
int n,m;
int a[50005],c[50005]; //对应原数组和树状数组
int lowbit(int x){
return x&(-x);
}
void updata(int i,int k){ //在i位置加上k
while(i <= n){
c[i] += k;
i += lowbit(i);
}
}
int getsum(int i){ //求A[1]~A[i]的和
int res = 0;
while(i > 0){
res += c[i];
i -= lowbit(i);
}
return res;
}
int main(){
int t;
cin>>t;
for(int tot = 1; tot <= t; tot++){
cout << "Case " << tot << ":" << endl;
memset(a, 0, sizeof a);
memset(c, 0, sizeof c);
cin>>n;
for(int i = 1; i <= n; i++){
cin>>a[i];
updata(i,a[i]); //输入初值的时候,也相当于更新了值
}
string s;
int x,y;
while(cin>>s && s[0] != 'E'){
cin>>x>>y;
if(s[0] == 'Q'){ //求和操作
int sum = getsum(y) - getsum(x-1); //x-y区间和也就等于1-y区间和减去1-(x-1)区间和
cout << sum << endl;
}
else if(s[0] == 'A'){
updata(x,y);
}
else if(s[0] == 'S'){
updata(x,-y); //减去操作,即为加上相反数
}
}
}
return 0;
}
代码解析:
int lowbit(int x){
return x&(-x);
}
其中的x&(-x):
当一个偶数与它的负值向与时,结果是能被这个偶数整除的最大的2的n次幂
当一个奇数与它的负值向与时结果一定是1.
用途1 单点更新 区间查询
单点更新
void updata(int i,int k){ //在i位置加上k
while(i <= n)//注意是小于等于n,不是小于n!!!!
{
c[i] += k;
i += lowbit(i);
}
}
//*************************************
for(int i = 1; i <= n; i++){
cin>>a[i];
updata(i,a[i]); //输入初值的时候,也相当于更新了值
}
例如i==1:c[1]=c[1]+a[1]; i=i+1=2;
c[2]=c[2]+a[2]; i=i+2=4;
c[4]=c[4]+a[4]; i=i+4=8;
c[8]=c[8]+a[8]; i=i+8=16结束 将a[]数组中所有需要加a[1]的全都加了
区间查询
int getsum(int i){
int res = 0;
while(i > 0){
res += c[i];
i -= lowbit(i);
}
return res;
}
例如:求a[1]到a[8]的和:也就是c[8]的值:
res=res+c[8]; i=i-8=0;结束
再例如:求a[1]到a[7]的和:
res=res+c[7] i=i-1=6 a[7]
res=res+c[6] i=i-2=4 a[6] a[5]
res=res+c[4] i=i-4=0 a[4] a[3] a[2] a[1]
用途2:区间更新 单点查询
这里我们引入差分,利用差分建树。
规定A[0]=0
A[] =0 1 2 3 5 6 9//原数组
D[] =0 1 1 1 2 1 3//差分数组(d[i]=a[i]-a[i-1])
如果我们把[2,5]区间内值加上2,则变成了
A[] =0 1 4 5 7 8 9
D[] =0 1 3 1 2 1 1
当某个区间[x,y]值改变了,区间内的差值是不变的,只有D[x]和D[y+1]的值发生改变
这样就把,原来要更新一个区间的值变成了只需要更新两个点。
代码:
int n,m;
int a[50005] = {0},c[50005]; //对应原数组和树状数组
int lowbit(int x)
{
return x&(-x);
}
void updata(int i,int k)
{ //在i位置加上k
while(i <= n)
{
c[i] += k;
i += lowbit(i);
}
}
int getsum(int i)
{ //求D[1 - i]的和,即A[i]值
int res = 0;
while(i > 0)
{
res += c[i];
i -= lowbit(i);
}
return res;
}
int main(){
cin>>n;
for(int i = 1; i <= n; i++)
{
cin>>a[i];
updata(i,a[i] - a[i-1]); //输入初值的时候,也相当于更新了值
}
//[x,y]区间内加上k
updata(x,k); //d[x]需要增加k,所以相应的c[]数组中需要增加的都要增加
updata(y+1,-k);
//查询i位置的值,就是查询a[i]的值,就是求从d[0]到d[i]的和,就是借c[]数组用getsum函数求和 (单点查询)
int sum = getsum(i);
return 0;
}
区间更新:
updata(i,a[i] - a[i-1]);
updata(x,k);
updata(y+1,-k);
单点查询:
int sum = getsum(i);
用途3:区间查询 区间更新
思路:https://blog.csdn.net/bestsort/article/details/80796531
怎么求呢?我们基于问题2的“差分”思路,考虑一下如何在问题2构建的树状数组中求前缀和:
位置p的前缀和 =
在等式最右侧的式子中,
被用了p次,
被用了
次……那么我们可以写出:
位置p的前缀和 =
那么我们可以维护两个数组的前缀和:
一个数组是
另一个数组是
int n,m;
int a[50005] = {0};
int sum1[50005]; //(D[1] + D[2] + ... + D[n])
int sum2[50005]; //(1*D[1] + 2*D[2] + ... + n*D[n])
int lowbit(int x){
return x&(-x);
}
void updata(int i,int k){
int x = i; //因为x不变,所以得先保存i值
while(i <= n){
sum1[i] += k;
sum2[i] += k * (x-1);
i += lowbit(i);
}
}
int getsum(int i){ //求前缀和
int res = 0, x = i;
while(i > 0){
res += x * sum1[i] - sum2[i];
i -= lowbit(i);
}
return res;
}
int main(){
cin>>n;
for(int i = 1; i <= n; i++){
cin>>a[i];
updata(i,a[i] - a[i-1]); //输入初值的时候,也相当于更新了值
}
//[x,y]区间内加上k
updata(x,k); //A[x] - A[x-1]增加k
updata(y+1,-k); //A[y+1] - A[y]减少k
//求[x,y]区间和
int sum = getsum(y) - getsum(x-1);
return 0;
}
区间更新
void updata(int i,int k){
int x = i; //因为x不变,所以得先保存i值
while(i <= n){
sum1[i] += k;
sum2[i] += k * (x-1);
i += lowbit(i);
}
}
updata(x,k); //A[x] - A[x-1]增加k
updata(y+1,-k); //A[y+1] - A[y]减少k
区间查询
//求[x,y]区间和
int sum = getsum(y) - getsum(x-1);
用途4:求逆序对
1.逆序对的定义
逆序对就是序列a中ai>aj且i<j的有序对。
方法一:未进行离散化
我们可以先开一个大小为a的最大值的数组 t,每当读入一个数时,我们可以用桶排序的思想,将t[a[i]]加上1,然后我们统计t[1]~t[a[i]]的和ans,ans - 1(除掉这个数本身)就是在这个数前面有多少个数比它小。我们只要用i-ans就可以得出前面有多少数比它大,也就是逆序对的数量。
#include <iostream>
#include<string>
#include<algorithm>
#define lowbit(x) (x)&(-x)
using namespace std;
const int maxn = 1e6 + 10;
int c[maxn], n, result;
void update(int i)
{
while (i <= maxn)
{
c[i]++;
i += lowbit(i);
}
}
int getsum(int i)
{
int ans = 0;
while (i > 0)
{
ans += c[i];
i -= lowbit(i);
}
return ans;
}
int main()
{
int temp;
scanf("%d", &n);
for (int i = 1; i <= n; i++)
{
scanf("%d", &temp);
update(temp);
result += i - getsum(temp);//使用i减去前面比自己小的就是比自己大的
}
printf("%d\n", result);
return 0;
}
方法二:离散化
现在这个代码可以在数的最大值比较小的时候可以正确的得出答案,如果数据很大,这回造成我们要开的空间很大。
我们是否可以适当的减少空间的需求呢?我们看看下面这些数:
1 2 3 4 5 10
这6个数我们需要使用大小10的数组来存储,我们仔细想想,可以发现中间 6 7 8 9 这4个位置是没有用到的,也就是说这4个空间被浪费了。怎样减少这样的浪费呢?
我们可以在读完数数据后对他进行从小到大排序,我们用排完序的数组的下标来进行运算。这样可以保证小的数依旧小,大的数依旧大。这一步叫做离散化。
#include<iostream>
#include<string>
#include<cstring>
#include<algorithm>
using namespace std;
struct node
{
int data;
int index;
}list[1000];
int aa[1000], c[1000];
int n;
int lowbit(int x)
{
return x&(-x);
}
bool cmp(struct node &a, struct node&b)
{
return a.data < b.data;
}
void update(int i)
{
while (i <=n)
{
c[i] +=1;
i += lowbit(i);
}
}
int getsum(int i)
{
int ans = 0;
while (i > 0)
{
ans += c[i];
i -= lowbit(i);
}
return ans;
}
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; i++)
{
scanf("%d", &list[i].data);
list[i].index = i;
}
sort(list+1, list + n+1, cmp);
for (int i = 1; i <= n; i++)
aa[list[i].index] = i;
long long answer = 0;
for (int i = 1; i <= n; i++)
{
update(aa[i]);
answer += i - getsum(aa[i]);//用来存储原数第i个数的order下标是什么
}
cout << answer;
}
或者不用aa数组
/*for (int i = 1; i <= n; i++)
aa[list[i].index] = i;*/
long long answer = 0;
for (int i = 1; i <= n; i++)
{
update(list[i].index);
answer += i - getsum(list[i].index);//用来存储原数第i个数的order下标是什么
}
用途5:求区间最大值
void update(int i ,int k)
{
while (i <= n)
{
c[i] = max(c[i], k);
i += lowbit(i);
}
}
int getsum(int i)
{
int ans = 0;
while (i > 0)
{
ans=max(ans, c[i]);
i -= lowbit(i);
}
return ans;
}
改进:
二维树状数组
C[x][y]记录的是右下角为(x, y),高为lowbit(x), 宽为 lowbit(y)的区间的区间和。
单点修改 区间查询
单点修改
void updata(int x,int y,int k)//将点(x, y)加上z
{ int memy=y;
while(x <= n)
{
y=memy;
while(y<=n)
{
c[x][y]+=k;
y+=lowbit(y);
}
x+=lowbit(x);
}
}
区间查询
int getsum(int x int y)
{ //求前缀和
int res = 0, memy=y;
while(x>0)
{
y=memy;
while(y>0)
{
res += c[x][y];
y -= lowbit(y);
}
x-=lowbit(x);
}
return res;
}
区间修改 单点查询
二维前缀和:
那么我们可以令差分数组表示
与
的差。
下面是给最中间的3*3矩阵加上x时,差分数组的变化:
0 0 0 0 0
0 +x 0 0 -x
0 0 0 0 0
0 0 0 0 0
0 -x 0 0 +x
效果:
0 0 0 0 0
0 x x x 0
0 x x x 0
0 x x x 0
0 0 0 0 0
void add(int x, int y, int z){
int memo_y = y;
while(x <= n){
y = memo_y;
while(y <= n)
tree[x][y] += z, y += y & -y;
x += x & -x;
}
}
//与单点修改 区间查询的add一样
void range_add(int xa, int ya, int xb, int yb, int z){
add(xa, ya, z);
add(xa, yb + 1, -z);
add(xb + 1, ya, -z);
add(xb + 1, yb + 1, z);
}//分别对四个特殊位置进行加减运算
void ask(int x, int y){
int res = 0, memo_y = y;
while(x){
y = memo_y;
while(y)
res += tree[x][y], y -= y & -y;
x -= x & -x;
}
}

