zk

整理了一些零知识证明的学习资料，需要的话自取


zk-SNARK：
从零开始学习zk-SNARK系列：
1、从零开始学习zk-SNARK(一)-多项式的性质与证明
2、从零开始学习zk-SNARK(二)-多项式的非交互式零知识证明
3、从零开始学习zk-SNARK(三)—从程序到多项式的构造
4、从零开始学习zk-SNARK(四)—多项式的约束
5、从零开始学习zk-SNARK(五)—Pinocchio 协议
零知识证明 - zkSNARK入门
简述零知识证明与zkSNARK
零知识证明-zkSNARK应用场景分析
零知识证明 - zkSNARK应用的Nullifier Hash攻击
零知识证明-ethsnarks源代码导读

浅谈零知识证明系列：
1、浅谈零知识证明：背景与起源
2、浅谈零知识证明之二：简短无交互证明（SNARK）

探索零知识证明系列：
1、探索零知识证明系列1 - 初识「零知识」与「证明」
2、探索零知识证明系列2 - 从「模拟」理解零知识证明
3、探索零知识证明系列3 - 寻找「知识」
4、探索零知识证明系列4 - 亚瑟王的「随机」挑战
5、探索零知识证明系列5-构建非交互式零知识证明

Zcash：
Zcash - 各种密钥和签名，你懂吗？
Zcash - 图解Transaction结构

libsnark：
零知识证明 Learn by Coding：libsnark 入门篇
零知识证明 - libsnark源代码分析

Groth16算法：
零知识证明 - Groth16算法介绍
零知识证明 - Groth16计算详解

DIZK：
零知识证明 - DIZK介绍
零知识证明 - DIZK源代码导读

EYBlockchain:
利用 EYBlockchain 在以太坊上创建隐私币
零知识证明 - 再谈EYBlockchain

应用：
路印3.0：使用零知识证明提升去中心化的交易性能
零知识证明-Mixer(混币)应用分析

其他：
零知识证明-Semaphore源代码导读
零知识证明 - 从QSP到QAP
零知识证明 - 深入理解ZoKrates
零知识证明 - 一种新型的Merkle树（Shrubs）
区块链-深入理解Uniswap协议
零知识证明-R1CS导入导出
零知识证明 - 椭圆曲线基础
理解零知识证明算法之 Zk-stark
利用 AZTEC 协议进行匿名隐私转账

 

 

 

 

 

本文分为两部分，第一部分说明零知识能干什么，为什么它这么强大，在区块链中这么火；第二部分比较零知识证明的算法zkSNARK, zkSTARKs, zkBoo, Sonic和BulletProofs的特性。

第一部分

使用零知识算法能干什么？

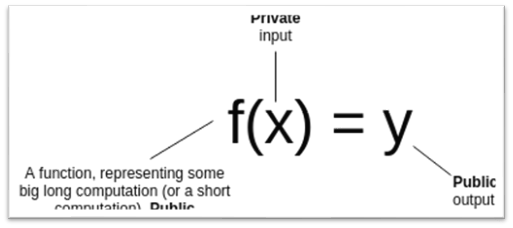
设定一个场景，现有一个公共的函数f和一个函数的输出值y，Alice对Bob说她知道x值，但是Bob不信。x可能是Alice花费了很多资源才得来的，为了向Bob证明她知道x同时又不泄露x给Bob，该怎么办？

Alice于是使用零知识证明算法，也就是前面提到的算法，来生成一个证明 [公式] 。Bob认证[公式]，确认Alice是不是真的知道满足函数f的x。

这个函数f是一个通用的函数，只要没有无限循环，那么就能够满足要求来生成证明[公式]。在生成[公式]之前，需要将函数f转换成特定的格式，现已经有专门的工具，如下图。C表示高级编程语言的一个函数。

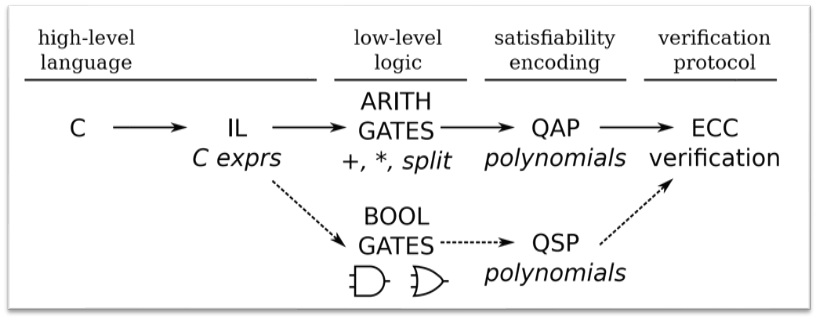B. Parno, “Pinocchio: Nearly Practical Verifiable Computation,” in 2013

这样的话，零知识证明就可以应用在很多方面，比如：

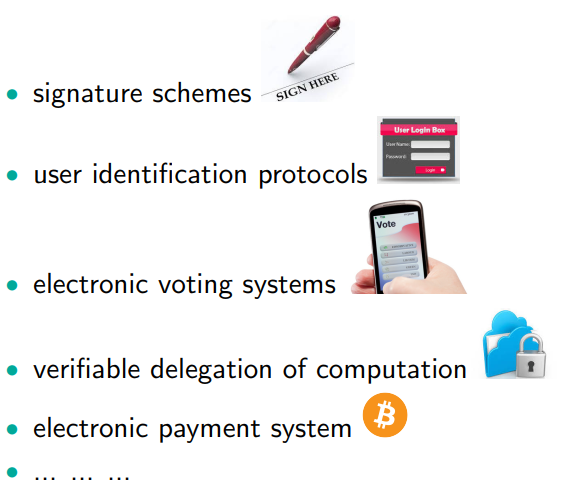
使用零知识证明，我能完成签名，但又不暴露我是谁；我能匿名投票；我能匿名转账（zerocash和zerocoin）。概况起来就是：我能证明我的所作所为是符合协议（要求）的，但我不告诉你我做了什么or我是谁（认证者没有从我这里学到有用的信息/知识）。

要生成零知识证明[公式]，现有比较优秀的算法，分别是：zkSNARK, zkSTARKs, zkBoo, Sonic和BulletProofs。

我们的目的是能否将这些算法应用在区块链中，实现下面的愿景，改善现有区块链系统的scalability：

•生成"π"的时间复杂度（越小越好）

•"π"的大小（越小越好）

•认证"π"的时间复杂度（越小越好）

•需不需要trusted setup？（最好不需要）

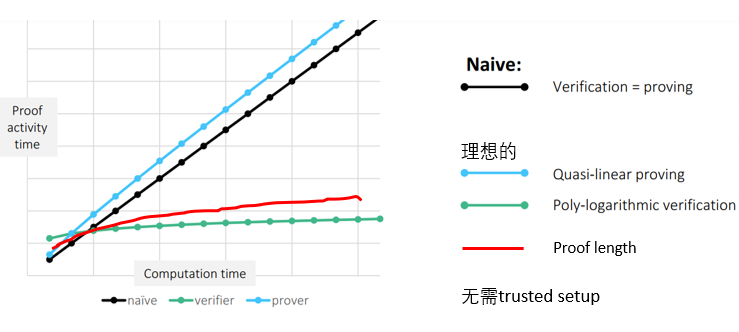
如果有一个零知识证明算法能够满足下图所示的条件：

  1. 生成证明π的计算复杂度最多是线性的。
  2. 认证π的计算复杂度最多是对数的。
  3. π的大小复杂度最多是对数的。（随着x和f的大小增大，呈对数增长）。
  4. 无需trusted setup。（后面会讲）

那么我们就认证这是一个“理想的”零知识证明算法。为什么？

因为使用这样的算法，我就能将现有的区块链系统设计成下图所示的样子。区块链可以不用保存原始的交易数据，而是保存证明π，用来证明交易的一致性。矿工不再是重复通过认证原始交易数据来认证，而是通过验证π。而π （1）小于原始交易数据；（2）认证时间比原来的验证方式短。这样可以提高区块链的拓展性。

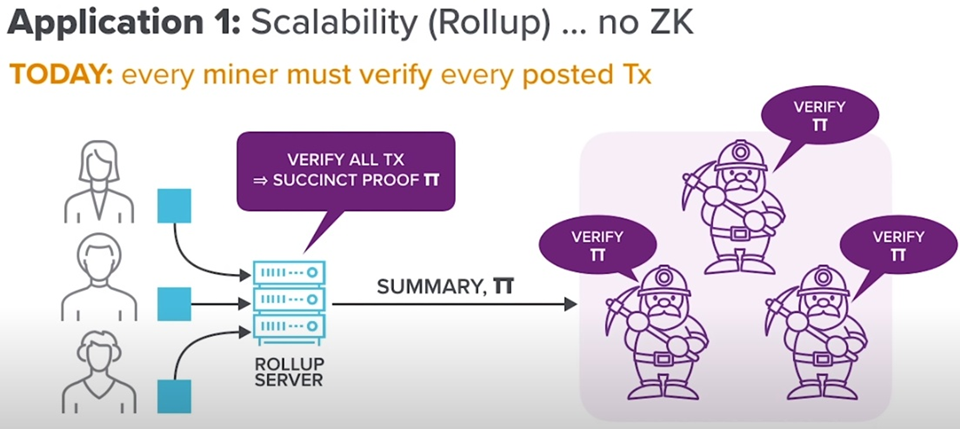
现有一个问题，现在有没有存在满足上面要求的零知识证明算法呢？结果是：还没有，但比较接近了。

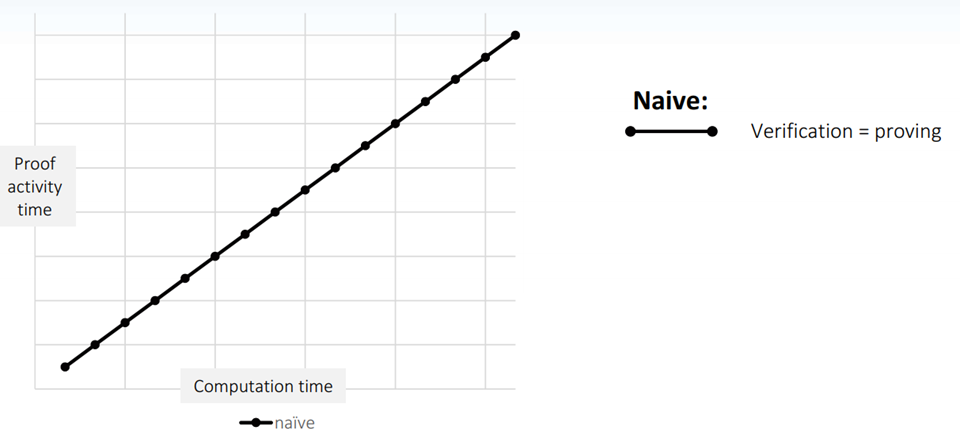
下面我们比较这几种零知识证明算法的特性。假如最原始的（证明-认证）的方式是重复计算的方式：在f(x)=y中，证明者和验证者通过直接执行x来验证结果。现在比特币系统就是使用这样的方式。那么这样子生成证明（其实没有生成）的计算复杂度和验证证明的计算复杂度是一样的。

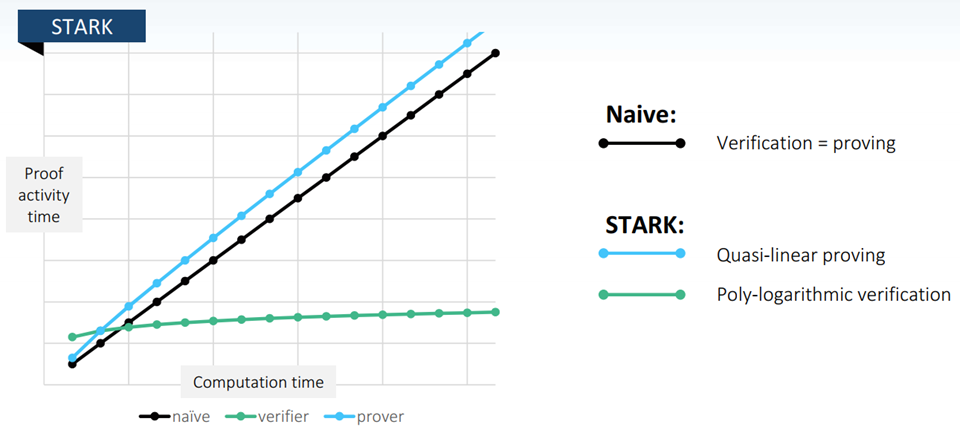
zk-STARK的性能表示成下图所示。它生成证明的时间复杂度随着输入和函数f的复杂度线性变化。而认证的时间复杂度是对数的。

将图中交叉点的部分放大，发现虽然生成证明的时间复杂度是线性的，但它比原始的方式慢100多倍。

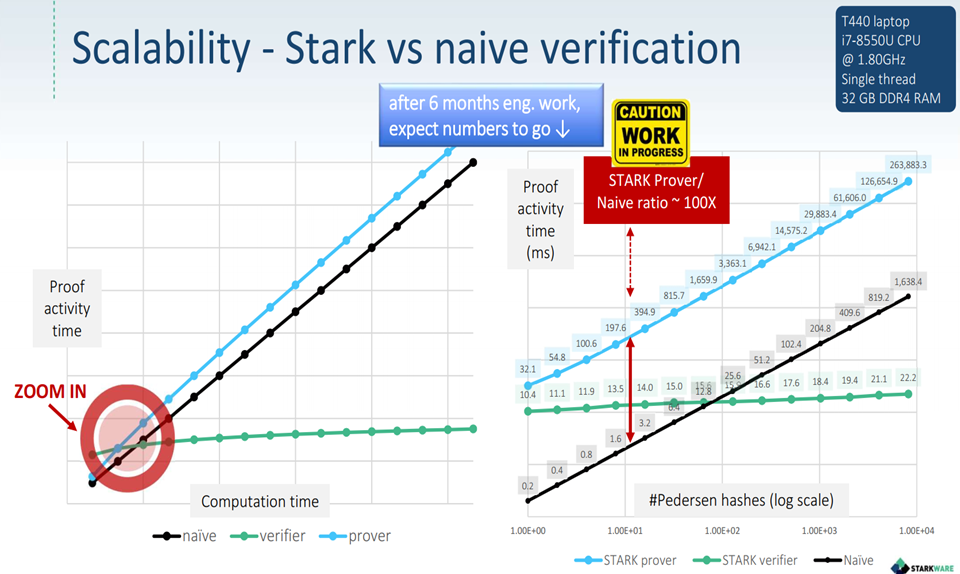
生成一个一百多层的merkle树的零知识证明大概需要几秒钟；而认证该证明只需要十几毫秒。

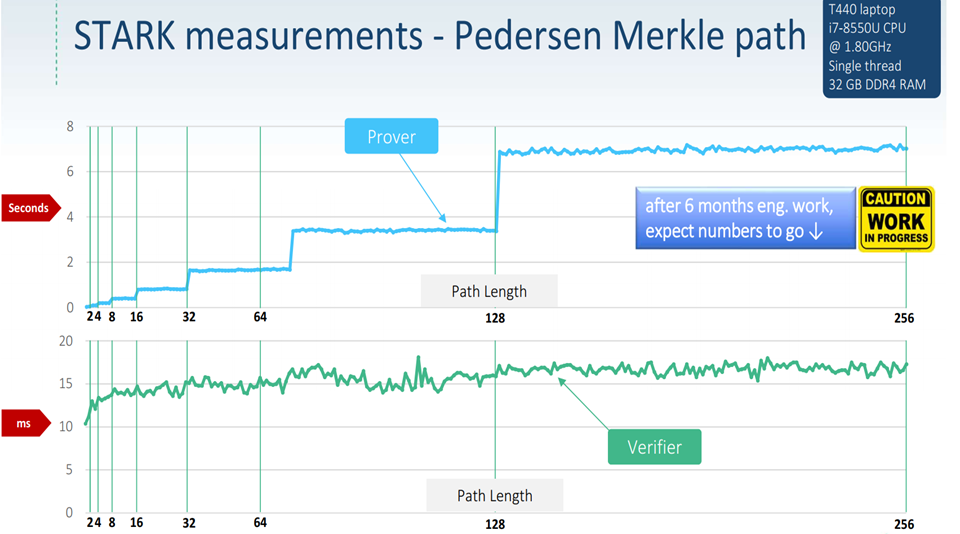
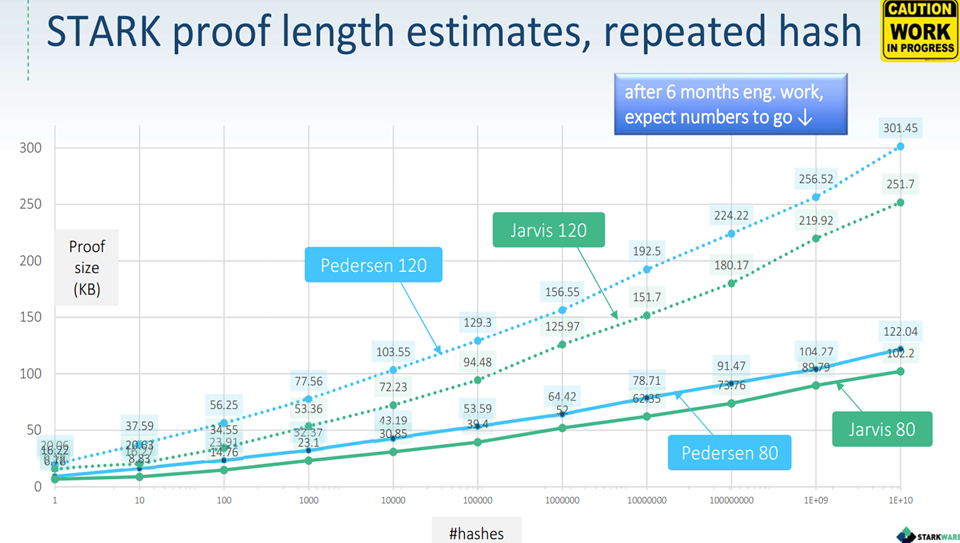
zk-STARK所生成的证明的大小的复杂度（基本）是线性的。计算1E+10次的hash函数所生成的证明大概是300KB。

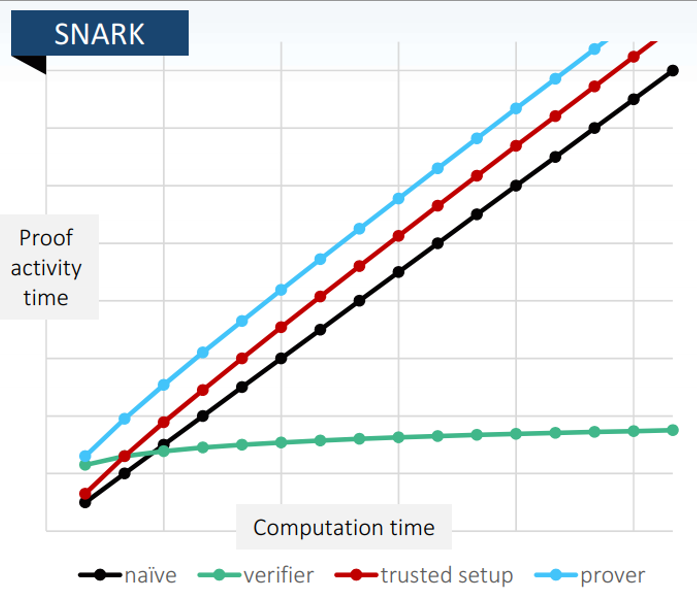
zk-SNARK是2013年就提出的零知识证明算法，被用在zerocoin上面来实现匿名货币的功能。它的特性如下图所示。它的缺点是需要trusted setup。

什么叫trusted setup？在协议进行证明和认证之前，需要设置和生成一些公共的参数。但是在生成这些公共参数的过程中，生成了一些不能公开的中间数据，需要在完成setup之后把这部分不能公开的数据删除。任何一方拿到这些数据都能够破解协议。问题是：如何保证这些数据真正被删除了呢？解决这个问题的方法之一是使用多方计算的方式来生成这些公共参数，只要一方是诚信的，该协议就是安全的；另一个方法是2019年提出来发表在CCS上的名为Sonic方法，它让这些参数能够不断更新，只要当前的更新者是诚信的，那么当前的参数（包含之前的）就是安全的。

Recursive Snark（Coda）改善了zk-SNARK的trusted setup的计算时间复杂度的问题，让在setup的时候生成这些公共参数的时间复杂度不再是线性增长的。如下图红色线段部分。

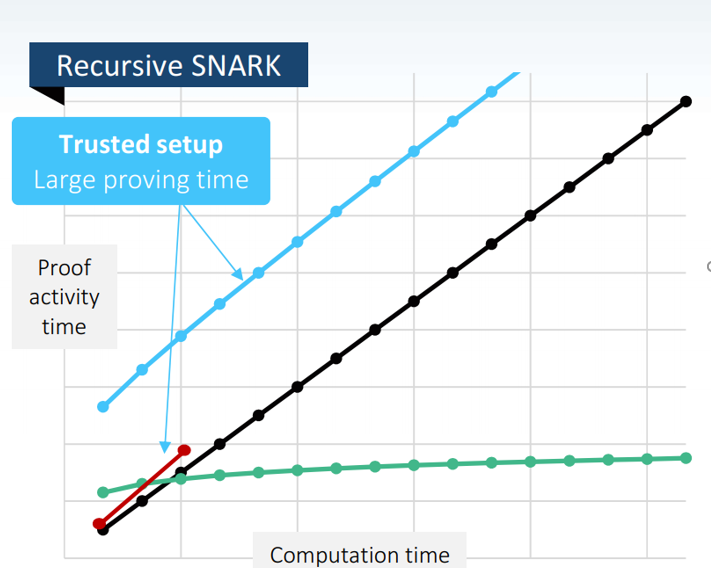
BulletProofs是18年提出来的方法，它的一个优点是它所生产的证明的大小是对数变换的。这很有利于将证明保存在区块链中，即使x和函数f很大。只是它的认证的计算复杂度是线性的。

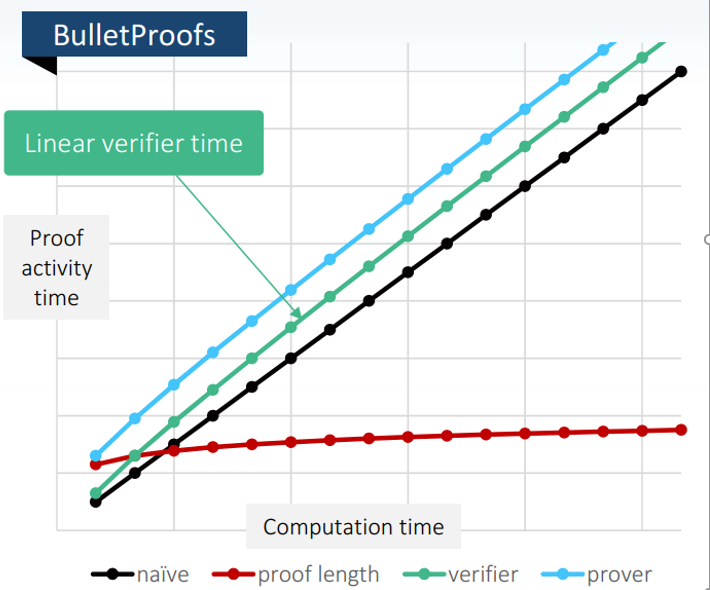
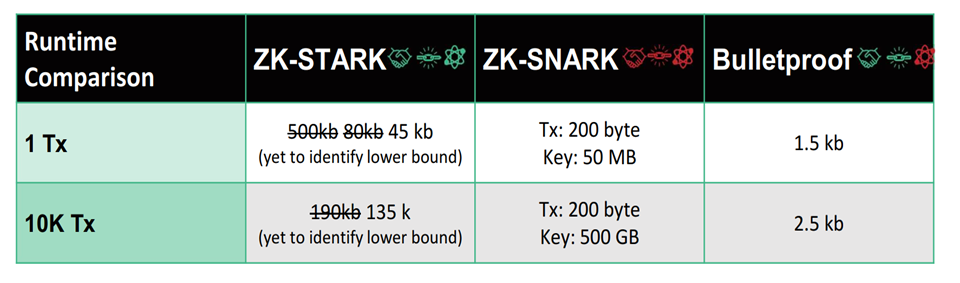
下图进一步比较了zk-STARK, zk-SNARK和Bulletproof的性能。STARK和Bulletproof无需trusted setup，而且后者的证明的大小随着交易数量的急剧增加只变大了一点点。

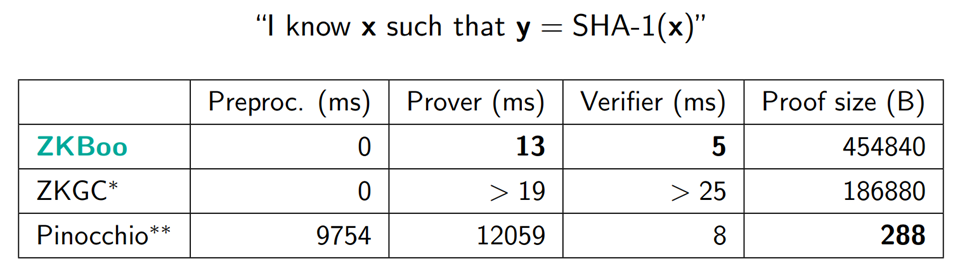
最后讲讲2016年提出来的zkBoo，它的特点是：生成证明和认证证明的时间复杂度是对数的（超快），但是所生成的证明的大小是线性增长的，具体看下表。个人觉得，这样的特性不是很适合应用在区块链中。因为将它的证明保存在区块链中将会带来很大的存储开销。

 

谢谢

 

zk-STARK作者的演讲：


M. Maller, S. Bowe, M. Kohlweiss, and S. Meiklejohn, “Sonic: Zero-Knowledge SNARKs from Linear-Size Universal and Updateable Structured Reference Strings,” 099, 2019. Accessed: Nov. 12, 2020. [Online]. Available: .

I. Miers, C. Garman, M. Green, and A. D. Rubin, “Zerocoin: Anonymous Distributed E-Cash from Bitcoin,” in 2013 IEEE Symposium on Security and Privacy, May 2013, pp. 397–411, doi: 10.1109/SP.2013.34.


E. B. Sasson et al., “Zerocash: Decentralized Anonymous Payments from Bitcoin,” in 2014 IEEE Symposium on Security and Privacy, May 2014, pp. 459–474, doi: 10.1109/SP.2014.36.


I. Giacomelli, J. Madsen, and C. Orlandi, “ZKBoo: Faster Zero-Knowledge for Boolean Circuits,” p. 16.

B. Bunz, J. Bootle, D. Boneh, A. Poelstra, P. Wuille, and G. Maxwell, “Bulletproofs: Short Proofs for Confidential Transactions and More,” in 2018 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, May 2018, pp. 315–334, doi: 10.1109/SP.2018.00020.

 

 

posted @ 2021-09-23 16:18  zJanly  阅读(587)  评论(0)  编辑  收藏  举报