fft
下面我们只考虑圆周卷积的情况， * 代表圆周卷积，
对于一维列向量，a 和 b， 假设c = a*b
由于卷积是一个有限维度的线性运算，那么可以表达为矩阵向量的乘法形式
这里面 M 是一个 Circulant Matrix，而Circulant Matrix 是一种特殊的 Toeplitz Matrix 可以被 DFT Matrix 对角化。
那么
从右往左看这里面 是b 的傅里叶变换，
是逐点相乘，FLOPS很便宜，
是逆傅里叶变换。 这里面由于傅里叶变换的属性，我们存在快速解法， MIT 著名线性代数教授Gilbert Strang 曾经描述过FFT 算法可能是我们一生当中最重要的数值方法，他从
降低到了
。这样子我们每一步都能有一个比较省flops 的操作，那么整体上我们能够有一种相对快的方法。
但是实际生活当中用zero padding FFT 作快卷积，不一定快，尤其是当卷积一方比较 小的时候，或者为了满足类似 这样的 zero padding使得padding 长度过大，那么fft 做卷积都是慢的。只有当两者长度可比拟时候fft的优势才能体现出来。
所以由此延伸出更好的overlap discard， overlap save等快速卷积方法，可以改善上述问题： https://en.wikipedia.org/wiki/Overlap%E2%80%93save_method
备注 1： FFT 其实是一种特殊的范德蒙矩阵， 范德蒙矩阵的一类子集都存在矩阵向量相乘的快速数值方法，比如Fast Walsh Hadmard Transform等 https://en.wikipedia.org/wiki/Fast_Walsh%E2%80%93Hadamard_transform
备注 2： 但是!但是！ 所有上述推导都是纯理论的flops比较，但是实际上flops小的速度并不一定快！！！！我的数值线性代数教授反复给我们强调过这一点！！！！
是否能够减少overhead， 还有能否充分调用CPU/GPU 性能， 是否高度可并行化很多时候才能在实际生活中真正决定速度，纸上得来终觉浅哈，理论固然重要，但是不要轻易相信任何数值方法给的结论，最重要的是真的在实际生活中在对应的硬件软件平台上跑一跑才知道的。
这是一个DFT：
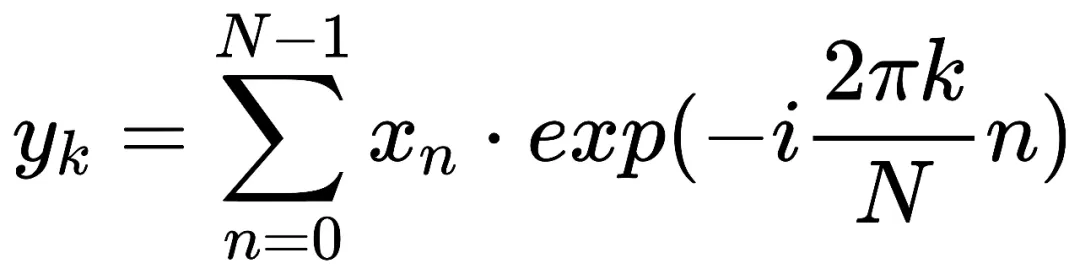
- k表示每N个样本的循环次数；
- N表示信号的长度；
- 表示信号在样本n处的值。
一个信号可以表示为所有正弦信号的和。
yk是一个复值，它给出了信号x中频率为k的正弦信号的信息；从yk我们可以计算正弦的振幅和相位。
换成矩阵式，它就变成了这样：
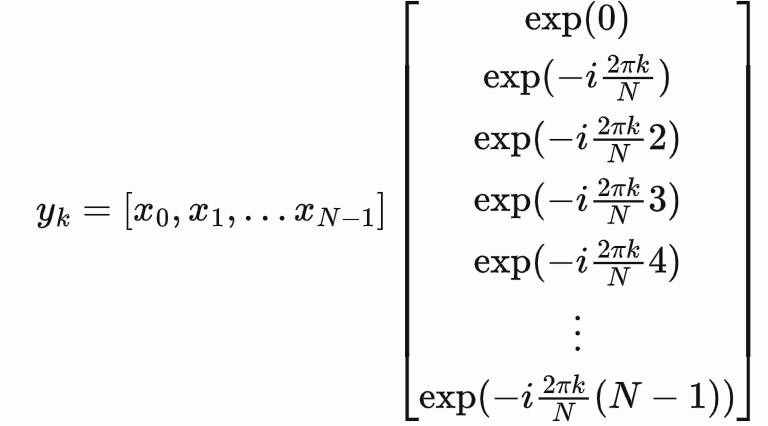
这里给出了特定值k的傅里叶值。
不过通常情况下，我们要计算全频谱，即k从[0,1,…N-1]的值，这可以用一个矩阵来表示（k按列递增，n按行递增）：
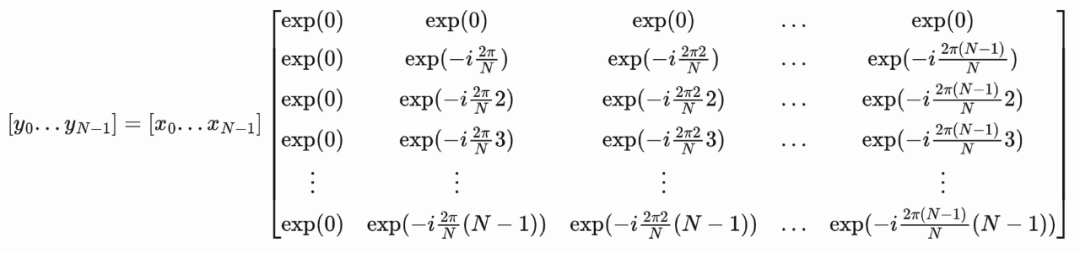
简化后得到
