Pairing friendly curve

 https://zhuanlan.zhihu.com/p/104531745

 

 

作者：咕噜咕噜
链接：https://zhuanlan.zhihu.com/p/350346362
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

Pairing在椭圆曲线密码中起着很大的作用，它是许多密码协议的基础。本文的目的是：介绍pairing的基本数学原理，以及实现时应注意的问题。为了方便，我们针对国密算法SM9所指定的曲线（BN曲线）来说明，有关SM9算法的具体描述，可参考SM9标准。首先，从宏观上来看双线性对，它就是这样的一个双线性映射：

，其中 是三个群， 是椭圆曲线上的两个子群，而 是有限域中的一个乘法子群。所谓“双线性”是指，对于 ，有

，这里将 视为乘法群，当然也可以将其视为加法群，即 。

配对类型：

• 
• ，但这两个群之间有着一个可以高效计算的同构映射
• ，不存在可以高效计算的同构映射

首先，我们先来介绍一个定理，它是搞清楚椭圆曲线群结构的基础：

定理：设 ， ，设 是一个素数，且 ，定义 ，易证 是 的阶为 的子群。假设 是满足 的最小的正整数（ 称为是关于 的嵌入次数），令 ，那么 是一个 的子群，而且它同构于两个 阶循环群的直积。

这个定理说明了，在基域上所有 阶点和 构成 阶循环群，然后将域扩张到满足定理中的 这个条件，那么这时在扩域上，所有 阶点和 构成了一个 阶的群。而且这个 阶群是两个循环群的直积，进一步，由于这个群中所有元素的阶（除单位元）都是 ，我们在这个群中随意找一个 阶元 ，由它可生成一个 阶子群，然后在这个子群之外再随意找一个 阶元 ，那么显然 也生成了一个 阶子群，而且 各自生成的子群的交就是单位元，因此，我们按照这个方法继续找 ，这样，我们把 阶群写成了 个 阶子群的并集，这些 阶群的交集是单位元。

A toy example：设 ， ，这时可以计算出 ，令 ，那么显然 是7阶循环群。由于 ，因此嵌入次数 ，我们利用 上的不可约多项式 ，将基域扩张为 ，根据上面的定理， ，而且它可以分成8个7阶循环群的并集，如下图：

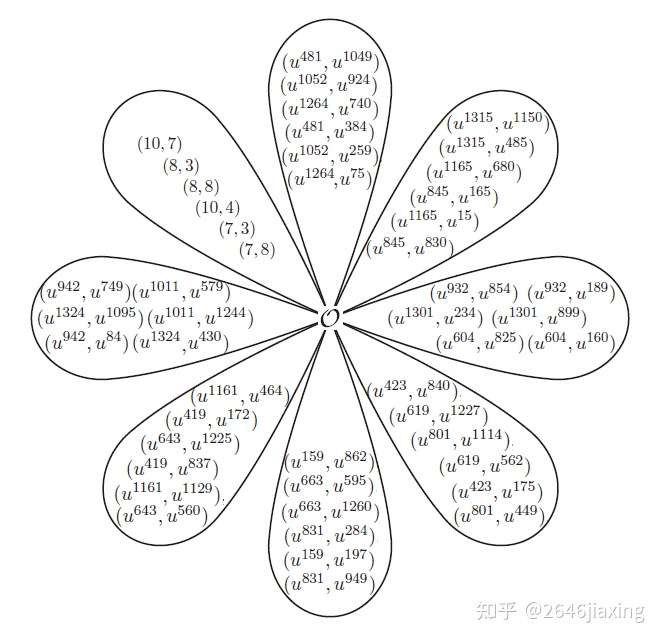
在上图中，我们观察，左上角的那个子群中的点的坐标都是在基域上的，而其他子群的点的坐标都是在扩域上的，实际上这个群就是我们在pairing中的 ，但是 是哪个群呢？到目前为止还无法说清楚，见后续哟。

 

 

 

 

 

续接上文，本节的主要目的是搞清楚pairing中 群 是哪个群，上文中说到，  就是在坐标在基域上的点构成的  阶循环子群。

首先，我们先对  中的元素定义以下三个映射：

1. Frobenius map  ： 
2. Trace  : 
3. anti-Trace  :  ，其中  表示点乘运算。

现在，我们来看  中的点在这些映射下是怎样变化的，首先由于  中的点的坐标都是基域  上的，因此，在Frobenius映射  下，其中的点都是不动的，即  在  上是恒同变换。对于  ，  ，由于  ，这说明  在  的作用下是不动的，因此，  。又因为  ，因此，  将  中所有的点都映射到  。到此，我们可以将  写为：

上面定义的Frobenius map在  上是恒同映射，但在  中的另一个  阶子群上，有  （暂不证明），我们记这个子群为  ，因此类比于  的写法，我们可以将  写为：

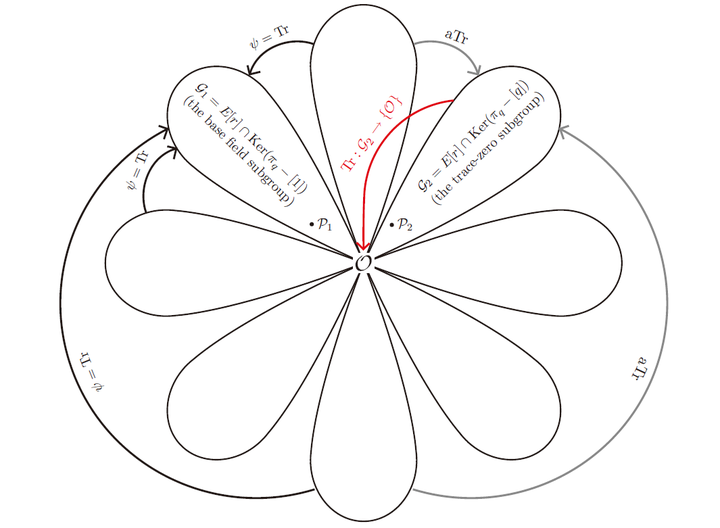
而且可以证明，对于  。因此在  的  个“花瓣”中，我们找到了两个比较特殊的：  ，它们的特殊性体现在上述映射下的性质。上面的讨论可以总结为下图：

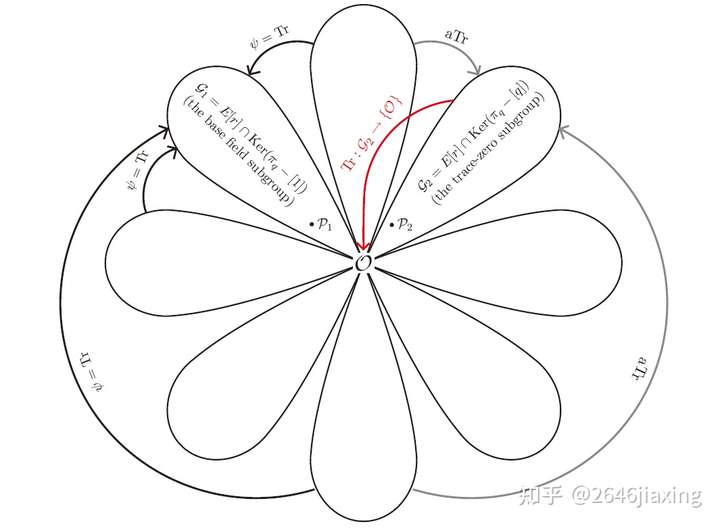
其中还有关于anti-Trace的性质，可参考上图，这里先不证明。

到此，我们已经找到了  中两个特殊的群，其实这两个群就是pairing所基于的两个群，但我们发现，  中的点的坐标是在扩域  上的，在实际应用中，往往取  ，这个扩域是非常大的，其上的计算也比较低效。因此，我们去找另一条曲线  ，使得它与原曲线  同构，既然同构，我们就可以将  上的  转化为  上某个点坐标在一个较小域上的子群，这样便可以提高计算效率，  上的这个子群就是我们真正的  。在下一节中，我们来介绍  和  的关系。

 

 

 

 

上节中，我们找到了  的  个花瓣中两个较为特殊的，即  ：

而且我们说明了 上述群写成 而非  的原因：因为  中点的坐标都是在扩域  中，其上的计算量大，导致pairing计算的效率也比较低，因此我们想找另一条曲线  ，使得它与原曲线  同构，利用这个同构关系，将  上的  转化为  上的与之同构的子群，这个子群中点的坐标在一个较小的域  上，因此，其上的计算会更快。我们称这样的曲线  为  的孪生曲线(twist curve)，或者叫扭曲线。

设  ，定义  ，其中  ，则  同构（这个可以参考介绍椭圆曲线理论的相关教材）。同构映射为：

，所谓两条曲线在  上同构，是指这两条曲线的群结构是同构的，即  ，既然  具有“花瓣”结构，因此  同样具有“花瓣”结构，因此，利用这个同构映射，便可将  上的转化为  上的某个子群。我们希望的是转化到某个点坐标在较小域  上的子群，然而，我们并不能使  任意小，我们当然希望  ，但有定理保证，  的取值只可能为  这几个值，显然最好的情况是  。下面我们通过一个简单的例子来说明：

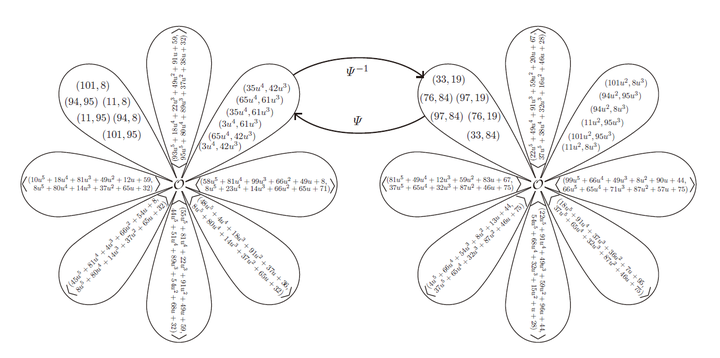
Example：设  ，  ，则  ，我们令  ，计算其嵌入次数  ，因此我们将域扩充至  ,利用不可约多项式  ，计算其孪生曲线  ，利用  之间的同构关系，我们有下图所示的转化：

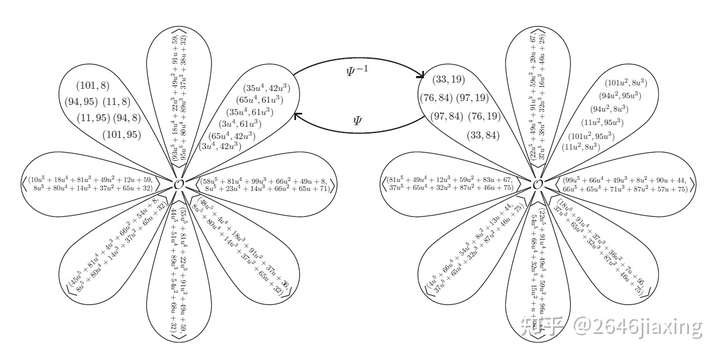
图中左侧表示  对应的群， 右侧表示 对应的群，左侧“花瓣”的左上角就是  ，右上角就是  ，利用同构映射，将  转化到了  上的子群，这个子群就是真正的  。我们将  转化到了一个点坐标在  上的子群，因此我们对应的是  的情况。

 

在国密算法SM9中所指定的曲线就是对应  的情况，其中  ，这条曲线属于BN曲线，BN曲线是一族曲线，其曲线参数都可以写成是关于某个变量的函数，这个变量取定一个值时，便生成一条曲线。

Pairing friendly curve：回忆之前的内容，我们每次都是选择一个素数  ，然后计算其嵌入次数  ，它是满足 的最小的正整数，之后就要将域扩张到  ，然后利用孪生曲线，最多可以将域降至  ，这里就有了这样的问题，如果  太大，即使除以6仍然会较大，这时pairing计算的效率也会很低，因此我们希望  一般较小，这样的曲线称为配对友好的曲线。我们将  可以写成  ，因此  是  在  中的阶，如果随机选择一条曲线的话，求出的  往往很大，故配对友好曲线需要用特殊的方法来寻找，而非随机生成一条曲线。