schnorr-signature

https://tlu.tarilabs.com/cryptography/digital_signatures/introduction_schnorr_signatures.html

数字签名

比特币使用数字签名使硬币能够在区块链上转移。数字签名用于证明特定硬币的所有权，并授权将其转移给新的所有者。

我们将电子硬币定义为数字签名链。每个所有者通过数字签名上次交易的哈希值和下一个所有者的公钥，将硬币转移到下一个。

–中本聪（Satoshi Nakamoto）在比特币白皮书（2008）中解释了UTXO模型。

当前，比特币使用椭圆曲线数字签名算法（ECDSA）。随着Taproot的升级，比特币将集成Schnorr，Schnorr是具有多种优势的第二种签名方案。

➤了解有关Taproot升级的更多信息。

ECDSA

自比特币诞生以来，ECDSA已被用于保护比特币。选择ECDSA的原因是比特币，原因如下：

开源。ECDSA不受专利或版权保护，因此将其用于比特币没有法律问题。
经过充分测试。ECDSA在最初设计比特币时就广为人知并得到了应用，其安全性经过多年的测试已得到充分确立。
OpenSSL。ECDSA在OpenSSL中实现，OpenSSL是比特币使用的开放源代码加密库。这使得针对比特币的ECDSA实施更加简单。

但是，ECDSA也有Schnorr改进的几个缺点。因此，开发人员已决定比特币应实施其他签名方案Schnorr。

Schnorr签名的优点

与ECDSA一样，Schnorr数字签名方案也使用椭圆曲线密码术（ECC）。在计算效率，存储和隐私方面，Schnorr签名提供了优于ECDSA的多个优势。

密钥和签名聚合

Schnorr签名提供的最显着优势是密钥聚合。典型的数字签名包含单个公共密钥，要签名的消息和签名，声称公共密钥的所有者对给定消息进行了签名。当多方希望对同一条消息进行签名（例如，通过多签名地址进行支出）时，它们各自必须包括其公共密钥和签名。因此，如果三个方要签名相同的消息，则证明将包括三个公钥和三个签名。由于计算和存储原因，这不是最佳选择，因为每个节点必须执行签名验证（一项昂贵的功能）三次，并存储三组签名和公钥。

密钥聚合消除了对多个公共密钥和签名的需求。可以对Schnorr公钥和签名进行汇总，这样，如果三个方要签署交易，则他们可以不信任地组合其三个公钥以形成单个公钥。然后，使用他们的三个私钥中的每一个，他们都可以签名同一条消息。最后，他们可以将其三个签名组合在一起以形成对聚合公钥有效的单个签名。验证者必须仅验证单个签名和公共密钥，以确保所有三个方都对消息进行了签名。

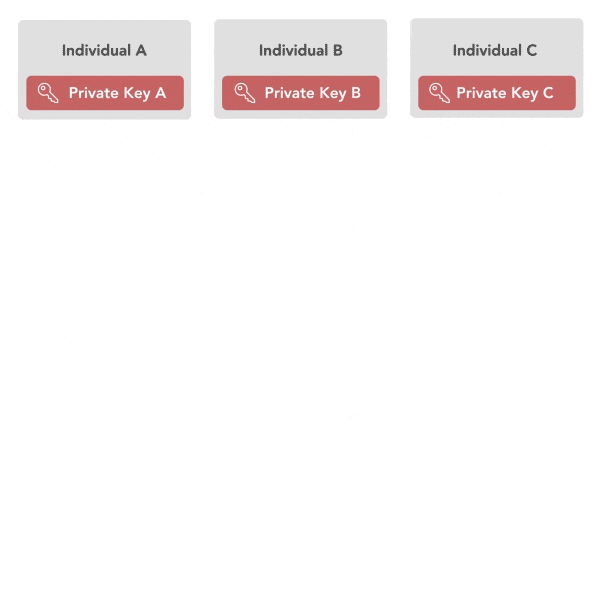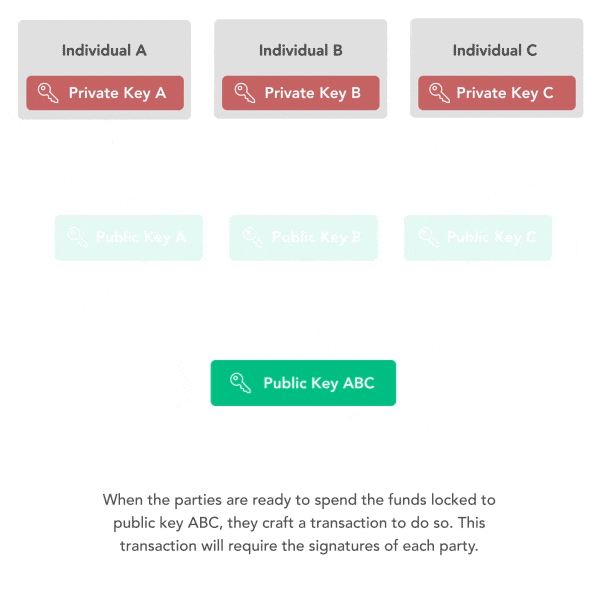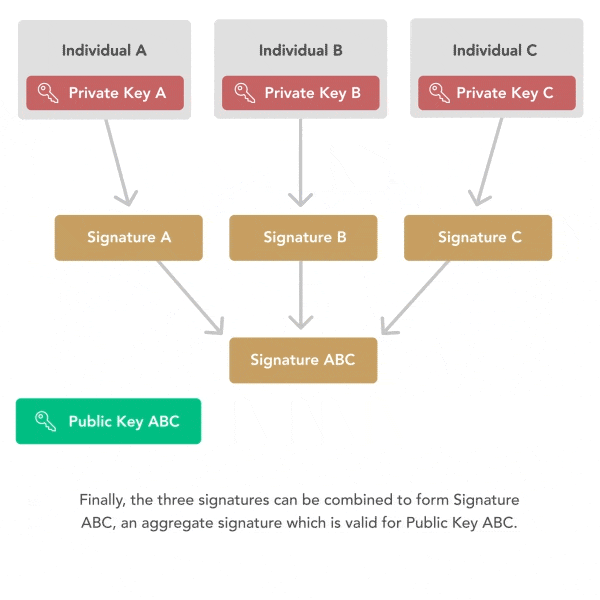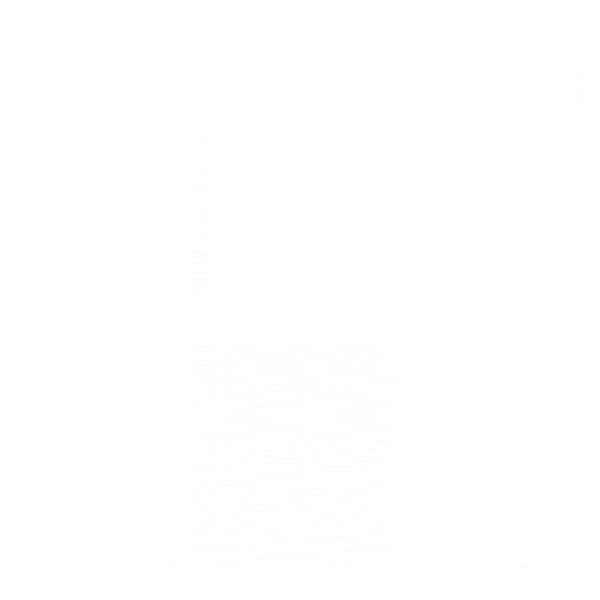
可以聚合Schnorr公共密钥和签名，以便可以将多个公共密钥组合为单个密钥，并且可以将来自那些公共密钥的多个签名聚合为对聚合的公共密钥有效的单个签名。

密钥聚合的隐私意义重大。由于多方可以聚合密钥和签名，因此多重签名交易可以完美地类似于单一签名交易。因此，所有Schnorr支出将彼此相似，因此链分析无法区分多重签名支出和单一签名支出。这将使链分析使用的几种启发式方法无效，包括常见的输入所有权启发式方法和脚本类型启发式方法。此隐私保护将扩展到所有使用Schnorr的比特币用户，但不扩展到使用ECDSA交易类型的比特币用户。

批量验证

节点收到新块时，通常会逐个验证该块中的每个事务和签名。这是一个耗时且资源密集的过程。

密钥聚合使比特币节点可以批量验证签名。这种方法大大减少了验证具有多个输入的事务所需的时间和计算能力。

由于Taproot是一个软叉子，即使激活Schnorr，大多数比特币用户和钱包仍将继续使用ECDSA。数据块将继续具有Schnorr签名和ECDSA签名，从而在短期内限制了批量验证的好处。

为什么比特币较早不使用Schnorr？

自1990年以来，Schnorr签名就一直受到专利保护，这严重限制了它们的使用并扼杀了创新。由于ECDSA是开源的，因此被广泛使用，经过严格测试并值得信赖。尽管Schnorr专利于2008年到期，但在同一年发明了比特币，但该决定认为Schnorr签名缺乏保护像比特币一样重要的系统所需的普及性和测试。

Schnorr签名将通过Taproot升级引入比特币，该升级有望在2022年左右启动。尽管开发人员已将所有必需的代码添加到Bitcoin Core，但比特币节点必须接受升级才能认为Schnorr签名有效。

Introduction to Schnorr Signatures

Overview

Private-public key pairs are the cornerstone of much of the cryptographic security underlying everything from secure web browsing to banking to cryptocurrencies. Private-public key pairs are asymmetric. This means that given one of the numbers (the private key), it's possible to derive the other one (the public key). However, doing the reverse is not feasible. It's this asymmetry that allows one to share the public key, uh, publicly and be confident that no one can figure out our private key (which we keep very secret and secure).

Asymmetric key pairs are employed in two main applications:

in authentication, where you prove that you have knowledge of the private key; and
in encryption, where messages can be encoded and only the person possessing the private key can decrypt and read the message.

In this introduction to digital signatures, we'll be talking about a particular class of keys: those derived from elliptic curves. There are other asymmetric schemes, not least of which are those based on products of prime numbers, including RSA keys [1].

We're going to assume you know the basics of elliptic curve cryptography (ECC). If not, don't stress, there's a gentle introduction in a previous chapter.

Let's get Started

This is an interactive introduction to digital signatures. It uses Rust code to demonstrate some of the ideas presented here, so you can see them at work. The code for this introduction uses the libsecp256k-rs library.

That's a mouthful, but secp256k1 is the name of the elliptic curve that secures a lot of things in many cryptocurrencies' transactions, including Bitcoin.

This particular library has some nice features. We've overridden the + (addition) and * (multiplication) operators so that the Rust code looks a lot more like mathematical formulae. This makes it much easier to play with the ideas we'll be exploring.

WARNING! Don't use this library in production code. It hasn't been battle-hardened, so use this one in production instead.

Basics of Schnorr Signatures

Public and Private Keys

The first thing we'll do is create a public and private key from an elliptic curve.

On secp256k1, a private key is simply a scalar integer value between 0 and ~2²⁵⁶. That's roughly how many atoms there are in the universe, so we have a big sandbox to play in.

We have a special point on the secp256k1 curve called G, which acts as the "origin". A public key is calculated by adding G on the curve to itself, $k_{a}$

P a = k a G

Let's take an example from this post, where it is known that the public key for 1, when written in uncompressed format, is 0479BE667...C47D08FFB10D4B8. The following code snippet demonstrates this:

extern crate libsecp256k1_rs;

use libsecp256k1_rs::{ SecretKey, PublicKey };

#[allow(non_snake_case)]
fn main() {
    // Create the secret key "1"
    let k = SecretKey::from_hex("0000000000000000000000000000000000000000000000000000000000000001").unwrap();
    // Generate the public key, P = k.G
    let pub_from_k = PublicKey::from_secret_key(&k);
    let known_pub = PublicKey::from_hex("0479BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8").unwrap();
    // Compare it to the known value
    assert_eq!(pub_from_k, known_pub);
    println!("Ok")
}

Creating a Signature

Approach Taken

Reversing ECC math multiplication (i.e. division) is pretty much infeasible when using properly chosen random values for your scalars ([5],[6]). This property is called the Discrete Log Problem, and is used as the principle behind many cryptography and digital signatures. A valid digital signature is evidence that the person providing the signature knows the private key corresponding to the public key with which the message is associated, or that they have solved the Discrete Log Problem.

The approach to creating signatures always follows this recipe:

Generate a secret once-off number (called a nonce), $r$
Create a public key, $R$
Send the following to Bob, your recipient - your message ( $m$

The actual signature is created by hashing the combination of all the public information above to create a challenge, $e$

e = H (R | | P | | m)

The hashing function is chosen so that e has the same range as your private keys. In our case, we want something that returns a 256-bit number, so SHA256 is a good choice.

Now the signature is constructed using your private information:

s = r + k e

Bob can now also calculate $e$

Note: When you construct the signature like this, it's known as a Schnorr signature, which is discussed in a following section. There are other ways of constructing $s$

But see this:

s G = (r + k e) G

Multiply out the right-hand side:

s G = r G + (k G) e

Substitute $R = r G$

s G = R + P e

So Bob must just calculate the public key corresponding to the signature $(s . G)$

Why do we Need the Nonce?

Why do we need a nonce in the standard signature?

Let's say we naïvely sign a message $m$

e = H (P | | m)

$e$

Now as before, we can check that the signature is valid:

s G = e k G = e (k G) = e P

$e$

We can show that leaving off the nonce is indeed highly insecure:

extern crate libsecp256k1_rs as secp256k1;

use secp256k1::{SecretKey, PublicKey, thread_rng, Message};
use secp256k1::schnorr::{ Challenge};

#[allow(non_snake_case)]
fn main() {
    // Create a random private key
    let mut rng = thread_rng();
    let k = SecretKey::random(&mut rng);
    println!("My private key: {}", k);
    let P = PublicKey::from_secret_key(&k);
    let m = Message::hash(b"Meet me at 12").unwrap();
    // Challenge, e = H(P || m)
    let e = Challenge::new(&[&P, &m]).as_scalar().unwrap();

    // Signature
    let s = e * k;

    // Verify the signature
    assert_eq!(PublicKey::from_secret_key(&s), e*P);
    println!("Signature is valid!");
    // But let's try calculate the private key from known information
    let hacked = s * e.inv();
    assert_eq!(k, hacked);
    println!("Hacked key:     {}", k)
}

ECDH

How do parties that want to communicate securely generate a shared secret for encrypting messages? One way is called the Elliptic Curve Diffie-Hellman exchange (ECDH), which is a simple method for doing just this.

ECDH is used in many places, including the Lightning Network during channel negotiation [3].

Here's how it works. Alice and Bob want to communicate securely. A simple way to do this is to use each other's public keys and calculate

extern crate libsecp256k1_rs as secp256k1;

use secp256k1::{ SecretKey, PublicKey, thread_rng, Message };

#[allow(non_snake_case)]
fn main() {
    let mut rng = thread_rng();
    // Alice creates a public-private keypair
    let k_a = SecretKey::random(&mut rng);
    let P_a = PublicKey::from_secret_key(&k_a);
    // Bob creates a public-private keypair
    let k_b = SecretKey::random(&mut rng);
    let P_b = PublicKey::from_secret_key(&k_b);
    // They each calculate the shared secret based only on the other party's public information
    // Alice's version:
    let S_a = k_a * P_b;
    // Bob's version:
    let S_b = k_b * P_a;

    assert_eq!(S_a, S_b, "The shared secret is not the same!");
    println!("The shared secret is identical")
}

For security reasons, the private keys are usually chosen at random for each session (you'll see the term ephemeral keys being used), but then we have the problem of not being sure the other party is who they say they are (perhaps due to a man-in-the-middle attack [4]).

Various additional authentication steps can be employed to resolve this problem, which we won't get into here.

Schnorr Signatures

If you follow the crypto news, you'll know that that the new hotness in Bitcoin is Schnorr Signatures.

But in fact, they're old news! The Schnorr signature is considered the simplest digital signature scheme to be provably secure in a random oracle model. It is efficient and generates short signatures. It was covered by U.S. Patent 4,995,082, which expired in February 2008 [7].

So why all the Fuss?

What makes Schnorr signatures so interesting and potentially dangerous, is their simplicity. Schnorr signatures are linear, so you have some nice properties.

Elliptic curves have the multiplicative property. So if you have two scalars $x, y$

(x + y) G = x G + y G = X + Y

$e$

You saw this property in a previous section, when we were verifying the signature. Schnorr signatures' linearity makes it very attractive for, among others:

signature aggregation;
atomic swaps;
"scriptless" scripts.

Naïve Signature Aggregation

Let's see how the linearity property of Schnorr signatures can be used to construct a two-of-two multi-signature.

Alice and Bob want to cosign something (a Tari transaction, say) without having to trust each other; i.e. they need to be able to prove ownership of their respective keys, and the aggregate signature is only valid if both Alice and Bob provide their part of the signature.

Assuming private keys are denoted $k_{i}$

P a g g e s a g g = P a + P b = H (R a

$e$

extern crate libsecp256k1_rs as secp256k1;

use secp256k1::{SecretKey, PublicKey, thread_rng, Message};
use secp256k1::schnorr::{Schnorr, Challenge};

#[allow(non_snake_case)]
fn main() {
    // Alice generates some keys
    let (ka, Pa, ra, Ra) = get_keyset();
    // Bob generates some keys
    let (kb, Pb, rb, Rb) = get_keyset();
    let m = Message::hash(b"a multisig transaction").unwrap();
    // The challenge uses both nonce public keys and private keys
    // e = H(Ra || Rb || Pa || Pb || H(m))
    let e = Challenge::new(&[&Ra, &Rb, &Pa, &Pb, &m]).as_scalar().unwrap();
    // Alice calculates her signature
    let sa = ra + ka * e;
    // Bob calculates his signature
    let sb = rb + kb * e;
    // Calculate the aggregate signature
    let s_agg = sa + sb;
    // S = s_agg.G
    let S = PublicKey::from_secret_key(&s_agg);
    // This should equal Ra + Rb + e(Pa + Pb)
    assert_eq!(S, Ra + Rb + e*(Pa + Pb));
    println!("The aggregate signature is valid!")
}

#[allow(non_snake_case)]
fn get_keyset() -> (SecretKey, PublicKey, SecretKey, PublicKey) {
    let mut rng = thread_rng();
    let k = SecretKey::random(&mut rng);
    let P = PublicKey::from_secret_key(&k);
    let r = SecretKey::random(&mut rng);
    let R = PublicKey::from_secret_key(&r);
    (k, P, r, R)
}

But this scheme is not secure!

Key Cancellation Attack

Let's take the previous scenario again, but this time, Bob knows Alice's public key and nonce ahead of time, by waiting until she reveals them.

Now Bob lies and says that his public key is $P_{b}^{'} = P_{b} - P_{a}$

Note that Bob doesn't know the private keys for these faked values, but that doesn't matter.

Everyone assumes that $s_{a g g} = R_{a} + R_{b}^{'} + e (P_{a} + P_{b}^{'})$

But Bob can create this signature himself:

s a g g G ∴ s a g g = R a + R' b + e (P a +

extern crate libsecp256k1_rs as secp256k1;

use secp256k1::{SecretKey, PublicKey, thread_rng, Message};
use secp256k1::schnorr::{Schnorr, Challenge};

#[allow(non_snake_case)]
fn main() {
    // Alice generates some keys
    let (ka, Pa, ra, Ra) = get_keyset();
    // Bob generates some keys as before
    let (kb, Pb, rb, Rb) = get_keyset();
    // ..and then publishes his forged keys
    let Pf = Pb - Pa;
    let Rf = Rb - Ra;

    let m = Message::hash(b"a multisig transaction").unwrap();
    // The challenge uses both nonce public keys and private keys
    // e = H(Ra || Rb' || Pa || Pb' || H(m))
    let e = Challenge::new(&[&Ra, &Rf, &Pa, &Pf, &m]).as_scalar().unwrap();

    // Bob creates a forged signature
    let s_f = rb + e * kb;
    // Check if it's valid
    let sG = Ra + Rf + e*(Pa + Pf);
    assert_eq!(sG, PublicKey::from_secret_key(&s_f));
    println!("Bob successfully forged the aggregate signature!")
}

#[allow(non_snake_case)]
fn get_keyset() -> (SecretKey, PublicKey, SecretKey, PublicKey) {
    let mut rng = thread_rng();
    let k = SecretKey::random(&mut rng);
    let P = PublicKey::from_secret_key(&k);
    let r = SecretKey::random(&mut rng);
    let R = PublicKey::from_secret_key(&r);
    (k, P, r, R)
}

Better Approaches to Aggregation

In the Key Cancellation Attack, Bob didn't know the private keys for his published $R$

This works, but it requires another round of messaging between parties, which is not conducive to a great user experience.

A better approach would be one that incorporates one or more of the following features:

It must be provably secure in the plain public-key model, without having to prove knowledge of secret keys, as we might have asked Bob to do in the naïve approach.
It should satisfy the normal Schnorr equation, i.e. the resulting signature can be verified with an expression of the form $R + e X$
It allows for Interactive Aggregate Signatures (IAS), where the signers are required to cooperate.
It allows for Non-interactive Aggregate Signatures (NAS), where the aggregation can be done by anyone.
It allows each signer to sign the same message, $m$
It allows each signer to sign their own message, $m_{i}$

MuSig

MuSig is a recently proposed ([8],[9]) simple signature aggregation scheme that satisfies all of the properties in the preceding section.

MuSig Demonstration

We'll demonstrate the interactive MuSig scheme here, where each signatory signs the same message. The scheme works as follows:

Each signer has a public-private key pair, as before.
Each signer shares a commitment to their public nonce (we'll skip this step in this demonstration). This step is necessary to prevent certain kinds of rogue key attacks [10].
Each signer publishes the public key of their nonce, $R_{i}$
Everyone calculates the same "shared public key", $X$

ℓ a i X = H (X 1 | | \dots | | X n) = H (ℓ

Note that in the preceding ordering of public keys, some deterministic convention should be used, such as the lexicographical order of the serialized keys.

Everyone also calculates the shared nonce, $R = \sum R_{i}$
The challenge, $e$
Each signer provides their contribution to the signature as:

s i = r i + k i a i e

Notice that the only departure here from a standard Schnorr signature is the inclusion of the factor $a_{i}$

The aggregate signature is the usual summation, $s = \sum s_{i}$

Verification is done by confirming that as usual:

s G \equiv R + e X

$e$

s G ◼ = \sum s i G = \sum (r i + k i a i e) G

$e$

extern crate libsecp256k1_rs as secp256k1;

use secp256k1::{ SecretKey, PublicKey, thread_rng, Message };
use secp256k1::schnorr::{ Challenge };

#[allow(non_snake_case)]
fn main() {
    let (k1, X1, r1, R1) = get_keys();
    let (k2, X2, r2, R2) = get_keys();
    let (k3, X3, r3, R3) = get_keys();

    // I'm setting the order here. In general, they'll be sorted
    let l = Challenge::new(&[&X1, &X2, &X3]);
    // ai = H(l || p)
    let a1 = Challenge::new(&[ &l, &X1 ]).as_scalar().unwrap();
    let a2 = Challenge::new(&[ &l, &X2 ]).as_scalar().unwrap();
    let a3 = Challenge::new(&[ &l, &X3 ]).as_scalar().unwrap();
    // X = sum( a_i X_i)
    let X = a1 * X1 + a2 * X2 + a3 * X3;

    let m = Message::hash(b"SomeSharedMultiSigTx").unwrap();

    // Calc shared nonce
    let R = R1 + R2 + R3;

    // e = H(R || X || m)
    let e = Challenge::new(&[&R, &X, &m]).as_scalar().unwrap();


    // Signatures
    let s1 = r1 + k1 * a1 * e;
    let s2 = r2 + k2 * a2 * e;
    let s3 = r3 + k3 * a3 * e;
    let s = s1 + s2 + s3;

    //Verify
    let sg = PublicKey::from_secret_key(&s);
    let check = R + e * X;
    assert_eq!(sg, check, "The signature is INVALID");
    println!("The signature is correct!")
}

#[allow(non_snake_case)]
fn get_keys() -> (SecretKey, PublicKey, SecretKey, PublicKey) {
    let mut rng = thread_rng();
    let k = SecretKey::random(&mut rng);
    let P = PublicKey::from_secret_key(&k);
    let r = SecretKey::random(&mut rng);
    let R = PublicKey::from_secret_key(&r);
    (k, P, r, R)
}

Security Demonstration

As a final demonstration, let's show how MuSig defeats the cancellation attack from the naïve signature scheme. Using the same idea as in the Key Cancellation Attack section, Bob has provided fake values for his nonce and public keys:

R f X f = R b - R a = X b - X a

$e$

ℓ a a a f X R e = H (X a | | X f) = H

$e$

s b = r b + k s e

$e$

s b G (r b + k s e) G k s e k s = R + e X =

$e$

Replay Attacks!

It's critical that a new nonce be chosen for every signing ceremony. The best way to do this is to make use of a cryptographically secure (pseudo-)random number generator (CSPRNG).

But even if this is the case, let's say an attacker can trick us into signing a new message by "rewinding" the signing ceremony to the point where partial signatures are generated. At this point, the attacker provides a different message, $e^{'} = H (. . . | | m^{'})$

s' i = r i + a i k i e'

$e$

s' i - s i ∴ k i = (r i + a i k i e') - (r i + a i

$e$

References

[1] Wikipedia: "RSA (Cryptosystem)" [online]. Available: https://en.wikipedia.org/wiki/RSA_(cryptosystem). Date accessed: 2018‑10‑11.

[2] Wikipedia: "Elliptic Curve Digital Signature Algorithm" [online]. Available: https://en.wikipedia.org/wiki/Elliptic_Curve_Digital_Signature_Algorithm. Date accessed: 2018‑10‑11.

[3] Github: "BOLT #8: Encrypted and Authenticated Transport, Lightning RFC" [online].
Available: https://github.com/lightningnetwork/lightning-rfc/blob/master/08-transport.md. Date accessed: 2018‑10‑11.

[4] Wikipedia: "Man in the Middle Attack" [online]. Available: https://en.wikipedia.org/wiki/Man-in-the-middle_attack. Date accessed: 2018‑10‑11.

[5] StackOverflow: "How does a Cryptographically Secure Random Number Generator Work?" [online]. Available: https://stackoverflow.com/questions/2449594/how-does-a-cryptographically-secure-random-number-generator-work. Date accessed: 2018‑10‑11.

[6] Wikipedia: "Cryptographically Secure Pseudorandom Number Generator" [online]. Available: https://en.wikipedia.org/wiki/Cryptographically_secure_pseudorandom_number_generator. Date accessed: 2018‑10‑11.

[7] Wikipedia: "Schnorr Signature" [online]. Available: https://en.wikipedia.org/wiki/Schnorr_signature. Date accessed: 2018‑09‑19.

[8] Blockstream: "Key Aggregation for Schnorr Signatures" [online]. Available: https://blockstream.com/2018/01/23/musig-key-aggregation-schnorr-signatures.html. Date accessed: 2018‑09‑19.

[9] G. Maxwell, A. Poelstra, Y. Seurin and P. Wuille, "Simple Schnorr Multi-signatures with Applications to Bitcoin" [online]. Available: https://eprint.iacr.org/2018/068.pdf. Date accessed: 2018‑09‑19.

[10] M. Drijvers, K. Edalatnejad, B. Ford, E. Kiltz, J. Loss, G. Neven and I. Stepanovs, "On the Security of Two-round Multi-signatures", Cryptology ePrint Archive, Report 2018/417 [online]. Available: https://eprint.iacr.org/2018/417.pdf. Date accessed: 2019‑02‑21.

Contributors

posted @ 2021-02-05 16:18 zJanly 阅读(466) 评论(0) 编辑收藏举报

刷新页面返回顶部