A bilinear pairing is a map

A bilinear pairing is a map e : G1 × G2 → G3 where G1, G2 are additive groups, G3 is a multiplicative group, and the map is linear in each component: e(P + Q, R) = e(P, R) · e(Q, R) e(P, Q + R) = e(P, Q) · e(P, R).

 

 

 

 

 

Explaining SNARKs Part VII: Pairings of Elliptic Curves

Ariel Gabizon | 

June 7, 2017

<< Part VI

In Part VI, we saw an outline of the Pinocchio zk-SNARK. We were missing two things – an HH that supports both addition and multiplication that is needed for the verifier’s checks, and a transition from an interactive protocol to a non-interactive proof system.

In this post we will see that using elliptic curves we can obtain a limited, but sufficient for our purposes, form of HH that supports multiplication. We will then show that this limited HH also suffices to convert our protocol to the desired non-interactive system.

We begin by introducing elliptic curves and explaining how they give us the necessary HH.

Elliptic curves and their pairings

Assume $\mathrm{p is\; a\; prime\; larger\; than 3,\; and\; take\; some u,v\in Fp such\; that 4u3+27v2\ne 0.\; We\; look\; at\; the\; equation}$

${\mathrm{Y2=X3+u\cdot X+v}}^{}$

An elliptic curve $\mathrm{C is\; the\; of\; set\; of\; points (x,y) [1] that\; satisfy\; such\; an\; equation.\; These\; curves\; give\; us\; an\; interesting\; way\; to\; construct\; groups.\; The\; group\; elements\; will\; be\; the\; points (x,y)\in F2p that\; are\; on\; the\; curve,\; i.e.,\; that\; satisfy\; the\; equation,\; together\; with\; a\; special\; point O,\; that\; for\; technical\; reasons\; is\; sometimes\; refered\; to\; as\; the\; “point\; at\; infinity”,\; and\; serves\; as\; the\; identity\; element,\; i.e.\; the\; zero\; of\; the\; group.}$

Now the question is how we add two points $\mathrm{P=(x1,y1),Q=(x2,y2) to\; get\; a\; third?\; The\; addition\; rule\; is\; derived\; from\; a\; somewhat\; abstract\; object\; called\; the divisor\; class\; group of\; the\; curve.\; For\; our\; purposes,\; all\; you\; have\; to\; know\; about\; this\; divisor\; class\; group\; is\; that\; it\; imposes\; the\; following\; constraint\; on\; the\; definition\; of\; addition:\; The\; sum\; of\; points\; on\; any\; line\; must\; be\; zero,\; i.e., O.}$

Let’s see how the addition rule is derived from this constraint. Look at a vertical line, defined by an equation of the form $\mathrm{X=c.\; Suppose\; this\; line\; intersects\; the\; curve\; at\; a\; point P=(x1,y1).\; Because\; the\; curve\; equation\; is\; of\; the\; form Y2=f(X),\; if (x1,y1) is\; on\; the\; curve,\; so\; is\; the\; point Q:=(x1,-y1).\; Moreover,\; since\; it’s\; a\; vertical\; line\; and\; the\; curve\; equation\; is\; of\; degree\; two\; in Y,\; we\; can\; be\; sure\; these\; are\; the\; only\; points\; where\; the\; line\; and\; curve\; intersect.}$

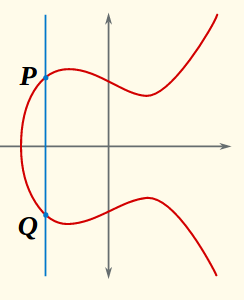
Thus, we must have $\mathrm{P+Q=O which\; means P=-Q;\; that\; is, Q is\; the\; inverse\; of P in\; the\; group.}$

Now let us look at points $\mathrm{P and Q that\; have\; a\; different\; first\; coordinate\; –\; that\; is, x1\ne x2,\; and\; see\; how\; to\; add\; them.\; We\; pass\; a\; line\; through P and Q.}$

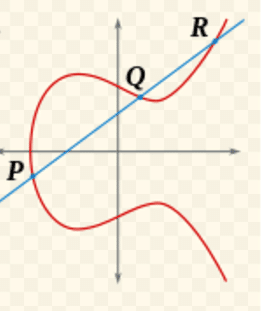
Since the curve is defined by a degree three polynomial in $\mathrm{X and\; already\; intersects\; this\; (non-vertical)\; line\; at\; two\; points,\; it\; is\; guaranteed\; to\; intersect\; the\; line\; at\; a\; third\; point,\; that\; we\; denote R=(x,y),\; and\; no\; other\; points.}$

So we must have $\mathrm{P+Q+R=O,\; which\; means P+Q=-R;\; and\; we\; know\; by\; now\; that -R is\; obtained\; from R by\; flipping\; the\; second\; coordinate\; from y to -y.}$

Thus, we have derived the addition rule for our group: Given points $\mathrm{P and Q,\; pass\; a\; line\; through\; them,\; and\; then\; take\; the\; “mirror”\; point\; of\; the\; third\; intersection\; point\; of\; the\; line\; as\; the\; addition\; result. [2]}$

This group is usually called $\mathrm{C(Fp) –\; as\; it\; consists\; of\; points\; on\; the\; curve C with\; coordinates\; in Fp;\; but\; let’s\; denote\; it\; by G1 from\; now\; on.\; Assume\; for\; simplicity\; that\; the\; number\; of\; elements\; in G1 is\; a\; prime\; number r,\; and\; is\; different\; from p.\; This\; is\; many\; times\; the\; case,\; for\; example\; in\; the\; curve\; that\; Zcash\; is\; currently\; using.\; In\; this\; case,\; any\; element g\in G1 different\; from O generates G1.}$

The smallest integer $\mathrm{k such\; that r divides pk-1 is\; called\; the embedding\; degree of\; the\; curve.\; It\; is\; conjectured\; that\; when k is\; not\; too\; small,\; say,\; at\; least 6,\; then\; the\; discrete\; logarithm\; problem\; in G1,\; i.e.\; finding \alpha from g and \alpha \cdot g,\; is\; very\; hard.\; (In\; BN\; curves [3] currently\; used\; by\; Zcash k=12.)}$

The multiplicative group of ${\mathrm{Fpk contains\; a\; subgroup\; of\; order r that\; we\; denote GT.\; We\; can\; look\; at\; curve\; points\; with\; coordinates\; in Fpk and\; not\; just\; in Fp.\; Under\; the\; same\; addition\; rule,\; these\; points\; also\; form\; a\; group\; together\; with O called C(Fpk).\; Note\; that C(Fpk) clearly\; contains G1.\; Besides G1, C(Fpk) will\; contain\; an\; additional\; subgroup G2 of\; order r (in\; fact, r-1 additional\; subgroups\; of\; order r).}}^{}$

Fix generators $\mathrm{g\in G1,h\in G2.\; It\; turns\; out\; that\; there\; is\; an\; efficient\; map,\; called\; the Tate\; reduced\; pairing,\; taking\; a\; pair\; of\; elements\; from G1 and G2 into\; an\; element\; of GT,}$

such that

1. $\mathrm{Tate(g,h)=g for\; a\; generator g of GT,\; and}$
2. given a pair of elements $\mathrm{a,b\in Fr,\; we\; have Tate(a\cdot g,b\cdot h)=gab.}$

Defining $\mathrm{Tate is\; a\; bit\; beyond\; the\; scope\; of\; this\; series,\; and\; relies\; on\; concepts\; from\; algebraic\; geometry,\; most\; prominently\; that\; of divisors.\; Here’s\; a\; sketch\; of Tate’s\; definition: [4]}$

For $\mathrm{a\in Fp the\; polynomial (X-a)r has\; a\; zero\; of\; multiplicity r at\; the\; point a,\; and\; no\; other\; zeroes.\; For\; a\; point P\in G1,\; divisors\; enable\; us\; to\; prove\; there\; exists\; a\; function fP from\; the\; curve\; to Fp that\; also\; has,\; in\; some\; precise\; sense,\; a\; zero\; of\; multiplicity r at P and\; no\; other\; zeroes. Tate(P,Q) is\; then\; defined\; as fP(Q)(pk-1)/r.}$

It may not seem at all clear what this definition has to do with the stated properties, and indeed the proof that $\mathrm{Tate has\; these\; properties\; is\; quite\; complex.}$

Defining ${\mathrm{E1(x):=x\cdot g,E2(x):=x\cdot h,E(x):=x\cdot g,\; we\; get\; a\; weak\; version\; of\; an\; HH\; that\; supports\; both\; addition\; and\; multiplication: E1,E2,E are\; HHs\; that\; support\; addition,\; and\; given\; the\; hidings E1(x), E2(y) we\; can\; compute E(xy).\; In\; other\; words,\; if\; we\; have\; the\; ”right”\; hidings\; of x and y we\; can\; get\; a\; (different)\; hiding\; of xy.\; But\; for\; example,\; if\; we\; had\; hidings\; of x,y,zwe\; couldn’t\; get\; a\; hiding\; of xyz.}}^{}$

We move on to discussing non-interactive proof systems. We begin by explaining exactly what we mean by ‘non-interactive’.

Non-interactive proofs in the common reference string model

The strongest and most intuitive notion of a non-interactive proof is probably the following. In order to prove a certain claim, a prover broadcasts a single message to all parties, with no prior communication of any kind; and anyone reading this message would be convinced of the prover’s claim. This can be shown to be impossible in most cases. [5]

A slightly relaxed notion of non-interactive proof is to allow a common reference string (CRS). In the CRS model, before any proofs are constructed, there is a setup phase where a string is constructed according to a certain randomized process and broadcast to all parties. This string is called the CRS and is then used to help construct and verify proofs. The assumption is that the randomness used in the creation of the CRS is not known to any party – as knowledge of this randomness might enable constructing proofs of false claims.

We will explain how in the CRS model we can convert the verifiable blind evaluation protocol of Part IV into a non-interactive proof system. As the protocol of Part VI consisted of a few such subprotocols it can be turned into a non-interactive proof system in a similar way.

A non-interactive evaluation protocol

The non-interactive version of the evaluation protocol basically consists of publishing Bob’s first message as the CRS. Recall that the purpose of the protocol is to obtain the hiding $\mathrm{E(P(s)) of\; Alice’s\; polynomial P at\; a\; randomly\; chosen s\in Fr.}$

Setup: Random $\mathrm{\alpha \in F\ast r,s\in Fr are\; chosen\; and\; the\; CRS:}$

$(E1(1),E1(s),\dots ,E1(sd), E2(\alpha ),E2(\alpha s),\dots ,E2(\alpha sd))$

is published.

Proof: Alice computes $\mathrm{a=E1(P(s)) and b=E2(\alpha P(S)) using\; the\; elements\; of\; the\; CRS,\; and\; the\; fact\; that E1 and E2support\; linear\; combinations.}$

Verification: Fix the $\mathrm{x,y\in Fr such\; that a=E1(x) and b=E2(y).\; Bob\; computes E(\alpha x)=Tate(E1(x),E2(\alpha )) and E(y)=Tate(E1(1),E2(y)),\; and\; checks\; that\; they\; are\; equal.\; (If\; they\; are\; equal\; it\; implies \alpha x=y.)}$

As explained in Part IV, Alice can only construct $\mathrm{a,b that\; will\; pass\; the\; verification\; check\; if a is\; the\; hiding\; of P(s) for\; a\; polynomial P of\; degree d known\; to\; her.\; The\; main\; difference\; here\; is\; that\; Bob\; does\; not\; need\; to\; know \alpha for\; the\; verification\; check,\; as\; he\; can\; use\; the\; pairing\; function\; to\; compute E(\alpha x) only\; from E1(x) and E2(\alpha ).\; Thus,\; he\; does\; not\; need\; to\; construct\; and\; send\; the\; first\; message\; himself,\; and\; this\; message\; can\; simply\; be\; fixed\; in\; the\; CRS.}$

[1]

You may ask ‘The set of points from where?’. We mean the set of points with coordinates in the algebraic closure of ${\mathrm{Fp.\; Also,\; the\; curve\; has\; an\; affine\; and\; projective\; version.\; When\; we\; are\; referring\; to\; the\; projective\; version\; we\; also\; include\; the\; “point\; at\; infinity” O as\; an\; element\; of\; the\; curve.}}^{}$

[2]	We did not address the case of adding $\mathrm{P to\; itself.\; This\; is\; done\; by\; using\; the\; line\; that\; is\; tangent\; to\; the\; curve\; at P,\; and\; taking R to\; be\; the\; second\; intersection\; point\; of\; this\; line\; with\; the\; curve.}$

[3]	https://eprint.iacr.org/2005/133.pdf

[4]	The pairing Zcash actually uses is the optimal Ate pairing, which is based on the Tate reduced pairing, and can be computed more efficiently than $\mathrm{Tate.}$

[5]

In computational complexity theory terms, one can show that only languages in BPP have non-interactive zero-knowledge proofs in this strong sense. The type of claims we need to prove in Zcash transactions, e.g. ‘I know a hash preimage of this string’, correspond to the complexity class NP which is believed to be much larger than BPP.

[6]	The images used were taken from the following article and are used under the creative commons license.

Technical

#

cryptography

, 

explainers

, 

zksnarks